#IjustWantContribution
It seems there isn't any blog about Berlekamp-Massey Algorithm around here, so I decided to go on a try. :P
Acknowledgement: Hats off to matthew99 for introducing this algorithm.
What is 'linear recurrence'?
Assuming there is a (probably infinity) sequence a0, a1...an - 1, we call this sequence satisfies a linear recurrence relation p1, p2...pm, iff 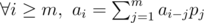 . (Obviously, if m ≥ n any p can do :P)
. (Obviously, if m ≥ n any p can do :P)
How to calculate k-th term of a linear recurrence?
For a polynomial 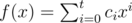 , we define
, we define 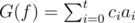 .
.
Obviously G satisfies G(f) ± G(g) = G(f ± g).
Because 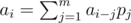 , if we let
, if we let 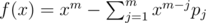 , then G(f) = 0. Also G(fx), G(fx2)... = 0. So G(fg) = 0 (g is any polynomial).
, then G(f) = 0. Also G(fx), G(fx2)... = 0. So G(fg) = 0 (g is any polynomial).
What we want is G(xk). Because G(f⌊ xk / f⌋) = 0, then 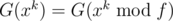 . We can calculate
. We can calculate  in a binary-exponentiation manner, then calculate
in a binary-exponentiation manner, then calculate 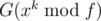 . Time complexity is
. Time complexity is 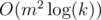 or
or 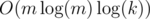 (if you use fft etc.)
(if you use fft etc.)
How to find (the shortest) linear recurrence relation?
It's Berlekamp-Massey Algorithm to the rescue! For a given sequence x0, x1...xn - 1, it can calculate one shortest linear recurrence relation for every prefix in O(n2) time.
Let's define the value of a relation sequence p1, p2...pm evaluated at position t:  (t ≥ m). A valid linear recurrence relation is a relation sequence with correct value evaluated at every position ≥ m.
(t ≥ m). A valid linear recurrence relation is a relation sequence with correct value evaluated at every position ≥ m.
Let's consider the numbers from left to right. Start from {}, we evaluate the current relation sequence at current position t (from 1 to n). If we got at, then it's still good, go on. Assume we've got value v, if we somehow got some relation sequence x that evaluated as 1 at position t, and evaluated as 0 (or undefined) at positions < t, then minus current sequence with (v - at)x, we're done.
If this is not first non-zero position, we have run into this situation before. Let's say s = {s1, s2...sm} evaluated as xt' + v' at position t' and correct at positions before t', then {1, - s1, - s2... - sm} should evaluated as v' at position t' + 1 and 0 otherwise. Divide it with v' and add proper (t - t' - 1) zeroes in front, we've got the x we need!
If we run into this situation several times before, we can choose the one that is shortest after filling zeroes.
Combine the above two section, we can acquire a handy weapon for these kind of problems :)
Because we need division, the modulus needs to be a prime.
Applications
Or, in other words, where can we find linear recurrences?
From the point of generating function, let A and P be the generating function of a and p, then A = AP + A0 (A0 depends on the first terms of a), then A = A0 / (1 - P). Moreover, if A = B / C and the constant term of C is 1 then there is a linear recurrence relation for a. So, provided with the generating function of a, one can tell if it's a linear recurrence easily.
If we have some kind of dynamic-programming f[i][j] (i ≤ n, j ≤ m), we want to find f[n][1]. The transitions of f is something like 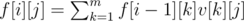 . In old days, we may use matrix-multiplications. But things have changed! Calculate f[1][1], f[2][1]...f[m + m + m][1] and plug in the above code, we're done!
. In old days, we may use matrix-multiplications. But things have changed! Calculate f[1][1], f[2][1]...f[m + m + m][1] and plug in the above code, we're done!
Why? Consider f[i] as a vector and v as a matrix, then f[i] = f[i - 1]v, so f[n] = f[1]vn - 1. Consider the minimal polynomial of v, it's degree must be ≤ m and obviously there's a corresponding linear recurrence relation with length ≤ m. With a prefix of length m + m + m it's enough to figure out a correct relation.
Why is it better than matrix multiplication? Besides it's  instead of
instead of 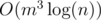 (after calculating f[1]...f[m+m+m], calculating might take O(m3) though), sometimes it's hard to acquire the exact transition matrix (or maybe just you're lazy enough), and this algorithm makes life better.
(after calculating f[1]...f[m+m+m], calculating might take O(m3) though), sometimes it's hard to acquire the exact transition matrix (or maybe just you're lazy enough), and this algorithm makes life better.
Try your hands
http://codeforces.com/contest/506/problem/E Write a naive dynamic-programming for small n, plug in BM, you're done! Life has never been so easy.
https://loj.ac/problem/2463 A chinese problem: Let n be a power of 2, you're given a directed graph with n nodes, from i to j there're Ai, j directed edges. Little Q is going on several trips, for every trip he will start from some node, make at least one step (i.e. go through at least one edge) and end at some node. He is wondering the number of ways if he's going on several travels, making x steps at total, and the bitwise-and of all start nodes and end nodes equals to y. For every 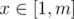 ,
, 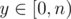 , you need to find the way modulo 998244353. To reduce output size, only output the bitwise-xor of all m × n answers. 2 ≤ n ≤ 64, 1 ≤ m ≤ 20000.
, you need to find the way modulo 998244353. To reduce output size, only output the bitwise-xor of all m × n answers. 2 ≤ n ≤ 64, 1 ≤ m ≤ 20000.
There're many more problems that can be solved in this way, but since posting them here is already spoiling I'm not going to post more :)











If the "contribution movement" is causing such great posts, please SMASH THAT LIKE BUTTON. Thanks!
Who cares about contribution points honestly?
They do these blogs cause they want to contribute to community, not because they want some contribution points. They're not that dumb.
MijPeter Did you even read the blog? "#IjustWantContribution" because this is the first sentence, jejejejejeje, just joking
It seems that your program doesn't work when the given modulo is NOT a prime. I've tested it on the sample of this problem: http://www.spoj.com/problems/FINDLR and it fails on the sample.
When modulo is not a prime, BM described in this article will not work, because modular inversion is needed. For example, when modulo 4, you cannot find a good linear recurrence relation for
2 1simply because there isn't a 1/2. I'm not sure about that problem though...Then could you please mention the condition when your program work in the main blog?
Well it won't work. I'll add the conditions.
For that problem, you can use Reeds–Sloane algorithm, which is an extension of BM for prime powers, and then combine the results with CRT.
Can you give a good reference of Reeds-Sloane or to do a blog of that algorithm. Thanks in advance.
You can refer to my implementation: linear-recurrence.cc.
zimpha Thanks, really. xd
Actually, I tried to solve SPOJ FINDLR using your implementation. But I could only manage Runtime Error. I am stuck in this for a couple of time, but cannot figure out where the bug is. Is it a bug in your implementation or I am getting something wrong ? I would appreciate your help a lot.
Here is my code.
Not sure about the Reeds-Sloane, but the BM has a weird bug when a0 is zero, since it tries to find its inverse and divide it by zero. It's different from what is described in the paper. The later deals with trailing zeroes just fine.
Hi there, zimpha. I can see that you actually had an AC submission in this problem (the only one as well). How did you fix the bug ? We would be very grateful if you did kindly share.
Thank you so much for this blog! Berlekamp-Massey is an algorithm that I always wanted to learn but was unable to due to the wikipedia page being hard to read, and google not turning up what I wanted to find.
Any reason why this is not on homepage while Blogewoosh is? Like what is the criteria for a post to be featured in the homepage?
Blogewoosh is supposed to be a series of blogs.
Ignore
I think we need a special section for this kind of blogs. The top section is almost good, but it also contains announces and other not related stuff
Totally agreed. This feature is a must have. I have seen multiple attempts to create a single blog post with good links but they are eventually abandoned.
I'm willing to help on this effort if Codeforces plans to move ahead with this feature.
OK. Now I maybe understand kostka's comment about existing editorial in Polish which is (in his opinion) better than Radewoosh's post.
I'm sorry, but your post is as incomprehensible as wiki article. The main reason for that article on wiki is hard to understand for us is that Berlekamp's algorithm initially was for BCH decoding and it was formulated in terms of Coding theory. But then Massey understood that this algorithm is applicable for solving arbitrary linear recurrences. His article is free and contains detailed proofs. AND IT IS IN ENGLISH. Like, readable English, you know.
I can't understand anything from your post. And I cannot see any excuses like in Berlekamp's case. Even code is not helping. If you are writing this code for others in order to help them understand some algorithm, how about using good variable naming, writing comments in substantial lines and use goddamn spaces? Maybe even make it slower, make everything as explicit as possible without changing complexity. For example, you say that this algorithm build answer for every prefix of the sequence. Why not store answer for each prefix? It is not bad for complexity.
Thanks to Merkurev who understood the algorithm after it was used in one of the problems in Petrozavodsk training camp and then shared Massey's article.
Feedback is a good thing, and I agree with most of your points. But for me, this seems too demanding from an article writer who already devoted a lot of times. Like, should he learn English because of this?
Btw, which contest in Petrozavodsk camp used this algorithm? I'm curious :p
Petrozavodsk winter 2018, ITMO contest (day 2), F
Thanks, is the problem available online? And if, can you please share the link?
No, Petrozavodsk contests usually are not available online. However, you can find this contest and a lot of others on opentrains. To register on this judge you should contact with snarknews.
I tried to explain things clearly. Anyway, my English is rather poor. I'll try if there's something that can be improved.
About the code, I just copy-pasted it from my own template, I'll try to make it clearer.
This race for contributions is very healthy. We are getting lots of informative blogs about algorithms and tricks. I think all red coders should do this.
Thank you TLE, Radewoosh and all others who are trying so hard.
As a Chinese high school student, I find the article much more readable than those in authentic English.Because all we Chinese high school students speak Chinglish in the same strange way :P
You've got it!
I didn't understand the how to calculate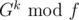 in
in 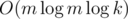 .
.
Can anyone explain how to calculate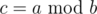 using FFT, if a and b are polynomials? Thought of the following way: calculate DFTs a' and b', then calculate c', where
using FFT, if a and b are polynomials? Thought of the following way: calculate DFTs a' and b', then calculate c', where  , then calculate c using inverse FFT. But what to do if b'i = 0 for some i?
, then calculate c using inverse FFT. But what to do if b'i = 0 for some i?
Here is a good lecture about polynomials, maybe it will help.
Thanks, I'll take a look on it
According to this lecture, the complexity should be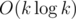 . How do you make it into
. How do you make it into 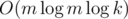 ?
?
As said in the post,
Yup, I read that. However, I can't find any way to do that. Can you help me elaborate the idea?
Use the same approach as if you want to calculate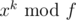 where x, k and f are just positive integers.
where x, k and f are just positive integers.
Suppose you have (quite simple to calculate). Then you want to calculate some
(quite simple to calculate). Then you want to calculate some 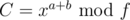 if you know
if you know 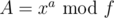 and
and 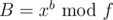 . It is just
. It is just 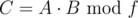 (like with integers). Using this, it's easy to exponentiate
(like with integers). Using this, it's easy to exponentiate  into power k.
into power k.
hahaha
Thanks for the acknowledgment :)
"Calculate f[1][1], f[2][1]...f[m + m + m][1]": I think, in general, it requires O(m3).
Generally yes. Even so it's still better than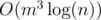 .
.
Also if the transition matrix is sparse then it might require less than $$$O(m^3)$$$, while matrix exponential would still be $$$O(m^2 \log(n))$$$.
For matrix exponentiation problems, why do you need 3m terms? Isn't 2m enough to uniquely determine all the coefficients of the linear recurrence?
Indeed, $$$2 \cdot m$$$ terms are enough.
$$$2m$$$ terms are indeed enough, I guess I was not so sure of the proof details when writing this blog.
Hello TLE it seems that in sample, for evaluation of 124 we should find a5-2a4-a3 instead of a4-2a3+a4
Why downvotes? Can anyone tell me whether this is right or wrong.
Fixed, thanks!