Hello CodeForces Community!
It’s time to gear up for CodeChef’s November Long Challenge sponsored by ShareChat! 10 days of coding fun plus opportunities to work at ShareChat! More details can be found on the contest page.
Joining me on the problem setting panel are:
- Admin: mgch (Misha Chorniy)
- Problem Tester: TLE (Zhong Ziqian)
- Editorialist: taran_1407 (Taranpreet Singh)
- Problem Setters: sunset (Xiuhan Wang), bciobanu (Bogdan Ciobanu), altruist (Denis Anishchenko), TLE (Zhong Ziqian), teja349 (Teja Vardhan Reddy), adamant (Alexander Kulkov), danya.smelskiy (Danya Smelskiy), Shivam Gupta, hm2 (Himanshu Mishra), sshhhh (Sumegh Roychowdhury)
- Statement Verifier: Xellos (Jakub Safin)
- Russian Translator: Mediocrity (Fedor Korobeinikov)
- Mandarin Translator: huzecong (Hu Zecong)
- Vietnamese Translator: VNOI Team
- Hindi Translator: Akash Srivastava
- Bengali Translator:solaimanope (Mohammad Solaiman)
I enjoy this set of problems personally and hope you will enjoy solving them too. You can give your feedback on the problem set in the comments below, after the contest.
Contest Details:
Time: 2nd November 2018 (1500 hrs) to 12th November (1500 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.
Contest link: www.codechef.com/NOV18
Registration: You just need to have a CodeChef handle to participate. For all those, who are interested and do not have a CodeChef handle, are requested to register in order to participate.
Prizes: Top 10 performers in Global and Indian category will get CodeChef laddus, with which the winners can claim cool CodeChef goodies. First to solve each problem except challenge — 100 laddus. Know more here.
(For those who have not yet got their previous winning, please send an email to [email protected])
Good Luck and Have Fun! Hope to see you participating!











How to solve Binary Strings ? I have some ideas with trie ,but it was difficult to implement .
Basically, if max(|AL|, |AL + 1|..|AR|) > |X|, you will try to choose among ones with max lengths. Furthermore, you will choose from the ones that maximize the prefix before X. If you insert all strings of that same length into a trie, this is just the rightmost node of that depth in that trie. To deal with that range restriction, you can use divide and conquer / scanning line and segment tree etc. The rest is just walking on the trie. If max(|AL|, |AL + 1|..|AR|) ≤ |X|, just walk on several tries.
i don't understand clearly ,how i can use segment tree TLE ?
UPD: Sorry for misleading but my old solution might be way too complicated.
For a query l, r, just consider the maximum of pair(length,string) (i.e. sort all same-lengthed strings and use sorted index). After finding that maximum, locate the correspondent trie node and you're done.
it is similar to MO algorithm ,am i right ?
Kind of.
thanks for your explanation TLE ! I will try to implement it.
I also implemented it with tries. Just insert all elements into the trie by making it of equal length(pad it with 0's) and compress it. Then for each query traverse the trie.
What do you mean by compress it? My approach was to build multiple tries in each node, and it passed, but this sounds interesting as well. Do you mean like merging a node with its child if it have only 1 child?
Yeah. Exactly just merge node and child if it is a single child. Initially add Max length amount of 0's and for each 0 store it's address in a map and access it for adding extra 0's(padding)
Can you explain your query part ?
Ok. For the query if the length of the string is greater than the length of strings on the trie (after padding all are of equal length) then take the substring of it and query it. Else if it is lesser then have a count of 0's that must be padded. Don't add the 0's to the query string as it may tle. Traverse the trie for the padding then for the string. Since the trie has been compressed it will be around 1000 ops in worst case. However it will be even smaller. For seeing which child lies between l and r at each node have a vector which stores all elements that pass through it. Since you will be adding it in order it will be sorted and you can binary search for it.
Just wonderin', can you prove the 1000 part? I have recently faced a problem with the same thing, 1 million characters total in all strings with 1e5 of them. However, the O(N ^ 2) solution passed, with N being the number of nodes in the compressed trie. If you can prove it then that will solve my question for the other one: Is the test — case weak or is O(N ^ 2) supposed to pass
Yeah ok. The worst case for the query will be having as much depth as possible. We do compression to reduce this. So the worst case will occur when the strings are 1,10,100,1000... . However since the total length of input is less than 1e6 the max such strings you will get is around 1000 (Len*(Len+1)/2<=1e6. So Len is around 1000).
How to solve prime trees?
How to solve equations? I know the formulas, but it was difficult for me to use FFT to get better complexity that O(n^2). For example how to calculate those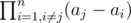 for j = 1, 2, ..., n? Those are the values of P' at a1, a2, ..., an where P(t) = (t - a1)(t - a2), , , (t - an). I can calculate P' in O(nlog2n) using FFT and divide and conquer, but how to evaluate at those points?
for j = 1, 2, ..., n? Those are the values of P' at a1, a2, ..., an where P(t) = (t - a1)(t - a2), , , (t - an). I can calculate P' in O(nlog2n) using FFT and divide and conquer, but how to evaluate at those points?
So a follow up general question: can we having a polynomial of degree n and n points a1, a2, ..., an. Evaluate all P(ai) in parallel faster than O(n2)?
Yes, you can evaluate n points in using FFT. A simple Google search for "multi point evaluation" should give you descriptions. However my implementation was too slow for the time limit.
using FFT. A simple Google search for "multi point evaluation" should give you descriptions. However my implementation was too slow for the time limit.
For reference, my implementation (I can post it later after work) takes ~2 seconds to evaluate a polynomial of degree n = 60'000 at n points (using modular arithmatic). Does anybody have a faster one?
I had the same problem. Precomputing all powers of root for ntt worked for me.
That's a little out of my expectation. My solution takes about 1.2 seconds in total(using multi-point evaluation twice) so I set the time limit to 3 seconds. Maybe your template for multi-point evaluation is too slow.
My code
How to solve Chef and Recipes. I tried Gaussian elimination which passed the small 2 but I could not eliminate excess equations properly leading to TLE or WA.
In short: map 2n to 264 randomly.
Assign a random value (say in [0, 264)) to each base soup and a composed soup's value is the bitwise-xor of the sub-soups' values. For each query use gauss elimination to find if those values are linear independent.
Ok thanks.
I tried doing 60 bits first, but that only passed a couple of files in total, after about half an hour of not finding any other solution, I did 500 bits and it passed
@TLE — Can you explain why this works? When you assign random values to base soups, the xor could collide with an already assigned value right?
The solution seems probabilistic. Since we need at most 30 linearly independent bit vectors per query, it seems the probability that values won't collide is 1 - (30 / 264), which means the overall probability of getting a collision across queries is quite low.
Is there a deterministic solution for the problem under the given constraints?
I have a deterministic solution. My Soln.
Gaussian elimination got accepted (0.2 seconds). However I had to write my own bitset class, since the size of the bitset has to be known at compile time (20'000) otherwise. By writing your own you only need the size to be as big as the number of different base soups. Also you can speed up searching for a pivot element (the first set bit in a bitset) by a factor of 64 pretty easily. My solution
Thanks.
is it bug or not ? other guys have rating that they haved ,but mine is changed .
mgch please response on this.
Probably not a bug. Mine has changed, and a lot of others' has changed too.
i don't know,but only in mine page i see that codechef rating is not similar to codechef rating on graph rating.
UPD:it is fixed now .
Codechef's contest is too hard for me.
Can somebody explain MAGICHF2 with a proper mathematical proof?