Introduction
One of the tasks of last sunday's round problem 755F - Польшар и Подарки was to check if k is the sum of some submultiset of positive integers. The most important observation to solve the problem is:
The sum of all elements in the multiset equals to n ≤ 106.
Wild  solution appeared! But not for me :( In the whole puzzle, this was the only missing part. All I could think was about an O(n2) DP. Although this is a well-known problem with well-known solutions, I couldn't find really good tutorials and I've had to struggle with the poor explanations and the contest's source codes. The most helpful reference was this one, but it does not explain the trick in full details and it only shows half the solution for the problem we'll discuss here. So, in this post, I'll try to explain the solution from the beginning. Of course, any additional good references are welcome in the comments.
solution appeared! But not for me :( In the whole puzzle, this was the only missing part. All I could think was about an O(n2) DP. Although this is a well-known problem with well-known solutions, I couldn't find really good tutorials and I've had to struggle with the poor explanations and the contest's source codes. The most helpful reference was this one, but it does not explain the trick in full details and it only shows half the solution for the problem we'll discuss here. So, in this post, I'll try to explain the solution from the beginning. Of course, any additional good references are welcome in the comments.
I chose a solution that was submitted by at least three different users, including tourist, ershov.stanislav and rajat1603. This is not the easiest solution to understand, but IMHO is the easiest to code. Check my implementation near the end of this post.
Prerequisites
Dynamic programming and bitwise operations.
Problem statement
Warning: Here, n has a different meaning from problem 755F - Польшар и Подарки's n. Symbol k will denote the same thing, though.
You're given a multiset of positive integers X = {(a1, m1), (a2, m2), ..., (an, mn)}, i.e., integer ai occurs mi times in the multiset. Decide if there's a submultiset with sum equals to k. For example, if X = {(1, 7), (3, 2), (19, 5)} and k = 10, then 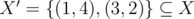 is a solution, because
is a solution, because 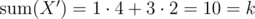 .
.
Let's start with the upper bounds. Without loss of generality, we may assume that:
- The integers ai are such that ai < k, because ai = k yields a trivial answer and ai > k is useless. Therefore we have at most k - 1 distinct integers: n ≤ k - 1 = O(k). And, in the worst case, ai = i.
- The multiplicities mi are such that ai·mi ≤ k, because if ai·mi > k, then we know that the integer ai occurs in the solution at most ci < mi times.
- Remember the n-th harmonic number:
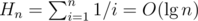 . From that and from the previous bounds, we have
. From that and from the previous bounds, we have 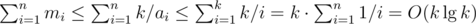 .
. - Finally,
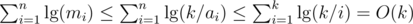 . Proof.
. Proof.
Solutions
Simpler version, naive DP
We could replicate the repeated integers creating a sequence (b1, b2, ..., br) such that 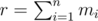 and apply the following dynamic programming.
and apply the following dynamic programming.
Let f(i, j) be  only if it's possible to find a subsequence from (b1, b2, ..., bi) with sum equals to j. Then
only if it's possible to find a subsequence from (b1, b2, ..., bi) with sum equals to j. Then
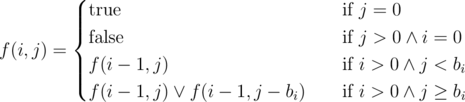
the answer is f(r, k) and the cost is 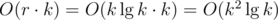 , from Upper Bound 3. The only non-trivial transition is the last: if you can include bi in the solution, you can either take it (subproblem (i - 1, j - bi) remains) or leave it (subproblem (i - 1, j) remains). If any of these choices return
, from Upper Bound 3. The only non-trivial transition is the last: if you can include bi in the solution, you can either take it (subproblem (i - 1, j - bi) remains) or leave it (subproblem (i - 1, j) remains). If any of these choices return  , then subproblem (i, j) has a positive answer.
, then subproblem (i, j) has a positive answer.
Simpler version, tricky DP
The well-known std::bitset data structure is capable of performing O(n) bitwise operations with an O(1 / 32) constant improvement (that actually depends on the underlying integral type being used... std::bitset uses long, which has 32 bits in the Codeforces environment). We can twist the DP above to be suitable for using bitsets.
Let f(i) be a k + 1-length bitset such that j-th bit (0-based) is 1 only if it's possible to find a subsequence from (b1, b2, ..., bi) with sum equals to j. Then
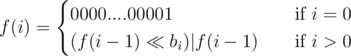
the answer is the k-th bit of f(r) and the cost is 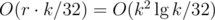 . The non-trivial transition took me some minutes to understand, since I didn't know the precise meaning of this DP. But at this point, I think it's not hard to see that the left shift by bi positions combines all values allowed by subproblem (i - 1) with the current integer bi, while the or ensures that all values allowed by subproblem (i - 1) stay allowed. The latter is the same as leaving the integer bi. Pretty cool, right?! But there's something even cooler!
. The non-trivial transition took me some minutes to understand, since I didn't know the precise meaning of this DP. But at this point, I think it's not hard to see that the left shift by bi positions combines all values allowed by subproblem (i - 1) with the current integer bi, while the or ensures that all values allowed by subproblem (i - 1) stay allowed. The latter is the same as leaving the integer bi. Pretty cool, right?! But there's something even cooler!
Full problem, naive DP
Let's go back to the multiplicities.
Let f(i, j) be  only if it's possible to find a submultiset from {(a1, m1), (a2, m2), ..., (ai, mi)} with sum equals to j. Then
only if it's possible to find a submultiset from {(a1, m1), (a2, m2), ..., (ai, mi)} with sum equals to j. Then
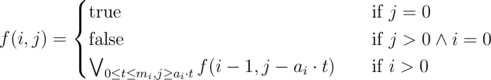
the answer is f(n, k) and the cost is 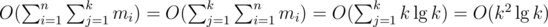 . The only non-trivial transition is the last: all subproblems of the form (i - 1, j - ai·t) are or'd together, subject to 0 ≤ t ≤ mi and j ≥ ai·t. In other words, we consider all possible amounts t of taking ai into the solution. This is pretty much the same DP as the one for the simpler version of the problem. Notice that the upper bounds are the same!
. The only non-trivial transition is the last: all subproblems of the form (i - 1, j - ai·t) are or'd together, subject to 0 ≤ t ≤ mi and j ≥ ai·t. In other words, we consider all possible amounts t of taking ai into the solution. This is pretty much the same DP as the one for the simpler version of the problem. Notice that the upper bounds are the same!
Full problem, tricky DP
Let f(i) be a k + 1-length bitset such that j-th bit (0-based) is 1 only if it's possible to find a submultiset from {(a1, m1), (a2, m2), ..., (ai, mi)} with sum equals to j. Then
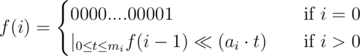
the answer is the k-th bit of f(n) and the cost is 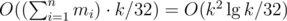 . The non-trivial transition combines all possible amounts t of taking ai into the solution with all the values allowed by subproblem (i - 1). If it's hard to understand this DP, spend some more time in the simpler version. Try to get everything clearly before going ahead.
. The non-trivial transition combines all possible amounts t of taking ai into the solution with all the values allowed by subproblem (i - 1). If it's hard to understand this DP, spend some more time in the simpler version. Try to get everything clearly before going ahead.
Full problem, trickiest DP
Now, we're going to kill that 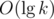 factor. Consider the follwing C++ bottom-up implementation:
factor. Consider the follwing C++ bottom-up implementation:
bitset<MAXK> dp;
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int x = 0; (1<<x) <= m[i]; x++) {
dp |= (dp << (a[i]*(1<<x)));
m[i] -= (1<<x);
}
dp |= (dp << (a[i]*m[i]));
}
// now, dp[k] equals the k-th bit of f(n)
This is the previous DP with a small but very important modification. Instead of blindly or'ing all the possible shifts iterating t from 0 to mi, we do that in a faster and smarter way. We only do that for the first powers of 2 that we can permanently subtract from mi and for the remainder.
The following loop invariant holds in the beginning of each iteration: ai is combined with shifts t = 0, 1, 2, 3, ..., 2x - 1. When x = 0, the invariant trivially holds. Now, suppose this is true for some x. Then combination of shifts t = 0 and t = 2x will produce shift t = 2x. Combination of shifts t = 1 and t = 2x will produce shift t = 2x + 1. Combination of shifts t = 2 and t = 2x will produce shift t = 2x + 2. Combination of shifts t = 3 and t = 2x will produce shift t = 2x + 3... Until combination of shifts t = 2x - 1 and t = 2x produces shift t = 2x + 2x - 1 = 2x + 1 - 1 and the invariant maintenance is complete.
First of all, we just showed that 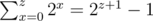 for all non-negative integer z. Now, let y be the value of x after the last iteration. We know that we subtracted
for all non-negative integer z. Now, let y be the value of x after the last iteration. We know that we subtracted 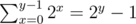 from mi. Then the last bitwise operation for a fixed i combines the shifts t = 0, 1, 2, 3, ..., 2y - 1 with the final shift w = mi - (2y - 1). In the previous paragraph we saw that these combinations yield shifts t = w, w + 1, w + 2, w + 3, ..., w + 2y - 1. The last shift is actually t = mi - (2y - 1) + 2y - 1 = mi. To see that shifts t = 0, 1, 2, 3, ..., w - 1 are also combined, just notice that w - 1 must be less or equal to 2y - 1, since otherwise w would be larger than 2y and the loop would be still running. So we conclude that all shifts from t = 0 to t = mi are now combined in the bitset f(i)! Now, that is cool, right?!?
from mi. Then the last bitwise operation for a fixed i combines the shifts t = 0, 1, 2, 3, ..., 2y - 1 with the final shift w = mi - (2y - 1). In the previous paragraph we saw that these combinations yield shifts t = w, w + 1, w + 2, w + 3, ..., w + 2y - 1. The last shift is actually t = mi - (2y - 1) + 2y - 1 = mi. To see that shifts t = 0, 1, 2, 3, ..., w - 1 are also combined, just notice that w - 1 must be less or equal to 2y - 1, since otherwise w would be larger than 2y and the loop would be still running. So we conclude that all shifts from t = 0 to t = mi are now combined in the bitset f(i)! Now, that is cool, right?!?
The cost of this algorithm is clearly 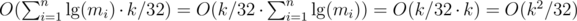 , using Upper Bound 4.
, using Upper Bound 4.
Application to problem 755F - Польшар и Подарки
Warning: The n here refers to problem 755F - Польшар и Подарки's n. It does not refer to the number of distinct integers in the multiset anymore. Symbol k still refers to the goal value, though.
In the more general version of the problem, discussed above, we used the fact that ai·mi ≤ k to state Upper Bound 4: 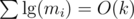 . In the round's problem, we have an even tighter bound. Let me remind you about the first observation of this post:
. In the round's problem, we have an even tighter bound. Let me remind you about the first observation of this post:
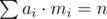
Not only the product ai·mi is bounded by some value for all i, but the whole sum of these products over all i is bounded by that very same value. As proved here, this strong additional constraint gives us the upper bound 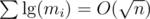 . Hence, the overall complexity using the last algorithm discussed here is
. Hence, the overall complexity using the last algorithm discussed here is 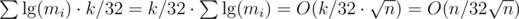 , as k ≤ n.
, as k ≤ n.
Conclusion
Despite these upper bounds and algorithms are well-known to many people, they weren't to me until yesterday. I hope I've gathered all necessary information about this subject in this post and hope this will help others.











This is a nice technique. One thing I'd like to add is that you can put k = min(n - k, k) to gain another factor of two.
Well pointed! But it should be clear that this only works for the round's problem, not the general problem. Thanks for the observation!
No, it's not problem specific. What is problem specific is that we express everything in terms of sum of all numbers, but everything written here is based on assumption that it is small. k is a sum of subset of some numbers if and only if remaining numbers add up to n — k, where n is sum of all of them and that holds in most general (finite :P) setting you can imagine :P.
After applying reductions from Upper Bounds 1 and 2, the sum of all integers will be, in general, bounded by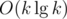 , right? But
, right? But 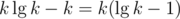 is never better than k...
is never better than k...
Ah, I referred to n as the sum of all integers (as it was when round problem was mentioned), but you also used it later to denote number of different values in multiset, since the confusion I think.
Yeah, sorry for that... I like to use n for the main input size symbol...
UPD: I've included some warnings to avoid this confusion. Thanks for pointing that!
Another problem with similar technique is here : 95E - Счастливая страна.
Thanks for writing the tutorial.
Very nice technique.
In Java we can do the same using BigInteger. I tried with BitSet class as well but it didn't worked well for shifting bits.
Input: ~~~~~ 3 10 1 7 3 2 19 5 ~~~~~
Output: