krismaz's blog

An interesting way to solve 739E
By krismaz, history, 7 years ago, In English

Hi everyone!

I've just solved 739E - Gosha is hunting in an easy but interesting way. However, it's quite different from what's described in the editorial, and I couldn't find any accepted codes that use this approach. That's why I'm curious if anyone solved this problem like me, and if this is a well-known trick :)

First, there's an easy O(n3) DP solution to the problem: for each (i, x, y) compute the best score using x PokeBalls and y UltraBalls on i first Pokemon.

How to improve it? Let's randomly shuffle all Pokemon. If we looked at the first i of them, then we'd expect to use around 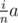PokeBalls, and 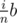UltraBalls there (a and b are the total amount of balls of each type), because the places where we used them in the optimal solution are now randomly distributed... even though positions where we use PokeBalls are not independent from positions where we use UltraBalls.

Now, using some random walk properties we can (I hope!) say, that it's really unlikely that we'll deviate from those expected values by more than . So we can just do the brutal DP, but constrain ourselves to x and y from a specific range of size . After that the solution is O(n2) and get's accepted: 24153740

All opinions are welcome. Thanks :)

  • Vote: I like it
  • +131
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +26 Vote: I do not like it

Is there a way to calculate the chance of failure for a given range — e.g. what's the chance that a range of size O(log(N)) or O(sqrt(N)) (your range) would get WA?

Moreover, is there a way to calculate the optimal strategy (which may involve performing the DP several times over different random arrays and taking the best answer) if we want the confidence to be above a certain number C (C > 0.9995 seems reasonable for a problem with around 100 test cases)?

For example, would it be better to perform the DP four times on a range of sqrt(N)/2 and take the best of the four answers, or perform the DP once on a range of sqrt(N)?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +36 Vote: I do not like it

    You can do something like a Chernoff bound on this. Let σ be permutations. Let Si be the number of Poke-balls in the first i for a given permutation σ.

    So essentially by a Chernoff/Hoeffding bound,

    By a union bound, the total failure probability is  ≤ 2ne - C2 (because there are n values of i and 2 types of balls). So even C ≈ 10 is safe.

    This isn't precise since we're dealing with permutations and not the sum of independent random variables, but its close enough that this should be rigorous.

    So, to answer your question above, consider doubling C. Then your error probability is down to e - 4C2. If you run it 4 times with C, then your error probability is (e - C2)4 = e - 4C2. So its the same!

    → Reply