779A - Pupils Redistribution
Problem setter: MikeMirzayanov
To solve this problem let's use array cnt[]. We need to iterate through first array with academic performances and for current performance x let's increase cnt[x] on one. In the same way we need to iterate through the second array and decrease cnt[x] on one.
If after that at least one element of array cnt[] is odd the answer is - 1 (it means that there are odd number of student with such performance and it is impossible to divide them in two. If all elements are even the answer is the sum of absolute values of array cnt divided by 2. In the end we need to divide the answer on 2 because each change will be counted twice with this way of finding the answer.
779B - Weird Rounding
Problem setter: MikeMirzayanov
To solve this problem we need to make k zeroes in the end of number n. Let's look on the given number as on the string and iterate through it beginning from the end (i.e. from the low order digit). Let cnt equals to the number of digits which we reviewed. If the current digit does not equal to zero we need to increase the answer on one. If cnt became equal to k and we reviewed not all digits we need to print the answer.
In the other case we need to remove from the string all digits except one, which equals to zero (if there are more than one such digit we left only one of them). Such digit always exists because the problem statement guaranteed that the answer exists.
779C - Dishonest Sellers
Problem setters: MikeMirzayanov and fcspartakm
To solve this problem we need at first to sort all items in increasing order of values ai - bi. Then let's iterate through sorted array. If for the current item x we did not buy k items now and if after discounts it will cost not more than now, we need to buy it now and pay ax, in the other case we need to buy item x after discounts and pay bx.
778A - String Game
Problem setter: FireZi
In this problem we have to find the last moment of time, when t has p as a subsequence.
If at some moment of time p is a subsequence of t then at any moment before, p is also its subsequence. That's why the solution is binary search for the number of moves, Nastya makes. For binary search for a moment of time m we need to check, if p is a subsequence of t. We remove a1, a2, ... am and check if p is a subsequence greedily.
778B - Bitwise Formula
Problem setter: burakov28
Note that changing i-th bit of chosen number doesn't change any bits of any of the variables other than i-th one. Also note that the total number of values is greater, as more variables have 1 at i-th position.
Let's solve for every bit independently: learn, what is the value of i-th bit of chosen number. We can try both values and simulate the given program. Choose one of the values that makes more variables to have 1 at i-th position. If both 0 and 1 give equal number of variables to have 1 at i-th position, choose 0.
778C - Peterson Polyglot
Problem setters: niyaznigmatul and YakutovDmitriy
While erasing letters on position p, trie changes like the following: all the edges from one fixed vertex of depth p are merging into one. You can see it on the picture in the sample explanation. After merging of the subtrees we have the only tree — union of subtrees as the result.
Consider the following algorithm. For every vertex v iterate over all the subtrees of v's children except for the children having largest subtree. There is an interesting fact: this algorithm works in 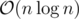 in total.
in total.
Denote as sx the size of the subtree rooted at vertex x. Let hv be the v's child with the largest subtree, i.e. su ≤ shv for every u — children of v. If u is a child of v and u ≠ hv then 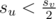 . Let's prove that.
. Let's prove that.
- Let
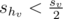 . Then
. Then 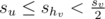 and
and 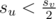 .
. - Otherwise, if
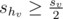 , then we know that su + shv < sv. Therefore,
, then we know that su + shv < sv. Therefore, 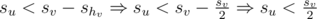 .
.
Consider vertex w and look at the moments of time when we have iterated over it. Let's go up through the ancestors of w. Every time we iterate over w the size of the current subtree becomes twice greater. Therefore we could't iterate over w more than 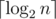 times in total. It proves that time complexity of this algorithm is
times in total. It proves that time complexity of this algorithm is 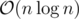 .
.
Solution:
- Iterate over all integers p up to the depth of the trie
- For every vertex v of depth p
- Unite all the subtrees of v with running over all of them except for the largest one.
How to unite subtrees? First method. Find the largest subtree: it has been already built. Try to add another subtree in the following way. Let's run over smaller subtree's vertices and add new vertices into respective places of larger subtree. As the result we will have the union of the subtrees of v's children. All we need from this union is it's size. After that we need to roll it back. Let's remember all the memory cells, which were changed while merging trees, and their old values. After merging we can restore it's old values in reverse order.
Is it possible to implement merging without rolling back? Second method. Let's take all the subtrees except for the largest one and build their union using new memory. After that we should have two subtrees: the largest one and the union of the rest. We can find size of their union without any changes. Everything we need is to run over one of these trees examining another tree for the existence of respective vertices. After this we can reuse the memory we have used for building new tree.
778D - Parquet Re-laying
Problem setter: pashka
Let's assume that the width of the rectangle is even (if not, flip the rectangle). Convert both start and final configurations into the configuration where all tiles lie horizontally. After that, since all the moves are reversible, simply reverse the sequence of moves for the final configuration.

How to obtain a configuration in which all tiles lie horizontally. Let's go from top to bottom, left to right, and put all the tiles in the correct position. If the tile lie vertically, then try to turn it into the correct position. If it cannot be rotated, because the neighboring tile is oriented differently, proceed recursively to it. Thus, you get a "ladder", which can not go further than n tiles down. At the end of the ladder there will be two tiles, oriented the same way. Making operations from the bottom up, we'll put the top tile in a horizontal position.
778E - Selling Numbers
Problem setters: niyaznigmatul and VArtem
Because the target value for this problem is calculated independently for all digits, we'll use the dynamic programming approach. Define dpk, C as the maximum possible cost of digits after we processed k least significant digits in A and C is the set of numbers having the carry in current digit. This information is sufficient to choose the digit in the current position in A and recalculate the C set and DP value for the next digit.
The key observation is that there are only n + 1 possible sets instead of 2n. Consider last k digits of A and Bi. Sort all the length-k suffixes of Bi in descending lexicographical order. Because all these suffixes will be increased by the same value, the property of having the carry is monotone. That means that all possible sets C are the prefixes of length m (0 ≤ m ≤ n) of this sorted list of suffixes. This fact allows us to reduce the number of DP states to O(n·|A|). Sorting all suffixes of Bi can be accomplished using the radix sort, appending the digits to the left and recalculating the order.
The only thing that's left is to make all DP transitions in O(1) time. To do that, maintain the total cost of all digits and the amount of numbers that have the carry. After adding one more number with carry in current digit, these two values can be easily recalculated. After processing all digits in A, we have to handle the remaining digits in Bi (if there are any) and take the best answer. Total running time is 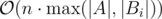 .
.











somebody plzz tell how to do string game using binary search.i read tutorial but i didn't get it..
Let's consider the first test case, where you have this order of deleting characters:
Let's write down if we could obtain the target word after deleting characters order[0], order[1], ... order[i] of the original word (Note that we always delete characters in this order):
This sequence is monotonous and thus, we could do a binary search to find the maximum index, which brings "YES". :)
Hope that helps!
Help me plzzz,What's wrong with my code ? (time limit on test 10) String game 25102212
It's a bruteforce, not a binary search.
Where's the editorial for Div. 1 C and Div. 1 D?
The way I implemented C was pretty much brute force, but if you calculate the complexity it's N * 26 Log(N).
For each node U, you count how many duplicate nodes you'll have in its subtree if you remove it and its outgoing edges. We add this to the number of removals for level(U) + 1.
So you'll have a dfs(vector v), where all vertices in v are equivalent with respect to U (same prefix in the sub-trie). Since all are equivalent you add v.size()-1 to the number of duplicates. Now for every letter c, you make the vector of nodes that are children of a node in v through an edge labelled with letter c. Now do (at most) 26 dfs calls, one for each new vector. If the current size of the node vector is 1 or 0, you stop since there won't be any extra duplicates. The initial call is dfs(children of U).
Submission
Your solution is also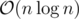 , because if the size of v is 26, then n is distributed in this 26 subtrees, so every time you call
, because if the size of v is 26, then n is distributed in this 26 subtrees, so every time you call
dfs3withv.size() == k, you use k nodes. You use only nodes, which are duplicate, that's why it's the same as if you only iterated over the small subtree.Can you elaborate on the the statement: "The complexity is N*26log(N)". That is the most vague part in your solution
778C: I dont know why you wrote about biggest child of vertex. I implemented your solution and then removed "lets merge all subtrees to the biggest subtree" rule — it became even faster (935ms 146Mb vs 732ms 124Mb)
So plain solution with rollbacks works.
No, your solution makes link to whole subtree, instead of copying it. That's why your merge function works in min(s1, s2) time, where s1 and s2 are the sizes of the subtrees, which is equivalent to iterating over "all vertices in all subtrees except the largest one".
Could you please explain why they are equivalent? It really puzzled me.
Because
dfsvisits vertex for the first time if it's in both subtrees, that are being merged. Every next time the vertex is visited, it appears again in a new subtree. It means vertex is visited k - 1 times, if it appeared in k subtrees. So, consider biggest subtree and for every vertex this - 1 from k - 1 means "we don't visit biggest subtree".Got it. Thanks a lot.
what is wrong with my appraoch for "778C — Peterson Polyglot"? normal dfs when i enter vertex i try to kill its children and count the children of the children which occur more than once + number of its children and update kill[depth] after that iterate over kill get the largest one x to be the solution (n-x)... can any one help me http://codeforces.com/contest/778/submission/25119082
I got the same problem. Try this test case 7 1 2 a 1 3 b 2 4 b 4 6 c 3 5 b 5 7 c
This should've been in pretests before the big test case # 3.
Can someone explain the time complexity of the binary search solution to the String Game problem?
I hope someone reply, especially the author Mr.niyaznigmatul :).
In problem 779C, what's about this approach?:
We firstly iterate over the
nnumbers and take all items which its cost now is less than or equal to its cost after week, because we need to buy at leastkitems now. So, we can buy more thankitems!Secondly, for the rest of the items, we do what the approach in the editorial do.
This is my submission which depends on my approach and gets WA.
Please, reply.
UPD: I was wrong when I think that my approach is deferent from the approach mentioned in the editorial. I used
setdata structure for sorting, ignoring that there may be equal entries. Now I fixed my code :). Sorry for disturbing you.Can u please help me in string game problem.
I am not getting how to apply binary search.
Please tell the approach and if possible please share your code with comments, that would me to understand in better way