Пусть у нас есть связный неориентированный граф без петель и кратных ребер, в котором n вершин и m ребер. Докажите, что в нем найдется C·n2 / m вершин, которые попарно не соединены ребрами, где C — какая-то абсолютная константа.
→ Обратите внимание
До соревнования
EPIC Institute of Technology Round Summer 2024 (Div. 1 + Div. 2)
35:29:16
Зарегистрироваться »
EPIC Institute of Technology Round Summer 2024 (Div. 1 + Div. 2)
35:29:16
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3845 |
| 2 | jiangly | 3707 |
| 3 | Benq | 3630 |
| 4 | orzdevinwang | 3573 |
| 5 | Geothermal | 3569 |
| 5 | cnnfls_csy | 3569 |
| 7 | jqdai0815 | 3532 |
| 8 | ecnerwala | 3501 |
| 9 | gyh20 | 3447 |
| 10 | Rebelz | 3409 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | maomao90 | 171 |
| 2 | awoo | 163 |
| 3 | adamant | 162 |
| 4 | maroonrk | 152 |
| 5 | nor | 151 |
| 5 | -is-this-fft- | 151 |
| 7 | atcoder_official | 147 |
| 7 | TheScrasse | 147 |
| 9 | Petr | 145 |
| 10 | pajenegod | 144 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 29.06.2024 06:05:45 (f1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Я правильно понимаю, что задача эквивалентна следующей: найдите минимально возможный размер клики в графе с n вершинами и n2 - m рёбрами?
Да, независимые множества и клики дополняют друг друга.
Рассмотрим произвольную вершину. Если степень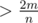 , убьём её; n2 / m изменится на что то, большее (n - 1)2 / (m - 2m / n) = (n2(1 - 2 / n + 1 / n2) / (m(1 - 2 / n)) ≥ n2 / m. Продолжим решать задачу для полученного графа.
, убьём её; n2 / m изменится на что то, большее (n - 1)2 / (m - 2m / n) = (n2(1 - 2 / n + 1 / n2) / (m(1 - 2 / n)) ≥ n2 / m. Продолжим решать задачу для полученного графа.
Теперь пусть степень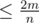 . Тогда выкинем эту вершину и все с ней смежные, решим задачу для оставшегося, добавим к ответу вершину. Чему же будет равно отношение n2 / m для оставшегося графа? Понятно, что оно не меньше (n - 2m / n)2 / m = n2 / m - 4 + 4m / n2. Т.е. мы уменьшили отношение на 4 ценой увеличения ответа на 1, значит, этот алгоритм решает задачу с C = 1 / 4.
. Тогда выкинем эту вершину и все с ней смежные, решим задачу для оставшегося, добавим к ответу вершину. Чему же будет равно отношение n2 / m для оставшегося графа? Понятно, что оно не меньше (n - 2m / n)2 / m = n2 / m - 4 + 4m / n2. Т.е. мы уменьшили отношение на 4 ценой увеличения ответа на 1, значит, этот алгоритм решает задачу с C = 1 / 4.
а откуда задача?
Мне ее дали в качестве домашнего задания, я не смог справиться и вот теперь спрашиваю уважаемое сообщество.
А если серьезно, то сложно сказать, откуда она изначально. На ней удобно демонстрировать вероятностный метод. Вот что имеется ввиду.
Пусть мы хотим выбирать наше независимое множество случайно. Будем включать каждую вершину в него независимо с вероятностью p. Тогда в среднем останется pn вершин и p2m ребер. Но давайте теперь у каждого оставшегося ребра выкинем по концу. Тогда в среднем останется независимое множество размера pn - p2m. Теперь, выбирая p оптимально, получаем требуемую оценку с C = 1 / 4.
Похожей техникой можно доказать, что если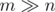 , то, как бы мы не укладывали граф на плоскость, получится не менее C·m3 / n2 пересечений ребер. Подробнее см. здесь.
, то, как бы мы не укладывали граф на плоскость, получится не менее C·m3 / n2 пересечений ребер. Подробнее см. здесь.
А почему в минусах? Может парню интересно, где еще найти таких задач
Люди такие непредсказуемые...
ошибся