Tutorial is loading...
Tutorial is loading...
Simple implementation of solution described higher: http://ideone.com/IoSts1
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
Simple implementation of solution described higher: http://ideone.com/IoSts1
| Name |
|---|



Auto comment: topic has been updated by wrg0ababd (previous revision, new revision, compare).
I think Problem D constraints are very bad, because O((n + m) * n ^ 2 * k) solutions passed, but there is O((n + m) * n * k) solution...
What is the difference between intervals and segments?
I think segment contains it's borders, interval doesn't
segments are empty if l > r
but intervals are empty if l >= r
For Problem C, making the value of eps more precise changes verdict from WA to AC. But, aren't we supposed to take any difference < 1e-6 as zero, as it is mentioned in the problem statement as well, that even the judge will compare the answers with error limit = 1e-6?
It's not fair, i think, but in statement it says that it compares answers, but not anything else, printing -1 should be very precise :/
The problem is there was a case (40) where using a large epsilon would give -1 but the answer was actually 0.99998999989999903804, so the output is completely off from the answer.
I thought that there has to be an equal number of vertices instead of leaves in E. The renaming of "leaves" and "vertices not being leaves" to "offices" and "departments" was strange. ;_;
Problems were confusing to be honest, I fell for it too.
Same! I get that they try to wrap the problem in something so that it doesn't seem boring, but clarity should be the #1 priority always.
It's a shame as well, I really liked the problem otherwise.
I tried the following for problem C:
But I got WA on test 30 because of the precision error. Can you find where I did the mistake? and How to find a good EPS which will meet the requirement.
Submission: http://codeforces.com/contest/793/submission/26625111
here is my Solution for B i used almost exactly what you mentioned first (naive recursive). passed pretests but got TLE on test 10.
adding the below code passes test 10 but TLE on 11. any help please?
if(turns==2 && (dir=='u' || dir=='d') && y!=sj) return;
if(turns==2 && (dir=='l' || dir=='r') && x!=si) return;
26615391 : same solution. TLE on test 10.
My problem was TLE, and it's solved by using a boolean visiting 4D array to mark the position I have already checked with the direction and number of turns that I have checked the position with.
Your solution is 90% identical to mine what a coincidence :D however i didnt use the visited array and still it worked in less time even thought im using java, i dont think u need the visited array maybe u have to recheck ur base case conditions or the recursive function , or maybe stop it when u have done already 2 turns and ure not the same line or column of the destination, cause in that case ull need one more turn to get to dest, so stop it from the beginning when turns=2 and Tx!=x and Ty!=Y
Here is my code 26655398. I have already put these return cases you mentioned. However, I'll back to this problem soon, thank you:D. Edit: please look back to my previous comment, direction instead of destination, sorry for this mistake.
It seems to me C is in something easier to solve this way(sorry if someone have alredy written about this): We used bisection method for minimal time calculate. Let start with
L=0, R=10^11. Let us now be at timeM = (L + R) / 2. Then it is easy to calculate for every mouse her coordinatesXiandYi. Obviously whenYi >= Y2 and her y-speed >= 0, we must move the right border, since she will never be inside a rectangle. Similarly examine the three other cases:Yi <= Y1 and y-speed <= 0Xi <= X1 and x-speed <= 0Xi >= X2 and x-speed >= 0And we must move the right border, if all mouses are in the rectangle. If these conditions are not met, move the left border. When we have done all iterations, we have right border as an answer. We will get it, if all mouses were in the rectangle at the same time. Else deduce
-1B has easier solution. Paint crosses on S and T with different colors (say 's' and 't'), then examine each line and each column if any of them contains
/S\.*T/ or /T\.*S/(c++26615732).Awesome idea! Thank for your share!
Similar idea:
1. Paint 's' to the left and to the right from 'S'. Same with 'T'.
2. Rotate whole field.
3. Repeat step "1".
4. Try to find
S+dots+TorT+dots+S(ignoring case).5. Repeat step "2".
6. Repeat step "4".
Implementation in perl (26638162).
Why do you give him so many downvotes?After all he prepared the round and posted the editorial!
The post is hidden because of too negative feedback, click here to view it
Same code shows two different verdict why?
Accepted code: Wrong Answer code:
The code works fine with C++14 but not with C++11 but I don't know why, maybe it's a precision-related issue.
Hmm ,THis is problem with Language c++11 and c++14
For problem B, I got WA on test 62. Here is my submission: 26615111
Can anybody help me ? What's wrong in my code ?
Update: I have found my bug. I was using visited array as vis[row][col][mov], using visvis[row][col][dir][mov] got AC. Here is my AC code: 26632674
I have written dfs solution for Problem B but it has got WA for test case 24.
you can visit cell before but with more turns, you need to add number of turns in used. 26637049.
thank you so much :)
I don't like this round...
In problem B, I used DP to get the minimum number of direction changes to reach 'T' from a given cell.
The DP state is: (row, column, current direction).
If the starting cell can reach 'T' in 2 direction changes or less, then the answer is YES.
This code gives me WA.
Is there a logical problem with my method?
You essentially do a DFS instead of a BFS, so when you find a path, it is not necessarily the shortest one.
In other words, such a dynamic programming solution should care about the order of visiting the cells, and yours doesn't.
How can problem B be solved just using 3(currx,curry,dir) states in case of bfs whereas for recursive dfs I need 4 states (currx,curry,dir,turn). I couldn't understand this part can someone explain it to me . Thank you
Using 0 - 1bfs, a bfs on a graph where the edges weights are 0 or 1. This BFS instead of using a queue, uses a deque (double ended queue).
If you change the direction, then this edge has weight 1, otherwise it has weight 0. If you go through an edge with weight 1, push it to the end of the deque, otherwise push it to the front.
While doing the BFS, always pop the front of the deque
For Problem G,could anyone please tell me the detailed way to cut the field into O(n) rectangles without deleted cells? I can't understand the way mentioned in the editorial.Thanks!
In my solution, I did a scan line, maintaining a partition of (currently) non-deleted rows into ranges in a map. There will be two types of events:
The algorithm will create non-deleted rectangles for ranges 2, 3 and 4 and create two new ranges as shown above.
My solution for reference (submit).
Thanks a lot!
Can E be solved for N ≤ 106? It's possible to calculate knapsack for this constrains.
Yes, should be doable in O(n*(sqrt(n)+log^2(n))) with FFT convolutions.
How ?
Here is the simpler version in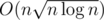 and small constant (/64 with bit-compression): Let's split the weights into two groups:
and small constant (/64 with bit-compression): Let's split the weights into two groups: 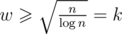 and w < k.
and w < k.
In the first group, there are at most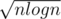 values (because their sum doesn't exceed n).
values (because their sum doesn't exceed n).
In the second group, there are at most k distinct values, and each group of equal weight w can be replaced with O(logn) equivalent (for knapsack) weights: if there are m weights equal to w, let's replace them with w, 2w, 4w, ...,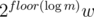 ,
, 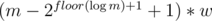 .
.
This way, we can reduce the size problem to at most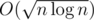 weights, which can be solved with regular knapsack dp (possibly with bit-compression)
weights, which can be solved with regular knapsack dp (possibly with bit-compression)
Let's replace different weights by the same bound.
different weights by the same bound.
w,w,wby2w,wwhile we can (it my be done in O(n)), after that it will be onlySo extra log is not needed
Nice trick, thank you!
Can someone give more detailed explanation of problem D ?
Thanks
Ok, I'll try explain my solution
Oleg can't go near offices he visited, so if now he is in office v, he visited q, q > v, he can't visit office k, where k > q. That means if now he's in office v, he can only visit office q, l < v < r, l is rightmost visited office which position is less than v and r is leftmost visited office which position is more than v. So we have to solve our problem for state [v][l][r][s], where s count of steps we made. We have 2 options. First is go to left and second is go to right. If we go left, we are not interested what is r, and if we go right we are not interested what is l. So our state now is [left border][right border][direction][s]. State [v][l][r][s] becomes 2: [v][r][right][s] and [l][v][left][s]. We can exactly identify our current position. If we go left it's right border, and if we go right it's left border. Now, when we are in state [l][r][direction][s] and now we are in office v, we have to just find all offices q, l<=q<=r and c[v][q] != 0 and solve our problem for [l][q][right][s+1] and [q][r][left][s+1] and take minimum. For it we can use recursion. We can start from any office, so we have to solve problem for [0][v][left][0] and [v][n+1][right][0] and take minimum.
We have n^2*2*k states. In each state we check make not more than n operations. So algo works in O(n^3*k)
How is the time complexity O((n+m)*n*k). I didn't even understand how the naive algorithm works in O((n+m)*n^2*k)
Problem G can be solved using Hopcroft-Karp algorithm, if you optimize it hard enough: 26669894.
I think problem B has a better solution with brute force and a little dp firstly, initialize 2 arrays h and v so that h[i,j]=number of cell with road work from (i,1) -> (i,j) and v[i,j]=number of cell with road work from (1,j)->(i,j) since igor can only make 2 turns so his way must be one of these: --- — ---- | ^ | | | | | | <-- --> | V ---- so we just need brute force and calculate the number of cell with road work on the path (get it from h and v cause he can only go up, down, left or right)
Problem F has a tag "divide and conquer". Is there a solution with O((n + m + q)polylog(n + m + q)) time complexity?
Yes. Check submission of niyaznigmatul: 26621779.
Thanks!
For other people who are trying to understand this code: The setmin function sets every element of the interval to be the minimum of its value and val. The getmin function returns the first index in the interval whose value is larger than val.
I have a solution for problem F with time complexity O((N+M)logN) using segment tree.
Would you be nice to explain your solution? thanks in advance
Would you be nice to explain your solution? thanks in advance
Just in case someone is looking for a proof for problem A (793A - Oleg and shares)
We can't increase the values of any number, so we have to make bigger numbers equal to smaller numbers by subtracting k (zero or more times) of them.
Suppose the array is sorted.
At some point we'll have to make numbers arr[i] and arr[0] equal, and the only way is by subtracting k from arr[i] some number (q) of times and subtracting k from arr[0] some number (p) of times so we have: (a = arr[0], b = arr[i] for simplicity, 0 < i < n)
a — pk = b — qk
(b — a) = k (q — p)
We don't know (and we don't need to know) values p and q, but now it's certain that (b — a) must be divisible by k.
Now the key step is that if k divides (b — a), then we can make b equal to a by subtracting k (b — a) / k times because the only criteria to make a = b — qk is that k divides (b — a). This is optimal.
Getting W.A. for problem B......Can anyone provide a test case for which this fails?
Very easy solution brute force solution B- no DP or dfs/bfs at all. It takes full advantage of the fact that the solution must use at most 2 turns:
Because of the two turns limitation, there are two possible cases for our final path. Our directions for the travel can either be
D/U => L/R => D/UorL/R => D/U => L/R.Assuming the two locations are
(r1, c1), (r2, c2), the first case case can be handled as such:Iterate through all subarrays
board[i][c1:c2]. If a subarray with 0 obstacles inside is found, and the subcolumnsboard[i:r1][c1]andboard[i:r2][c2]also contain 0 obstacles, then we've found an answer. These subarrays/subcols by themselves will represent a valid 2 turn path, so if they contain no obstacles, it is obvious an answer has been found.This same logic can also be applied to the second case. If searching both cases yields no answer, then we can safely return "NO".
Accepted implementation: https://codeforces.com/contest/793/submission/164203477