kpw29's blog

Baltic Olympiad In Informatics 2017
By kpw29, history, 7 years ago, In English

Hi everyone!

Baltic Olympiad in Informatics is being held in Bergen, Norway. Here is the official competition site.

I am wondering — will there be any online mirror? It would be great if there actually was one, it doesn't seem probable :/

  • Vote: I like it
  • +32
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +14 Vote: I do not like it

Seems like you can register in https://boi17-open.kattis.com/ provided in the official website.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +15 Vote: I do not like it

    How do you find the list of Kattis mirrors like these? For example, naipc17.kattis.com, etc? I've searched kattis but there's no list of these subdomains.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      sorry but i found the website in the official boi webisite > <. But I think searching site:kattis.com naipc17 or boi17 or other contest in google can find the result

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      BOI is held on Kattis this year, that's why there even is a Kattis mirror.

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Also, the public ranking of an onsite contest will be available here: https://boi17-public.kattis.com/

    → Reply
»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Can please someone share solutions?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Problem 3

    Spoiler
    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 3   Vote: I like it +5 Vote: I do not like it

      Can you please share more details? I don't understand your idea.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 7   Vote: I like it +3 Vote: I do not like it
        Spoiler

        I know my English and presentation is just awful. You can take a look of my code http://ideone.com/fFIXFT

        → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +19 Vote: I do not like it
      Simpler solution
      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I feel very troll now :'(

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I guess you add 1 using prefix sums?

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +4 Vote: I do not like it

          w prefix sum + lca

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            But how does this work on the right side? In DFS order to the left you have straight chains so you can do prefix sums. But when you go right, there are paths to the left between "straight chains", so more connections are counted (as necessary).

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it +3 Vote: I do not like it

              Yes. And in fact, it is counted exactly twice. So there's no difference.

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                7 years ago, # ^ |
                  Vote: I like it 0 Vote: I do not like it

                When you must output the edges, how do you know which are counted due to right prefix sum?

                → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                    Vote: I like it +3 Vote: I do not like it

                  Ah now I realize your point. That's why I separate path s — e to s — lca(s, e) — e. This separation yields two path to root, which you called as "straight chains".

                  → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                  ← Rev. 2   Vote: I like it 0 Vote: I do not like it

                  I don't understand something. Let's say s is in left subtree of LCA(s, e) and e is in right subtree of LCA(s, e). Adding s is not problem. But I can't find an efficient way to add only chain to the right. Can you share your code, please. Maybe this will help.

                  → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                    Vote: I like it 0 Vote: I do not like it

                  Now I don't realize what you are curious for... whatever, this is my AC code, as you requested.

                  https://github.com/koosaga/olympiad/blob/master/Baltic/baltic17_railway.cpp

                  → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                    Vote: I like it 0 Vote: I do not like it

                  Thank you very much. I understand now. I thought you did cnt[i] += cnt[i — 1] according to DFS traversal array, not another DFS. That clarifies everything.

                  → Reply
»
7 years ago, # |
  Vote: I like it +4 Vote: I do not like it

How to solve A ???

:)

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it
    Spoiler
    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      How do you find cliques containing that node in O(2^k)?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        We know there must exists a node X with at most K neighbors. We'll find the one with minimum number of neighbors (so, at most K). Now, if we want a clique containing the node X, its members are limited to X and X's neighbors. Now, you can choose the subset of neighbors of X that are contained in the clique and check if they really form a clique. In my source, I've reindexed the nodes with numbers from 1 to K + 1 and remembered for each pair whether there is an edge or not. To do it, I just used a set, but it generally work with any hash (hence, K^2logM or K^2 time complexity for each iteration, but it's negligible compared to 2^K)

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Thanks a lot. Could you please briefly tell the solution to the second task?

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            First, divide nodes of the original graph into N/K groups so that node number I belongs to the group I/N. Now we can define a single node X by its group number X/K and X mod K. As a preprocessing we store T[g][m1][m2][i] which denotes minimum distance from node which belongs to group g, is m1 modulo K to node in group g + 2^i, which is m2 modulo K. We can calculate this table by simple for loops. When we receive a query we can simply change nodes a,b to their groups g1, g2 and rests m1, m2, and then iterate through all bits of number g2 — g1 (jump pointers) in order to perform a simple "dp", we simply move number g1 to the right by powers of 2 contained by number g2-g1 and calculate our partial result (res[x] table which denotes distance from node a to current jump with modulo K equal to x) based on previous "jumps". After the iteration we print res[m2]. Time and memory complexity is something like N*K^2*logN.

            → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Correct me if I'm wrong, but I understood, that it's sufficient to apply such algorithm: 1) Select a vertex with min degree, remove it from the graph, reduce all its neighbours degree by 1 and put them in priority queue 2) Try all subsets of its neighbours to form maximal clique (as you've mentioned, the complexity of such process is 2^K, where K doesn't exceed 10? (or what?)(why does it always hold, as total neighbours count can be N-1?) And what's the overall complexity of yours solution? Is it N * 2^K?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        You understood it right.

        Total neighbor count can be N-1, but you selected a vertex with min degree, and there always exists some vertex with deg <= K (Because, by statements, such vertex always exists in any subgraph), So trying all subsets are sufficient.

        My complexity is N * 2^k * k^2

        → Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

Will there be an online mirror for the second day?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

No, really, will there be an online mirror for day 2? Cause' it's about to start.

→ Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Is there a solution easier (to write) than centroid decomposition with a segment tree for 6th problem?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    Apparently this problem is a weaker version of this Atcoder problem.

    → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +16 Vote: I do not like it

    yes it is. I wrote just simple linear dp and it passes.

    in each node I remember two values:

    • the distance to the nearest cat already marked

    • the distance to the farthest node on which we can still put a cat

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +16 Vote: I do not like it

      Can you elaborate a bit? I've had an idea of another DP, but a much more complicated one. Your idea seems too simple.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        here is a (not so neat) code: https://pastebin.com/XuCnE25D

        The idea : we replace each subtree by a path of len <= d/2 such that the answer will not change.

        Suppose that our current node is v and we want to replace its subtree by a path. And we already replaced childs subtrees by some paths. If all those paths are shorter than  < d / 2 then we leave only the longest path.

        If there are paths of length d / 2 then we put a cat at the bottom of such paths and delete this part from the tree. (be careful when d is odd).

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +18 Vote: I do not like it

          6 5 0 1 2 3 0

          Your program outputs 1, answer is 2.

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it +5 Vote: I do not like it

            yep. Still it gets 100 at kattis.

            I guess the issue is with the condition at the end when we finally reach the root we sometimes should add 1 to the answer...

            → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +24 Vote: I do not like it

    Tests for p6 seems pretty weak (my n^2 testing code unexpectedly got AC)

    → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it +21 Vote: I do not like it
    Spoiler

    Code

    However I think there are simpler solution than this.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it -10 Vote: I do not like it

      Can you give a proof that picking farthest node is optimal?

      → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it +16 Vote: I do not like it

      2 years later, and I still don't know why picking the furthest node is optimal :((

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can please someone share solutions of second day?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +7 Vote: I do not like it

    for B just observe that there are two types of possible boards:

    A[i, j] = ( - 1)xi + j for some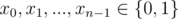

    A[i, j] = ( - 1)i + yj for some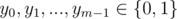

    and each constraint gives us the values of xi, yj

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      So answer is only 0, 1, 2? Or do I have to do some kind of DP?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Let us look at the possible boards of the first type. There are two possibilities:

        • constraints are inconsistent for example one gives x1 = 1 and the other x1 = 0. in that case there are no solutions.

        • there are k different constaints. In that case there are 2n - k possibilities.

        Do the same for the second type. And be careful because there are two colorings (usual chessboard) which are of the both types.

        → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 4   Vote: I like it +82 Vote: I do not like it

    A: Solution sketch (I didn't implement the solution, though):

    1. Check if the relation of friendship is symmetric.
    2. Prove that there is solution in which each group is connected (if it's not, break each group into its connected components).
    3. Let cluster be a group whose size (call it p') not larger than p and having no more than q outgoing edges (let this number be q'). We allow clusters to be empty (it really changes nothing). For each vertex v, backtrack to find all connected clusters containing v. In each recursive step, take a vertex adjacent to our current group and decide (recursively) whether to take it to the set or say it's not going to be in the group. The first decision increases p', the second increases q'. Each recursive step increases p' + q', which in turn cannot exceed p + q. Total complexity of one backtrack is O(2p + q) (something like that). On each turn, we can check if our current set is a cluster (and, as we'll see later, we can actually terminate the backtracking when we find any such cluster). As we run it for each vertex, total running time is O(n2p + q). And probably much faster.
    4. If there's no cluster containing some vertex, the answer is NO.
    5. In the opposite case, for each vertex pick any cluster containing it. It gives us n clusters covering all the vertices. Now for each pair of selected clusters A, B we're going to transform them (to A', B') so that and . We can prove that at least one of , is a cluster (some easy inequalities on the number of the outgoing edges). If the first one is a cluster, transform (A, B) into . The second case is symmetric.
    6. After running the reduction on pairs of clusters above, we're left with a set of clusters (some of them might be empty) which are pairwise disjoint and cover all the vertices. This completes the construction. The complexity of this phase is O(pn2).
    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +40 Vote: I do not like it

I'm sorry to revive the topic. Although the contest is over, but does someone know whether it will be possible to submit solutions for Day 1 contest? Because it appears, that only submitting problems for Day 2 is available at the moment, or am I missing something?

→ Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it +13 Vote: I do not like it

Is there any way to submit solutions now? The Kattis contest is dead.

UPD: Apparently not...

→ Reply