abbi_18's blog

Stuck at finding number of rotations.
By abbi_18, history, 7 years ago, In English

I recently saw a question and was stuck on it for quite some time. Let's say if there are 'n' people standing is a circle. Now I will talk to the 1st person, then skip next 'a' people and talk to (a+2)-th person. I am supposed to calculate the number of people I have to talk to, before I can talk to the 1st person again.

Eg 1: The number of people = 10. The number of people to skip = 3.

so, the order in which I will go to people is -> 1 5 9 3 7 1 here, we can see that I had to go through 4 people to reach to 1 again.

Eg 2: The number of people = 10. The number of people to skip = 1

the order to reach out to people -> 1 3 5 7 9 1 here, 4 people were visited before reaching to 1 again.

Now the naive approach to solving this problem will be to iterate over the array but that will give me a time complexity of O(n) but if the number of people standing in the circle is of the order 10^18. This will not work.I think a better way to approach this problem would be by the help of gcd operation but I am not able to figure out the correct specifics of that approach. Also, Is there a approach to solve these type of questions.

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Constraints on a? If it is less than 107, then there is an O(N) solution that would be fast enough.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks for commenting, Rishi. Although that would be correct; I am looking for a solution which will be work in O(1) or at least in O (log n).

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Isn't the first sequence wrong? 1, 5, 9, the next number should be 3. Coz we skip 10, 1 and 2.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Yes, It should be. I corrected it now. Thanks

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +6 Vote: I do not like it

          If what I understood is correct, the answer to the problem is

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it +6 Vote: I do not like it

            Here is the proof:

            We need to visit 1 again. Let us suppose we visit it after going over the array [1, n], t times. To make it clear, t means how many times you skip the nth person.

            So you need to solve this equation for x(can be obtained by analysing a simple AP):

            t × n + 1 = 1 + (x - 1) × (a + 1).

            Therefore .

            For this to be an integer, t should be .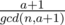

            Here x will give us the xth term of A.P., so we need to subtract 2 because you want to find out how many terms you skip.

            So substituting t and subtracting 2, we get

            .

            You might need to handle some corner cases, haven't given much thought.

            → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
            ← Rev. 2   Vote: I like it 0 Vote: I do not like it

            Yes, This will work. I was just looking around gcd but was not able to figure out this particular expression. Thanks for the help :)

            → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by abbi_18 (previous revision, new revision, compare).

→ Reply