Tutorial is loading...
First accepted Div1: 00:00:58 kriii
First accepted Div2: 00:00:59 Baneling3
Author's solution
int a, b;
scanf ( "%d%d", &a, &b );
int ans = 1;
for ( int j = 1; j <= min( a, b ); j++ )
ans *= j;
printf ( "%d\n", ans );
Tutorial is loading...
First accepted Div1: 00:03:30 Egor.Lifar
First accepted Div2: 00:04:43 Baneling3
Author's solution
const int maxn = 1050;
vector < int > ans;
vector < int > newAns;
char t1[maxn];
char t2[maxn];
int n, m;
scanf ( "%d%d\n", &n, &m );
gets( t1 );
gets( t2 );
for ( int j = 0; j < n; j++ )
ans.pb( j );
for ( int j = 0; j < m - n + 1; j++ ) {
newAns.clear();
for ( int i = 0; i < n; i++ )
if ( t1[i] != t2[i + j] )
newAns.pb( i );
if ( newAns.size() < ans.size() )
ans = newAns;
}
int sz = ans.size();
printf( "%d\n", sz );
for ( int j = 0; j < sz; j++ )
printf( "%d ", ans[j] + 1 );
Tutorial is loading...
First accepted Div1: 00:08:30 nuip
First accepted Div2: 00:10:19 ColdSu
Author's solution
const int maxn = 200500;
const int inf = ( 2e9 ) + 2;
vector < pair < pair < int, int >, pair < int, int > > > queries;
int bestCost[maxn];
int l[maxn];
int r[maxn];
int cost[maxn];
int solution( int n, int needLen ) {
queries.clear();
for ( int j = 0; j < n; j++ ) {
queries.pb( mp( mp( l[j], -1 ), mp( r[j], cost[j] ) ) );
queries.pb( mp( mp( r[j], 1 ), mp( l[j], cost[j] ) ) );
}
for ( int j = 0; j < maxn; j++ )
bestCost[j] = inf;
ll ans = 2LL * inf;
sort( queries.begin(), queries.end() );
int sz = queries.size();
for ( int j = 0; j < sz; j++ ) {
int type = queries[j].f.s;
if ( type == -1 ) {
int curLen = queries[j].s.f - queries[j].f.f + 1;
if ( curLen <= needLen )
ans = min( ans, 1LL * queries[j].s.s + 1LL * bestCost[needLen - curLen] );
}
if ( type == 1 ) {
int curLen = queries[j].f.f - queries[j].s.f + 1;
bestCost[curLen] = min( bestCost[curLen], queries[j].s.s );
}
}
return ans >= inf ? -1 : ans;
}
Tutorial is loading...
First accepted Div1: 00:15:47 arsijo
First accepted Div2: 00:18:01 ColdSu
Author's solution
const int maxn = 5000500;
int isPrime[maxn];
ll dp[maxn];
int main()
{
int t, l, r;
scanf ( "%d%d%d", &t, &l, &r );
for ( int j = 2; j < maxn; j++ )
isPrime[j] = j;
for ( int j = 2; j * j < maxn; j++ )
if ( isPrime[j] == j )
for ( int i = j * j; i < maxn; i += j )
isPrime[i] = min( j, isPrime[i] );
dp[1] = 0;
for ( int j = 2; j < maxn; j++ ) {
dp[j] = 1LL * inf * inf;
for ( int x = j; x != 1; x /= isPrime[x] )
dp[j] = min( dp[j], 1LL * dp[j / isPrime[x]] + 1LL * j * ( isPrime[x] - 1 ) / 2LL );
}
int ans = 0;
int cnt = 1;
for ( int j = l; j <= r; j++ ) {
dp[j] %= base;
ans = ( 1LL * ans + 1LL * cnt * dp[j] ) % base;
cnt = ( 1LL * cnt * t ) % base;
}
printf ( "%d\n", ans );
}
Tutorial is loading...
First accepted Div1: 00:43:18 Pepe.Chess
First accepted Div2: 01:05:21 CountOlaf
Author's solution
import java.io.*;
import java.util.*;
public class Main implements Runnable {
static class InputReader {
BufferedReader reader;
StringTokenizer tokenizer;
InputReader(InputStream in) {
reader = new BufferedReader(new InputStreamReader(in), 1 << 20);
tokenizer = null;
}
String next() {
while (tokenizer == null || !tokenizer.hasMoreTokens()) {
try {
tokenizer = new StringTokenizer(reader.readLine());
} catch (IOException e) {
e.printStackTrace();
throw new RuntimeException(e);
}
}
return tokenizer.nextToken();
}
int nextInt() {
return Integer.parseInt(next());
}
long nextLong() {
return Long.parseLong(next());
}
double nextDouble() {
return Double.parseDouble(next());
}
}
static long[] unique(long[] arr) {
Arrays.sort(arr);
int newLen = 0;
for (int i = 0; i < arr.length; i++) {
if (i + 1 == arr.length || arr[i] != arr[i + 1]) {
arr[newLen++] = arr[i];
}
}
return Arrays.copyOf(arr, newLen);
}
static class SuffixArray {
int[][] classes;
String s;
int maxH;
SuffixArray(String s) {
this.s = s;
maxH = 0;
while ((1 << maxH) <= s.length()) maxH++;
classes = new int[maxH][];
for (int h = 0; h < maxH; h++) {
classes[h] = new int[s.length()];
}
for (int i = 0; i < s.length(); i++) {
classes[0][i] = s.charAt(i) - 'a';
}
for (int h = 1; h < maxH; h++) {
long[] values = new long[s.length() - (1 << h) + 1];
int valuesLen = 0;
for (int i = 0; i + (1 << h) <= s.length(); i++) {
int leftPart = classes[h - 1][i];
int rightPart = classes[h - 1][i + (1 << (h - 1))];
long curValue = ((long)leftPart << 30) ^ rightPart;
values[valuesLen++] = curValue;
}
values = unique(values);
for (int i = 0; i + (1 << h) <= s.length(); i++) {
int leftPart = classes[h - 1][i];
int rightPart = classes[h - 1][i + (1 << (h - 1))];
long curValue = ((long)leftPart << 30) ^ rightPart;
classes[h][i] = Arrays.binarySearch(values, curValue);
}
}
}
int getLCP(int i, int j) {
int res = 0;
for (int h = maxH - 1; h >= 0; h--) {
if (i + (1 << h) <= s.length() && j + (1 << h) <= s.length() && classes[h][i] == classes[h][j]) {
res += (1 << h);
i += (1 << h);
j += (1 << h);
}
}
return res;
}
}
@Override
public void run() {
InputReader in = new InputReader(System.in);
PrintWriter out = new PrintWriter(System.out);
int n = in.nextInt();
String s = in.next();
int m = in.nextInt();
String t = in.next();
int x = in.nextInt();
int[][] dp = new int[x + 1][n + 1];
for (int i = 0; i <= x; i++) {
for (int j = 0; j <= n; j++) {
dp[i][j] = Integer.MIN_VALUE;
}
}
String q = s + "#" + t;
SuffixArray sarr = new SuffixArray(q);
dp[0][0] = 0;
for (int cnt = 0; cnt <= x; cnt++) {
for (int prefS = 0; prefS <= n; prefS++) {
if (dp[cnt][prefS] == Integer.MIN_VALUE) continue;
//System.err.println("cnt = " + cnt + ", prefS = " + prefS + ", value = " + dp[cnt][prefS]);
if (prefS + 1 <= n && dp[cnt][prefS + 1] < dp[cnt][prefS]) {
dp[cnt][prefS + 1] = dp[cnt][prefS];
}
if (cnt + 1 <= x) {
int prefT = dp[cnt][prefS];
int lcp = sarr.getLCP(prefS, prefT + n + 1);
if (dp[cnt + 1][prefS + lcp] < prefT + lcp) {
dp[cnt + 1][prefS + lcp] = prefT + lcp;
}
}
}
}
boolean ok = false;
for (int cnt = 0; cnt <= x; cnt++) {
if (dp[cnt][n] == m) {
ok = true;
}
}
out.println(ok ? "YES" : "NO");
out.close();
}
public static void main(String[] args) {
new Thread(null, new Main(), "1", 1L << 28).run();
}
}
Tutorial is loading...
First accepted Div1: 00:16:33 webmaster
First accepted Div2: 01:12:52 Nisiyama_Suzune
Author's solution
const int maxn = 105;
vector < pair < int, int > > edge[maxn];
int used[maxn];
int from[maxn];
int where[maxn];
ld dist[maxn];
void dfs( int v, ld prevTime ) {
used[v] = true;
int sz = edge[v].size();
ld bestTime = 2.0L / sz;
ld nextTime = prevTime + bestTime;
if ( nextTime >= 2.0L )
nextTime -= 2.0L;
for ( int j = 0; j < sz; j++ ) {
int id = edge[v][j].f;
int to = edge[v][j].s;
if ( used[to] )
continue;
ld toTime;
if ( nextTime <= 1.0L ) {
from[id] = to;
where[id] = v;
dist[id] = 1.0L - nextTime;
toTime = nextTime + 1.0L;
} else {
from[id] = v;
where[id] = to;
dist[id] = 2.0L - nextTime;
toTime = nextTime - 1.0L;
}
dfs( to, toTime );
nextTime = nextTime + bestTime;
if ( nextTime >= 2.0L )
nextTime -= 2.0L;
}
}
int main()
{
int n;
scanf ( "%d", &n );
for ( int j = 1; j < n; j++ ) {
int u, v;
scanf ( "%d%d", &u, &v );
edge[u].pb( mp( j, v ) );
edge[v].pb( mp( j, u ) );
}
dfs( 1, 0 );
printf( "%d\n", n - 1 );
for ( int j = 1; j < n; j++ ) {
printf( "%d %d %d %d ", 1, j, from[j], where[j] );
cout << fixed << setprecision( 10 ) << dist[j] << endl;
}
}










how do u prove that the solution to D is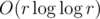 ?
?
When u are processing dp, it seems like depending on how many prime factors i has.
So i think it should be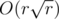 ?
?
No, because you only need to choose the smallest prime factor each time.
If you go one by one and factor every number from l to r, the running time is indeed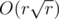 . However, to speed this up, we instead use a Eratosthenes sieve-like approach: from l to r, look at all the multiples of 2, then all the multiples of 3, then all the multiples of 5, etc.. The running time is thus
. However, to speed this up, we instead use a Eratosthenes sieve-like approach: from l to r, look at all the multiples of 2, then all the multiples of 3, then all the multiples of 5, etc.. The running time is thus 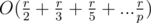 which was proven by Euler (?) to be approximated by
which was proven by Euler (?) to be approximated by 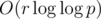 .
.
Why is this solution giving tle whereas this passes.
In first soln I am storing all the distinct primes of a no than calculating the ans whereas in second soln I am dividing by smallest prime factor each time.
I also calculated the total no of times the loop is executed in both the solutions and the first soln has less execution.
Can anyone help on this ?
Would you mind sharing why most people got E WA'd by using
dp[sprefix][xcnt][flag]? I tried to come up with a counterexample but nevertheless failed.Try this sample. Some of the solutions, that get WA24, fail on this test:
10baaabbbcac5babbc2(The correct answer is "YES" as you can see).
I see. My friend has also made a hack to my own program:
Many thanks!
Thanks! This was a saviour
Can anyone please tell me what I did wrong on problem C so I got WA on test 58 :(
28220911
The question asks you to find the sum of cost of vouchers whose intervals don't intersect. You don't entertain that possibility. You just find the minimum cost of the required interval length whose starting point is before it, but that doesn't guarantee that they don't intersect.
For eg, Your code fails on:
Answer is -1 whereas your code prints 2. Your code takes two intersecting intervals which should not be the case.
Can anybody help me please ? :)
C solution
it gives 3 instead of 2 on foll test case:- 3 6 1 3 1 4 6 2 7 9 1 Mistake in ur code is that when u binary search,according to your code you should check all possible coupons for whom st>last and time==left. but say if a[mid] follows the condition it may be possible that a[mid+1] also follows these 2 conditions and furthermore may have lower cost causing the error.But u change r to mid-1 hence never searching for lower cost in indices greater than mid.
Ah, thanks a lot. :D
Then, can I edit my approach or this solution is basically wrong?
Well it seems to me that ur soln is wrong and atleast it is not the best approach. You may see my solution if needed - http://codeforces.com/contest/822/submission/28246016
I saw your solution, but I was able t understand your logic, plz example it to me. I tried by using map but getting tle.
Maybe bcoz map is slower u may be getting tle. What i am doing is for each i, for each cupoun that ends on day i we will check for best matching cupoun that starts after i and of duration x — duration of given coupon which is stored in ans array
Can anyone please tell me what I did wrong on problem C so I got WA on test 58 :(
28220911
It's embarrassing although my solution for D passed I couldn't prove it before reading the editorial. Thanks!
I dont know why i got E wa on test 172,which is the last case. Can any one help me??? My submission
Oops,i got wa because of my hash,mod 264 is stupid
Could you explain why?
I also got WA on test 172 :( Can you help me with this ? 28386238
For people who are still struggling or trying to understand problem c solution and not able to understand editorial (like me :p ), i want to explain it since i solved it now.
Brute force solution is
O(n^2)which i think everyone can get. We wantO(n)orO(nlogn).Approach:
1)store interval
{l,{r,cost}}invector<pair<int,pair<int,ll>>>a2) First sort the intervals
vector<pair<int,pair<int,ll>>>awrt left point.3) Iterate over vector
aand store duration in another vectorvector<pair<int,int>>min_value[N](It contains left point and cost). This vector will contain information about all intervals with a specific duration.Good thing ismin_value[d]will contain interval information in sorted wrt left point (isn't it ?)4) Now we will find our answer similar to our bruteforce approach. Bruteforce is to iterate over all intervals , and for each interval we will take
O(n)to find min_cost. We are trying to reduce thisO(n)toO(logn)to make our solutionO(n logn).5) So start iterating , choose first interval , we know it's duration
d, ourneed = x - d;we have intervals in our vectormin_value[need]which is sorted wrt to left point , we want to find that index inmin_value[need]which has it's left point greater than current interval's right point.we can find that using binary search and obtain minimum cost. There will be many possible interval satisfying our interval condition , we can choose any with min_cost , so we also need to precompute min_cost in all intervals ahead of that index (similar to prefix sum)
Here is my solution , see this everything will make sense.
your explanation helped :) But one thing is not clear to me. Can you explain this to me?
There will be many possible interval satisfying our interval condition , we can choose any with min_cost , so we also need to precompute min_cost in all intervals ahead of that index (similar to prefix sum)
how and why does this work? thanks :)
EDIT: I got it now. :D
For
Problem D, this code, gives TLE on test 18, I think it has the same time complexity as intended. Could anyone help me with this. Thanks.Your code's complexity is
R.log(R)whereas the intended complexity isR.log(log(R))No need to divide x by all its factor to find dp[x]. Just divide it by its smallest prime factor.
dp[x] = dp[x/sp[x]] + (sp[x]*(sp[x]-1))/2will work, sp[x]: smallest prime factor of x.Preprocessing the sp array is
O(R.log(log(R))and the calculation of dp will beO(R).Melnik, What if for C we consider the following solution:-
1) We sort the vouchers in increasing order of the cost. O(nlogn)
2) Then for each voucher Vi we find a Vj (j>i) such that the intervals don't intersect, and such that duration of the Vi+Vj is x. We return the first Vj we find satisfies this conditions.Time complexity — O(n^2)
Is the above solution conceptually correct?(Other than having poor efficiency)
Yes
But it is giving wrong answer on pretest 4. You can check my submission — 28227628
You are not checking further for any Vi as soon as you find Vi+Vj==x. It can be possible that for next Vi you will find appropriate Vj such that total cost is less compared to previous.
I used the same logic as you described and it gives timeout in 4th test case. Here is the link -> 28221981
No, it's wrong. Try this case:
4 5
1 3 4
1 2 5
3 5 6
4 5 8
Your answer = 12
Actual answer = 11
In D, "So, we proved that all di should be prime", how is it proved bcz spliting a composite number into 2 gives less comparisons?? can someone explain this
"how is it proved bcz spliting a composite number into 2 gives less comparisons"
You said it yourself: splitting is cheaper. So we should split, as much as we can -> we have split it into primes.
thanks, got it!!
Hi johnLate, Dont you think then even must be split in only pair of twos and odd with a triplet and all other into pair. This should result in minimum cost . However I am not getting same answer. Thanks
Each group of a stage must have the same size. For example, you can split 15 into 3,3,3,3,3 or 5,5,5. But you can not split it into 2,2,2,2,2,2,3 or something like that.
Example for n=15: In the first stage split into 5 groups of x=3 girls, do
x(x-1)/2comparisons for each group, then solve the problem for the resulting 5 girls.f(15) = 5 * 3(3-1)/2 + f(5)[Note: It isf(n) = n/x * x(x-1)/2 + f(n/x), it is NOTf(n) = n/x * f(x) + f(n/x)]O (n) solution for C 28236057
Can anybody please help me find out what's wrong with my solution for problem C?
28233171
For each value of i, we may have many possible values of ind but we need to find one for which cost is minimum. You are just checking the first possible value of ind only!
Thanks for the reply! However, I first sort all the vouchers according to the cost in ascending order and then I pick the first voucher. So, the first one has minimum cost.
Say if m does not satisfies the condition, you take l = m+1 ( rembeber that if duration of coupon is greater than or equal to x than we can simply ignore them right from the start hence second condition really never makes sense as we can assume all coupon have duration less than x!) . But it may be possible that m-1 may satisfy the condition or similarly any value less than m even though m may not satisfy the condition! In your soln, You need to find out smallest index between l and r that satisfies the 2 condition!
Can someone explain author's solution in C. Why 2 types of queries {-1,1} and why updating bestcost online like this works.
Firstly notice that we are adding both 'l' and 'r' to queries vector as this will help us refrain from intersecting intervals. Then on the other hand we have to also keep track of whether the value is the start of interval or end of the interval, so {-1,1} are used.
The main thing to see is that bestCost is updated when 'r' is found and ans is updated when 'l' is found.This thing makes sure that an interval doesn't uses bestCost from any other intersecting interval before "ans" is updated on 'l'.
HELP!!! How to FORGIVE!!
Haha, funny bug :D
I'll fix it soon.
Can somebody help regarding my solution for D. It's giving runtime error on test 1. I think there is a problem with my sieve because after commenting that program runs correctly on test 1. But my sieve function looks good to me. 28250621
Runtime error cause you are using too much memory! And even if you decrease the memory complexity, you'll still get tle anyway.
See I submitted 2 solutions. With sieve 28250621 and without sieve 28250581. They both almost use same amount of memory but sieve one is giving RTE.
Fix rep(i,2,NMAX) to rep(i, 2, NMAX — 1) and for(j=2;i*j<=NMAX;j++) to for (j=2;i*j<NMAX;j++)
Div 2 C wrong ans test case 25. Any help?
http://codeforces.com/contest/822/submission/28250623
DIV2 wrong answer on test 13, but I really think it is right(binary search for len of every voucher). Anyone help? http://codeforces.com/contest/822/problem/C
sorry... the problem is C. I forget that...
For C what I did was made a array of vectors of duration. Then while traversing the queries I know that the required duration is x-(r[i]-l[i]+1) and in duration vector I find the starting position with binary search and apply RMQ. I got runtime error on test 3. Is there anything wrong with this approach?
Can anyone help me with hashing to find lcp in problem E? Do we precalculate hash values and then in every DP state find it in O(logN) — only binary search? Please help.
http://codeforces.com/contest/822/submission/28265538 I managed to solve it. Learned a bit more about hashing and realised all I need is rolling hash and in O(1) I can easily get hash of some segment. So, per dp state only log(n) is needed to binary search for max lenght.
"But if we divide this stage into two new stages, then number of comparisons is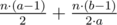 " .
" .
how do we get this equation ?
In first stage: There are "n/a" groups of a elements each. So comparisons are (n/a)*(a)*(a-1)/2 = n*(a-1)/2
For Second stage: There are "(n/a)/b" groups because from first stage "n/a" elements go ahead. So comparisons are (n/(a*b))*(b)*(b-1)/2 = n*(b-1)/(2*a)
Can somebody help in finding why my Div2 C is giving wrong answer.. I know my solution will give TLE but why is it giving WA.. I need to know,what's wrong with the approach,I already know it's not efficient,but I cant figure out why WA in testcase 12..
SOLUTION
My approach : I created a vector that contains duration of vacation,start time,end time and cost in that order.. Next,I sorted it... Next,starting with i = 0 , from the beginning of this vector,I find the required duration (x — duration[i]) I use lower_bound to search for this value compare all such elements having the same duration (x — duration[i]) I understand it will yeild TLE,but WA,I can't understand..Please help!!
Could someone help me with my solution on problem C? Why is it failing on test 3?
I sort segments (l, r) by left bound, then while being in segment i, I update mincost with all segments with r_k < l_i which have not been used for updating yet.
Submission: http://codeforces.com/contest/822/submission/28257988
UPD: found failing test case:)
my solution: -1 correct answer: 2
Can anyone help me with my code? I got Runtime error on problem C but I don't know why. Thank you very much! http://codeforces.com/contest/822/submission/28261279
In Problem C, I'm really amazed no one mentioned the O(Max(li, ri)) for i = 1 → n greedy solution!
The solution is only possible due to the low range of li, ri which is less than 2·105
We simply use this fact to store the vector of pairs of {ri, costi} at index li in an array called left , and do the complement of this in another array (i.e. store the vector of pairs of {li, costi} at index ri in an array called right)
Then we loop for every i = 1 → Max(li, ri) and fix our index i to be the left bound and check for every pair j at left[i] to see if we have encountered a non intersecting segment before it that has the length X - (left[i][j].r - i + 1) in an array called best for example and minimize our cost by the current which is the cost of the current pair left[i][j].cost and whatever was saved in the complementary segment length in our array best[X - (left[i][j].r - i + 1)]
After we have processed the fixed left index, let's see if there's a segment has its right index at this same index i, if so we need to minupdate the value of its length in our array best to use it in the future at further indices, and this way we're sure we can never have intersecting segments, because we query first and then update.
I hope I haven't made it much worse than the obvious O(n·log(n)) which could be due to binary searching or using a map/set to store higher ranges.
All in all, here's the link to my submission for further detail -> 28237414
Update: Never mind! My brain did not work until I wrote the comment!
I was going through the submission 28257135 for problem E. I was wondering what is the time complexity of below two statements.
1.
2.
regarding problem D in the point of all di should be prime:
it can also be thought of as: suppose number d with n1*n2 = d (where n1 and n2 >= 2 and are prime), without splitting, comparisons made are: n1n2(n1n2 — 1) / 2. with splitting, comparisons made are: n2n1(n1 — 1)/2 + n2(n2 — 1)/2 (supposing that d is splitted to n2 groups with n1 participants in each group), now subtract the second equation from the first one : 0.5((n1n2)^2 — n2(n1^2) — n2^2 + n2), rewriting the expression: 0.5n2((n1^2) * (n2 — 1) — (n2 — 1)), rewriting again: 0.5n2(n2 — 1)(n1^2 — 1), which is clearly greater than 0, so the number of comparisons made in the first equation is larger than those made in the second equation.
I understood the problem D. However, how can we come up with the idea "all di should be prime" ? Thanks you.
Observing.Try to calculate f(16), f(20)...If u had experience in olympiad maths it would be easier, because in maths many times you need to observe something, to see a pattern. So, just calculate few f-values and you will see that optimal is to choose di as smallest possible, but since they need to divide total number of people in current stage, they must be primes.
Its important to mention that i solved a problem without this observation, only bottom up DP. Thats why solution passed in 1450 ms while 1500 ms was limit, so i was lucky.
Can anyone teach me how to prove "you can prove the fact that we should split the girls into groups by prime numbers in the order of their increasing" in problem D.Thanks a lot :)
just suppose a and b are two distinct prime factors of n. The number of comparisions that you want to minimize is given by the recursion formula:
By this you can imagine the expansion for all the factors of n. For two different prime factors a and b you get to choose if a is bigger or smaller than b.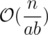 will be the same no matter the choice. So just analise the first part of the expression, the
will be the same no matter the choice. So just analise the first part of the expression, the 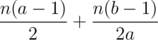 . Imagine all pairwise choices for a and b among all prime factors of n, by proving that choosing a<b is better (that is, between the two options choose, for a, the smaller one), you can notice that among all pairwise choices only the smallest avaible factor won't lose to any other factor, so, since there must be a choice that minimizes (or at least equals the minimum), it must be the current smallest factor avaible.
. Imagine all pairwise choices for a and b among all prime factors of n, by proving that choosing a<b is better (that is, between the two options choose, for a, the smaller one), you can notice that among all pairwise choices only the smallest avaible factor won't lose to any other factor, so, since there must be a choice that minimizes (or at least equals the minimum), it must be the current smallest factor avaible.
So what is left is to prove that for a set of two numbers, choosing for a the smaller one minimizes the expression: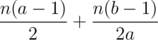
That is the same as, given two prime numbers a and b such that a<b prove that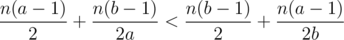 . You can rearrenge the last inequality to get ab(b - a) + (a - b)(a + b) + b - a > 0 which is true because b>a and both a and b are bigger than 1 because they are primes so, for sure |ab(b - a)| > |(a - b)(a + b)| because ab > (a + b) which concludes the proof.
. You can rearrenge the last inequality to get ab(b - a) + (a - b)(a + b) + b - a > 0 which is true because b>a and both a and b are bigger than 1 because they are primes so, for sure |ab(b - a)| > |(a - b)(a + b)| because ab > (a + b) which concludes the proof.
Thank you. Maybe I fail to get the point... I thought you only prove that if the pair a,b is given (a<b), then it's wiser to divide people into n/a groups. But what if there are four prime factors of n, a,b,c,d(a<b<c<d), and it's better to choose b,c as the pair first instead of a,b or a,c or a,d? Can you prove that this situation is impossible? Sorry for my poor English...
You are right. I did not prove why the solution must be greedy and, in fact, I do not know how to do that. An ideia to why this works is, since the next values will be divided by ab (the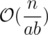 part) what is most important to minimize is the current value not divided.
part) what is most important to minimize is the current value not divided.
Anyway thank you:)
can someone please post a noob's solution for problem E? really couldn't understand a thing...
You can refer to my submission here. Tried to make it as clear as possible. (:
http://codeforces.com/contest/822/submission/28289280
by noob's solution I meant, noob's explanation :P... can you help with that? really having a hard time to figure out how to proceed...
Okay so you need to find if string S of length l1 can be broken by maximum x cuts into pieces that can be joined together to form string T of length l2. Assume that the strings are 1-indexed. dp[i][j] stores the maximum prefix of T that can be obtained from length j of string S after i cuts. So obviously, we need to see if there exists a value of i that is less than or equal to x such that dp[i][l1]=l2. Now assume that you have dp[i][j]=t1. That means after i cuts and length of j from string S, we can obtain the first t1 characters of string T. Now, two transitions are possible. Either the j+1'th character of string S matches with t1+1'th character of string T, resulting some length of their prefixes matching, or those characters are not equal.
If the characters are equal, we can binary search + hashing to find the LCP (Longest Common Prefix) of string S from j+1...l1, and string T from t+1...l2. Suppose the LCP is t2. Then, the transition dp[i+1][j+t2]=max(dp[i+1][j+t2],dp[i][j]+t2). (i+1, j+t2 must lie within bounds)
If the characters aren't equal, then dp[i][j]=max(dp[i][j],dp[i][j+1]) because the first j+1 characters of string S can give the same answer as the first j characters.
Hope this explains it. (:
I notice that some of the current AC solutions for Problem E use greedy strategy and I think it is wrong. For example, 28272853. I was wondering if there is a chance to open hack and rejudge. Hope the solutions won't mislead future coders. I got a test case to turn these solutions into WA.
The answer should be YES but these solutions output NO. Thanks.
guys can someone gives me a simplified test case according to test case 7 in Div2 C problem :( my code fails and has got WA on test case 7 :/ this is my code here
On codeforces we do not have access to the full test case, but what you can do is when you detect the problematic test case (that is, in your case when n == 200000 and x == 114451) you print whatever parameter you need to debug. Your code is outputing a value smaller then the answer from the jury, so your two choices for the 2 vouchers shoud be invalid, that is, they intersect or something like this, just print it to check.
In the author's solution for 822C - Hacker, pack your bags!, why do we have to add two types of queries? Isn't the first type enough to handle all cases?
For those who use hash for E and got wrong answer in test case 172
unsigned long long is hacked, u have to modulo something else.
I use an O(r*log(r)) algorithm and get Accepted as well. Instead of enumerating all primes, I use all factors to update the answer.
i am getting runtime error for case 2 but when i am running my code on my pc for case 2, i am getting correct answer. Here is the link to my submission: http://codeforces.com/contest/822/submission/28796938
Very strange TL in div2 D, I wrote solution with the same idea as in editorial, but it got TLE with 1.8 sec in worst case (l = 2, r = 5·106). I replace some long long variables with int (it always helps a bit), but got 1.575 sec in worst case.
So it would be smarter just to make TL = 2 sec and not to make people find small extra optimizations for their code (main solution idea is enough, isn't it?).
http://codeforces.com/contest/822/submission/34284404 can anyone tell me why i am getting WA on test case 19? it seems okay to me
Can anyone explain the dp states along with transitions of problem E div2, unable to get it from editorial.
In Div2 C problem, Why we can't sort the vouchers by their right borders?
I think there exists a greedy approach to solve Div2 D. Instead of using dp to compute f(n), we can split n people into groups each containing spf(n) people, where spf(n) denotes the smallest prime factor of n. https://codeforces.com/contest/822/submission/90345138