I've been recently thinking about this problem:
Given array of n integers and q queries( l, r pairs ). For each query you need to count number of inversions( i, j pairs such that i < j and a[i] > a[j] ) in subarray from l to r. And you have to answer the queries online(you're not given all queries beforehand).
I was able to come up with a solution that i'd describe below, but I'd like to know if it's possible to solve the problem with better complexity.
So, my solution:
1) preprocessing
Let's divide our array into sqrt(n) blocks, each sized sqrt(n), and merge-sort elements inside each, counting number of inversions in it. Then, for each pair of blocks, count number of inversions such that first element lies within first block and second lies within second block. We can do this using binary search, because each block is sorted already. After that, for each sqrt-block-range( [l, r] range such that l is a left border of one block and r is a right border of other block ) we'd find number of inversions in it by summing precalculated values( inversions in each block and inversions in pairs of blocks). There are around n pairs and ranges so we can do all preprocessing in O(n * sqrt(n) * log(n)). We also need to build merge-sort tree on the array for queries.
2) queries
We already know answer for sqrt-block-range that lies within query range. Then we just need to count inversions that include elements outside sqrt-block-range. There no more than 2 * sqrt of such elements, so we can do this with binary search in merge-sort tree in O(sqrt(n) * log^2(n)), or in O(sqrt(n) * log(n)) with partial cascading.
Overall complexity: O((n + q) * sqrt(n) * log(n)) with partial cascading.
So what are your thoughts, can it be solved faster?
P.S. Sorry for my poor English.











Auto comment: topic has been updated by madn (previous revision, new revision, compare).
Edit: I missed something so this was wrong XD.
It is O(N lg N) for each query, because you merge sorting a segment of array, is not it?
yeah I had a mistake in my solution, I didn't mean to do it repeatedly for every query, but I definitely missed something. oops :P
yes, it can be (with something of classic sqrt-decomp and MO's algo)
1) divide array to blocks of size
2) calculate answers for all segments [L, r] where L — start of block and r — arbitrary index. Similary for all segments [l, R], R — end of the block. It needs two tables with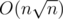 memory.
memory.
3) answer on query [l, r]: find L and R such l ≤ L ≤ R ≤ r. preanswer is invs[L][r] + invs[l][R] - invs[L][R]. remains add inversions i, j such l ≤ i < L ≤ R < j ≤ r (on corners). it can be done with two pointers if you have sorted elements on each block.
So, 2) can be done in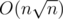 time (yes i not described it, try to think about dynamic prog) and 3) in
time (yes i not described it, try to think about dynamic prog) and 3) in 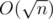 per query
per query
I liked your approach to the problem very much,
but as for doing step 2 in O(n.sqrt(n)) time, I have been thinking hard about it and I have not figured out how can it be done ??
normal counting inversions in array using BIT or merge sort requires O (n.logn) so can you please describe how your suggested DP approach works in more detail, or give me some hints to think about it
Thanks in advance
ok, hint:
invs[L,r] = invs[L,r-1] + invs[L+D,r] - invs[L+D,r-1] + azazaazazais inversions ofa[r]and element from blockLby two pointers for sorted
aand for sorted block you can calculate eachazazain $$$O(nlogn + n \sqrt n)$$$ totalAhhhh, I see
I think I almost got it now :).
but just to make sure I got it all correctly,
L+Dis the First Block that Comes after BlockL,azazais how many element in blockLmake an inversion witha[r]which lie outside of block L, right ??so if we have sorted block
Lpreviously as you said, then we can getazazausingupper_boundon BlockLinO(log(sqrt(n))for a little better complexity.so the total complexity of the overall preprocessing should be
O(n.sqrt(n).log(sqrt(n))), am I right ??yes, right
but total must be $$$O(n \sqrt n)$$$
sort
L-th blockiterate each element in
aafterL-th block in increasing orderwith second pointer in block you can achive needed count of inversions
"iterate each element in
aafterL-th block in increasing order"does this means that I have to sort the part of the array after the current
LBlock for each block while keeping their indices, right??so actually we will have one extra
n.sqrt(n)array for keeping theazazavalues too .while searching more about this, I found this solution: https://stackoverflow.com/a/21790297 which is very similar to yours, but the thing is that he said the complexity is
O (n.sqrt(n).log(n)).which I think is inevitable, even if we use two pointers to calculate
azaza, we still have to sort the " after L-th block in increasing order" part of the array, which will add the log(n) to our complexity.I have been thinking hard about it since yesterday, but I can't see yet how it can achieved in just
O(n.sqrt(n):(Is there a trick which can help you to traverse the
a[r]'s in increasing order without resorting them for each BlockL??Sort whole array once
Iterate only on necessary elements
can step 3 be done in O(sqrt(n))?
i can't think of it, if anyone used this idea, please help me out
Direct me which phrases you didn't understand?
Related:
https://discuss.codechef.com/questions/38033/iiti15-editorial
https://www.hackerearth.com/practice/data-structures/advanced-data-structures/fenwick-binary-indexed-trees/practice-problems/algorithm/sherlock-and-inversions/editorial/