This short article is mainly focused on the linear sieve and its various applications in competitive programming, including a brief introduction on how to pick out primes and a way to calculate multiple values of multiplicative functions.
Sieve of Eratosthenes
While this name may sound scary, the sieve of Eratosthenes is probably the simplest way to pick out all the primes in a given range from 1 to n. As we already know, one of the properties that all primes have is that they do not have any factors except 1 and themselves. Therefore, if we cross out all composites, which have at least one factor, we can obtain all primes. The following code demonstrates a simple implementation of the said algorithm:
std::vector <int> prime;
bool is_composite[MAXN];
void sieve (int n) {
std::fill (is_composite, is_composite + n, false);
for (int i = 2; i < n; ++i) {
if (!is_composite[i]) prime.push_back (i);
for (int j = 2; i * j < n; ++j)
is_composite[i * j] = true;
}
}
As we can see, the statement is_composite[i * j] = true; crosses out all numbers that do have a factor, as they are all composites. All remaining numbers, therefore, should be prime. We then check for those primes and put them into a container named prime.
Linear sieve
It can be analyzed that the method above runs in  complexity (with the Euler–Mascheroni constant, i.e.
complexity (with the Euler–Mascheroni constant, i.e. 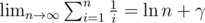 ). Let us take a minute to consider the bottleneck of such sieve. While we do need to cross out each composite once, in practice we run the inner loop for a composite multiple times due to the fact that it has multiple factors. Thus, if we can establish a unique representation for each composite and pick them out only once, our algorithm will be somewhat better. Actually it is possible to do so. Note that every composite q must have at least one prime factor, so we can pick the smallest prime factor p, and let the rest of the part be i, i.e. q = ip. Since p is the smallest prime factor, we have i ≥ p, and no prime less than p can divide i. Now let us take a look at the code we have a moment ago. When we loop for every i, all primes not exceeding i is already recorded in the container
). Let us take a minute to consider the bottleneck of such sieve. While we do need to cross out each composite once, in practice we run the inner loop for a composite multiple times due to the fact that it has multiple factors. Thus, if we can establish a unique representation for each composite and pick them out only once, our algorithm will be somewhat better. Actually it is possible to do so. Note that every composite q must have at least one prime factor, so we can pick the smallest prime factor p, and let the rest of the part be i, i.e. q = ip. Since p is the smallest prime factor, we have i ≥ p, and no prime less than p can divide i. Now let us take a look at the code we have a moment ago. When we loop for every i, all primes not exceeding i is already recorded in the container prime. Therefore, if we only loop for all elements in prime in the inner loop, breaking out when the element divides i, we can pick out each composite exactly once.
std::vector <int> prime;
bool is_composite[MAXN];
void sieve (int n) {
std::fill (is_composite, is_composite + n, false);
for (int i = 2; i < n; ++i) {
if (!is_composite[i]) prime.push_back (i);
for (int j = 0; j < prime.size () && i * prime[j] < n; ++j) {
is_composite[i * prime[j]] = true;
if (i % prime[j] == 0) break;
}
}
}
As is shown in the code, the statement if (i % prime[j] == 0) break; terminates the loop when p divides i. From the analysis above, we can see that the inner loop is executed only once for each composite. Hence, the code above performs in O(n) complexity, resulting in its name — the 'linear' sieve.
Multiplicative function
There is one specific kind of function that shows importance in the study of number theory — the multiplicative function. By definition, A function f(x) defined on all positive integers is multiplicative if it satisfies the following condition:
For every co-prime pair of integers p and q, f(pq) = f(p)f(q).
Applying the definition, it can be shown that f(n) = f(n)f(1). Thus, unless for every integer n we have f(n) = 0, f(1) must be 1. Moreover, two multiplicative functions f(n) and g(n) are identical if and only if for every prime p and non-negative integer k, f(pk) = g(pk) holds true. It can then be implied that for a multiplicative function f(n), it will suffice to know about its representation in f(pk).
The following functions are more or less commonly used multiplicative functions, according to Wikipedia:
- The constant function I(pk) = 1.
- The power function Ida(pk) = pak, where a is constant.
- The unit function ε(pk) = [pk = 1] ([P] is 1 when P is true, and 0 otherwise).
- The divisor function
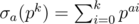 , denoting the sum of the a-th powers of all the positive divisors of the number.
, denoting the sum of the a-th powers of all the positive divisors of the number. - The Möbius function μ(pk) = [k = 0] - [k = 1].
- The Euler's totient function φ(pk) = pk - pk - 1.
It is interesting that the linear sieve can also be used to find out all the values of a multiplicative function f(x) in a given range [1, n]. To do so, we have take a closer look in the code of the linear sieve. As we can see, every integer x will be picked out only once, and we must know one of the following property:
- x is prime. In this case, we can determine the value of f(x) directly.
- x = ip and p does not divide i. In this case, we know that f(x) = f(i)f(p). Since both f(i) and f(p) are already known before, we can simply multiply them together.
- x = ip and p divides i. This is a more complicated case where we have to figure out a relationship between f(i) and f(ip). Fortunately, in most situations, a simple relationship between them exists. For example, in the Euler's totient function, we can easily infer that φ(ip) = pφ(i).
Since we can compute the function value of x satisfying any of the above property, we can simply modify the linear sieve to find out all values of the multiplicative function from 1 to n. The following code implements an example on the Euler's totient function.
std::vector <int> prime;
bool is_composite[MAXN];
int phi[MAXN];
void sieve (int n) {
std::fill (is_composite, is_composite + n, false);
phi[1] = 1;
for (int i = 2; i < n; ++i) {
if (!is_composite[i]) {
prime.push_back (i);
phi[i] = i - 1; //i is prime
}
for (int j = 0; j < prime.size () && i * prime[j] < n; ++j) {
is_composite[i * prime[j]] = true;
if (i % prime[j] == 0) {
phi[i * prime[j]] = phi[i] * prime[j]; //prime[j] divides i
break;
} else {
phi[i * prime[j]] = phi[i] * phi[prime[j]]; //prime[j] does not divide i
}
}
}
}
Extension on the linear sieve
Well, it might not always be possible to find out a formula when p divides i. For instance, I can write some random multiplicative function f(pk) = k which is difficult to infer a formula with. However, there is still a way to apply the linear sieve on such function. We can maintain a counter array cnt[i] denoting the power of the smallest prime factor of i, and find a formula using the array since 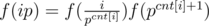 . The following code gives an example on the function I've just written.
. The following code gives an example on the function I've just written.
std::vector <int> prime;
bool is_composite[MAXN];
int func[MAXN], cnt[MAXN];
void sieve (int n) {
std::fill (is_composite, is_composite + n, false);
func[1] = 1;
for (int i = 2; i < n; ++i) {
if (!is_composite[i]) {
prime.push_back (i);
func[i] = 1; cnt[i] = 1;
}
for (int j = 0; j < prime.size () && i * prime[j] < n; ++j) {
is_composite[i * prime[j]] = true;
if (i % prime[j] == 0) {
func[i * prime[j]] = func[i] / cnt[i] * (cnt[i] + 1);
cnt[i * prime[j]] = cnt[i] + 1;
break;
} else {
func[i * prime[j]] = func[i] * func[prime[j]];
cnt[i * prime[j]] = 1;
}
}
}
}
Example problems
The Embarrassed Cryptographer
Solution: Simply applying the linear sieve will be enough.
Farey Sequence
Solution: Notice that Δ F(n) = F(n) - F(n - 1) is multiplicative and Δ F(pk) = pk - pk - 1. Then the linear sieve will come in handy to solve the problem.











I don't understand anything. But it looks like something useful so upvote for you.
I understand your comment. So.. upvote for you
@Nisiyama_Suzune do you have any origin reference for this linear sieve? It's amazing it's not well known (as far I know) in the competitive programming world.
It would appear that this technique is established in 1978 by David Gries and Jayadev Misra at the communication of the ACM. They had a paper here. However, I was unable to purchase it so I cannot determine whether it is true.
Yes I have just checked :) Good source...
A linear sieve algorithm for finding prime numbers *-* great post.
Thanks for the compliment:)
Can someone explain why are we doing
if (i % prime[j] == 0) break;Finally I understood it , Once we reach a number
i * prime[j]wherei % prime[j] == 0we know thati * prime[j + 1]will also haveprime[j]as the smallest prime divisor.You are right :)
I got stuck on this too. For future reference it is a special case of the fact that when a|(bc) and gcd(a,c)=1, then a|b.
hello there,
i usually write sieve in this style:
isn't the amortized complexity of this algorithm O(n)? or do i understand something wrong?
Based on my knowledge, only crossing out even numbers first does not make a sieve O(n), so I doubt its correctness on complexity. For instance, 105 will be visited multiple times (for 3, 5 and 7) in your code. Therefore, I think your code still performs in . However, I do think there is not too much difference between O(n) and
. However, I do think there is not too much difference between O(n) and  in sieves. The reason why I introduced the algorithm is mainly that it can help to compute the multiplicative functions, where other sieves are less likely to do so.
in sieves. The reason why I introduced the algorithm is mainly that it can help to compute the multiplicative functions, where other sieves are less likely to do so.
That code in particular is O(nloglogn) since it uses the sum of inverse of primes which is bounded by O(loglogn).
In your Euler's function, when X = iP and P does not divide i, shouldn't it be
phi[i * prime[j]] = phi[i] * phi[prime[j]]? Since j is only the index of the prime.Awesome blog btw. Keep on with the math notes!
Awww...My bad. Will fix it, sorry!
In the code for Phi function :
for (int j = 0; j < prime.size (); ++j) {It should bej < prime.size() && i*prime[j] < nReally Awesome blog :) ! Thanks, And Keep Writing
In the Extension on the linear sieve, in the
i%prime[j]==0condition, shouldn't it befunc[i * prime[j]] = func[i / pow(prime[j],cnt[i])] * func[pow(prime[j],cnt[i] + 1)]?How to solve the easy problem!! The Embarrassed Cryptographer
Precompute all primes till 106, then for every prime less than L check if it divides K. O(|K| * pi) for each test case where pi is the count of primes less than L.
Yes but ain't 4 <= K <= 10^100?, how can I do that in c++ without implementing my own BigNum divide/multiply method. Thanks for answering btw :)
You can convert a string into an integer with taking modulo.
Even though the linear sieve has a time complexity of O(n), still, the time taken to iterate through the vector of primes, makes it slower when compared to the classic sieve of eratosthenes. In practice, the classic one with a few modifications like crossing out multiples of 2 in a separate loop and then only dealing with the odd numbers in the "main" loop, is faster.
Proof?
I benchmarked it. You can check it as well.
Link?
I benchmarked locally, no link sorry. You can do and check if you feel skeptical. Time Complexity improvements doesn't always translate to actual execution time improvements.
Can you put the code you wrote in a pastebin or something? It would save a lot of time for others to verify.
I'm not sure if that counts as good benchmarking, but here goes : old vs new seive
Thanks. I slightly changed the old sieve in your code to use i*i instead of i*2. Also made the time measurement more accurate. Also made N = 1e8.
ajkdrag, looks like you were wrong. Linear sieve is almost twice as fast.
https://ideone.com/HMjE7c
And a segmented sieve is even faster: https://ideone.com/d8mlsS
I had Aitken's sieve in my codebase, since I read somewhere that it is very fast. I also benchmarked that implementation, and it turned out really slow. So I decided to play a little bit more, to find a new implementation for my codebase: https://ideone.com/I4piBg. Optimized means, that I skip all even numbers (don't even allocate memory for them, i.e. is_prime[i] checks if i*2+1 is prime).
Here is the pastebin link : https://pastebin.com/exBZdLJK
I checked on Ideone, the time was more for the linear sieve (idk why?)
Don't use Java. The library performance is really bad. Especially for TreeSet/TreeMap.
Actually the "oldsieve" isn't very optimized. I made a better version based on https://codeforces.com/blog/entry/54090?#comment-382736 which has a complexity of O(n*loglog(n)) and now it's pretty much the same. https://ideone.com/NB3fYR
Maybe with n > 1e10 you start seeing some differences but with n = 1e8 it's pretty much the same (sometimes even a little bit faster).
I think that even though we see the modulo operation (%) as O(1) it's actually heavier than that. If you can replace it with some assembly ninja trick you might get faster
This is quite nice, though I have a small issue with calling it the "linear sieve", especially since there is something called the linear sieve from math which is quite different from what is described here (see for example this blog post by Terry Tao. If this technique is actually related to this, I would be very curious how it is the case that this is related to the ideas behind the linear sieve the link discusses.
Just a note, I think your code for calculating the totient function has an edge case where you don't calculate phi(1). I think you need to set phi[1]=1 at the beginning of your loop.
Nisiyama_Suzune you forgot to mention the following things in your blog:
In your functions to compute euler's totient function and the multiplicative function you didn't write phi[i] = 1 and func[i] = 1 respetively.
In both of them you didn't break the loops if
i * prime[j] >= n.You used a further simplification of the formula for f(ip) which you didn't mention i.e.,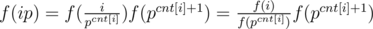 .
.
It'll be helpful for future readers if you can make these changes in the blog.
BTW, a really good blog.
Regarding 3.: This division trick doesn't actually work when f(pk) = 0 for some k > 0. In that case you need the original multiplication. It's probably easiest to keep track of both cnt(i) and pcnt(i) so that the division i / pcnt(i) can be done fast.
Fixed. Thank you!
It's possible to make this much faster by storing the smallest prime factor of each number while sieving (instead of the current bool). That way you can avoid the expensive modulo check in the inner loop and just do
if(primes[j] == spf[i]) break;instead.This gave a ~4x speedup on my machine.
This optimization doesn't work for me. It actually makes the sieve significantly slower. Am I missing something?
See benchmark here: https://ideone.com/z11b4t
For 1e8, I get .34 without that optimization, and .44 with that optimization. I suspect a large reason why is that doing that optimization requires switching your sieve from a boolean to an integer.
Can anyone explain in the linear sieve algorithm "Therefore, if we only loop for all elements in prime in the inner loop, breaking out when the element divides i, we can pick out each composite exactly once." I don't understand why stoppping when prime divides i allows me to pick out each composite once
In this way we visit each composite x = i*prime[j] only when i is the greatest number that divides it (exluding x itself)*. Therefore, since for every number x there is only 1 such number (its greatest divisor exluding x), we will visit each composite exactly once.
*Proof: We will prove that if i = k*prime[j] (i.e. i%prime[j] = 0), then i is not the greatest divisor of x = i*prime[j+1] (excluding x). Well, since x = i*prime[j+1] and i = k*prime[j], we get that x = k*prime[j]*prime[j+1]. Therefore k*prime[j+1] divides x, and k*prime[j+1] > k*prime[j] = i. QED
Example: (I ran the code given for n = 50 and next to each i I wrote all x = i*prime[j] that were visited in the inner loop. Notice that every composite is only visited once) 2: 4| 3: 6 9| 4: 8|
5: 10 15 25| 6: 12| 7: 14 21 35 49| 8: 16| 9: 18 27| 10: 20| 11: 22 33| 12: 24| 13: 26 39| 14: 28| 15: 30 45| 16: 32| 17: 34| 18: 36| 19: 38| 20: 40| 21: 42| 22: 44| 23: 46| 24: 48| 25: ... (for i = 25 to 49, no x were visited)
In the calculation of φ(ip), you wrote φ(ip) = pφ(i) . If I am getting it right , since φ() is multiplicative therefore φ(ip)=φ(i)φ(p) right?? and φ(p) where p is prime and k = 1, we have φ(p) = $$$p^1 — p^{1-1}$$$ equal to p-1 , therefore φ(ip) becomes φ(i).(p-1) . In the code you have also done the same
HELP, Δ F(n) = F(n) - F(n - 1) is multiplicative and Δ F(p^k) = p^k - p^(k - 1) How do we prove these relations in the second problem?
I didn't understand the extension on the linear sieve part: basically, The relation between f(ip) and f(i),f(p). Can someone please elaborate on that