Hi, when we have to do range updates on a segment tree from LEFT to RIGHT with a value VAL, we implement this easily because we have to update every INDEX between LEFT and RIGHT by a constant value VAL. My question is -> If we have to update a segment tree from LEFT to RIGHT with values like k, k+1, k+2, k+3,..... k+(RIGHT-LEFT) on INDICES = LEFT, LEFT+1, LEFT+2, LEFT+3,.... RIGHT respectively where 'k' is a random integer provided in the input. How do we do this type of range updates (efficiently of-course) ? MANY THANKS IN ADVANCE.
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3947 |
| 2 | jiangly | 3734 |
| 3 | Radewoosh | 3646 |
| 4 | jqdai0815 | 3620 |
| 4 | Benq | 3620 |
| 6 | orzdevinwang | 3612 |
| 7 | ecnerwala | 3581 |
| 8 | Geothermal | 3569 |
| 8 | cnnfls_csy | 3569 |
| 10 | ksun48 | 3479 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 162 |
| 2 | maomao90 | 160 |
| 3 | nor | 156 |
| 3 | adamant | 156 |
| 5 | cry | 155 |
| 5 | atcoder_official | 155 |
| 5 | -is-this-fft- | 155 |
| 8 | maroonrk | 153 |
| 9 | SecondThread | 147 |
| 10 | Petr | 146 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Aug/23/2024 22:08:04 (l2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Adding Arithmetic progression to range using Segment Tree
It certainly depends on the update you wish to perform. For that case you mention, you update nodes with an arithmetic progression. I'd do it by maintaining three values for each node, K[i] = first term of progression, D[i] = difference between consecutive terms of progression and S[i] = current sum of node. Then to update the sum for a certain node i of size sz with a progression of first value k and difference d, we would add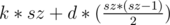 . The update to first terms and differences is a simple addition. We only need to be careful about updating the first term when moving to the right in updates that cover multiple ranges. Lazy updates work in the same way.
. The update to first terms and differences is a simple addition. We only need to be careful about updating the first term when moving to the right in updates that cover multiple ranges. Lazy updates work in the same way.
Consider a problem with two types of queries:
Then this code solves the problem implementing the approach explained above.
Can you just briefly explain how you are updating right and left children ? I didn't understand that part. Thanks !
That's so nice thank you!
Do we need to maintain the arrays
KandDhere?