Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 9 | TheScrasse | 144 |
| Name |
|---|



Pardon me if I am wrong, but can 2C be solved using some sort of a ternary search? Given x slices of type 1, and y slices of type 2, is there an optimal greedy way of distributing them? If yes, I believe ternary search can be applied (I may be wrong, of course). Any help will be appreciated, thank you in advance!
It is not needed, you know the number of pizzas of type A is (sum of pizza slices eaten where A greater than B / slices per pizza) plus or minus one, or the (sum of pizza slices eaten where A greater than or equal to B / slices per pizza) plus or minus one.
Yes, Ternary Search can be applied. The optimal strategy of distributing slices among contestants is same as mentioned in the editorial.
You can see my submission using Ternary Search here.
Although it is not needed as pointed out by farmersrice
So is 865C solved in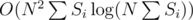 ?
?
Can someone elaborate Div2 E?
Um, this is actually the solution kfoozminus explained to me:
Let's maintain two multisets, "unused" and "already sold". After taking input "x", I tried to sell this pairing with a previous element(which I'm gonna buy). Took the minimum valued element among "unused" + "already sold" stuffs, let's call it "y".
The solution actually comes from the idea — If I see that there's an "already sold" stuff smaller than x, it'd be optimal to sell "x" and not use y, rather than use y and buy x.
Could you explain some details about DIV1-C?
To complete to whole game, or game suffix?
Could you clarify it? Binary search should be made by K or by answer?
And is there a code, which corresponds the idea from editorial?
You assume that the answer is K and compute f(K) (using dynamic programming). The answer is such x that x = f(x). Since f(x) is monotone, binary search can find an answer.
Another view is as follows: assume I tell you that the answer is K. How do you verify that?
Take a look at my submission. Keep in mind that the upper bound is very coarse and the number of iterations in the binary search is unnecessarily large.
Can you please explain the "else" part? I was not able to figure out why it would be S[j]+ans in this case
If i + S[j] > R, it means that when you're unlucky and the current level taking requires the longer timeslot causes you to be over the limit, you have to restart the game after finishing this level.
So in this case isn't play += ans * (1-P[j]) sufficient?
No. You need to spend the S[j] seconds playing, and only after that you can restart. Quoting the statement:
Thanks for clarifying :D
What is the semantics of K and f(K) ?
Did you mean, that the answer is such x that R = f(x)?
And could you clarify about "upper bound coarse"? I thought, that the iterations count difference between upper_bound and binary_search is very low, at most 1-2 iterations.
you calculate the answer using dp, but anytime you start from the beginning you use K instead of dp[starting state] which is not yet calculated.
f(K) is the answer for dp in starting state
Now first thing to understand that if K is answer, then you will get K as answer to your dp (that's easy) Now understand that if K is more then answer you'll get more then answer (because all number can just increase) but less then K (thats harder)
So now function f(k) — k has one zero and you search for it with binary search
How can we show that if K is more than answer, f(K) will never be equal to K?
Got the idea, thanks!
I am confused by the upper bound in this problem. How would the upper bound of the binary search be calculated?
The worst case should be that R is the sum of Fi's, Fi's are 99, Si's are 100 and Pi's are 80. So one has to pass every stage quickly to make it in R seconds. If I am right, how does this lead to the upper bound?
Oh, is that:
Yup, it's around that. But in the contest I just went for somewhat more generous bound. You don't want to fail a task just because of this, and time limit wasn't an issue.
I don't understand why the upper bound of expection is not R but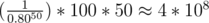 . Can you explain?
. Can you explain?
In the best case, you have to pass all 50 stages fast — any slow move will result in a replay. You pass the whole game in one shot with probability 0.8^50. So, the number of game required for such one shot exists is 1 over 0.8^50. For each such pass you may have to play at worst 50 stages each with no more than 100 units of time. (This is a rough upper bound, so it is not that tight, but also enough for a binary search)
Finally, i've got the idea of the solution, thanks!
Also, i've understood your notice about too big upper bound, it wasn't about std::upper_bound function :)
I still have the only question about optimal progress reset strategy. If I've got you solution right, the optimal strategy is to reset a progress only if all levels completion with slow completion of the current level becomes greater than R. Why it is right?
It doesn't take in account the relation between Fi/Si/Pi at the beginning and at the ending. It seems, that in one situation it could be more profitable to reset a progress after slow completion of the first level, and in another situation it could be profitable to reset progress nearby before final level, but don't see it in DP calculation.
Let's call a strategy a decision in which cells of the dp we will hit restart. Then for a fixed strategy P the function f_P produced by the dp is linear. Now f(x) = min f_P(x). So f in convex upward. Also f(0) > 0. Thus f(x) = x has at most one root.
It is also possible to use Newton's method in problem C to make less iterations. My solution converges in 4 iterations. I believe the Pi ≥ 80 restriction is also unnecessary for this solution. 30890918
EDIT: Missed part of statement.
Can Div1 C be solved without bin search? Let's calculate p[i][t] — probability to finish game in at least R seconds if we are at the i-th level and t seconds have passed. Now, I think, it is optimal to go to the start every time when p[i][t] < p[0][0] (Is this correct?). Now let dp[i][t] be probability that we are at the i-th level with t seconds passed. Let's say answer is S. Then formula for S will be something like this S = dp[n][t1] * t1 + dp[n][t2] * t2 + ... + dp[i1][T1] * (S + T1) + dp[i2][T2] * (S + T2) + ... first we add runs which were successful (completed in less then R seconds) and then we add runs where we either chose to go back or got bad score and had to go back. We do simple dp and accumulate constant values and coefficients of S. In the end S = CONST / (1 - COEF) My code sometimes gives wrong answer, for example third pretest. In my code good[i][t] means probability to finish game with at least R seconds if we are at i-th level and t seconds have passed.
According to me, your statement:
it is optimal to go to the start every time when p[i][t] < p[0][0]is incorrect. We have to minimize the expected amount of time we play.Say dpi, j is the expected amount of time needed to play to finish in less than R seconds such that j seconds have already passed and we are at the ith level. It is optimal to reset if dpi, j + j > dp0, 0. But since we don't know what's dp0, 0, we say dp0, 0 = K for some K and verify if it's possible or not. If it's possible for K, it's possible for all values > K. So, we can apply binary search on K.
Why the following approach is not valid? Let sumA be the sum of all slices of pizzas from the contestants where ai > bi. I sort the participants by (bi-ai), and then i distribute the pizzas starting from the index 0. When i take K slices of a participant that has ai > bi, i make sumA -= K. When i know that sumA < S, (i.e i can't eat more entire pizzas with sumA), i know that i have to share the remainder sumA slices. Submission: http://codeforces.com/contest/867/submission/31151505
can anyone tell how to compute p(x^(-1))mod Q(x) in question G
Hi, I have a question regarding 865B — Ordering Pizza. I've debugged for so many hours that I decided to ask for some insight. I always get runtime error for Test case 5. And I simply have no idea which part of my code, pasted below, could cause run-time error. Any insight is appreciated. Thanks!!!!
Your compare function is incorrect, as comp(a, a) should return false.
Would this logic work in Problem E of Div 2?
Take maximum of 1 to N from segtree and let its index be x . We will sell a stock at this index and take minimum of 1 to x-1 from segtree and let its index be y. We will buy stock at index y. Now remove this values from segment tree. And keep on doing this till all values have been exhausted.
I tried this solution but i am getting wrong answer
submission: http://codeforces.com/contest/867/submission/39457512
Does anyone know how to prove the correctness of the greedy algorithm for problem D (Buy Low Sell High)? Thanks.
Have you found a way to prove the correctness of this problem?