Let's discuss problems. How to solve C,K?
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/27/2024 07:30:48 (k2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










How to solve I?
G, L?
G: You can use dijkstra-like approach: start from vertex n with expected(n)=0. Relaxation will looks like: for vertex V we will use edges corresponding only to fixed(by dijkstra algo) vertexes.
L: you can find answer for squares with/without rotation by 2D scanline (for rotated squares you need to make transition to diagonal coordinate system), and then you need to merge both answers by rotating second. Implementation little bit tricky and unfortunately we didn't have enough time to debug it, but I think that it is correct idea.
We thought about this solution but also didn't write it.
Finally we wrote O(n·1500) solution and it got TL.
I wonder if there exists a bit easier solution.
I solved it with prefix-sums. For rotated squares I just built 4 arrays, for each triangle type that is a half of rectangle cell, and used diagonal-2d prefix sums without explicit rotation. Idk if it is easier, but it uses single coordinate system. https://ideone.com/PXu3Np
Here's an implementation of the in-memory painting algorithm described in the slides. It's surprisingly simple: https://pastebin.com/NxJt4C9k
a[x][y] = k tells us we need to paint the type-A square of size k: (x, y) — (x + k, y + k).
b[x][y] = k tells us we need to paint the type-B square of size k: (x, y) — (x + k, y).
You can figure out the painted area for each unit square (x, y) — (x + 1, y + 1) by looking at the values at a[x][y] and in the neighborhood of b[x][y].
How to solve J?
Let's try every possible k. If we delete k edges there will be k + 1 components, each of size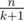 . There are about
. There are about 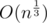 possible k.
possible k.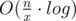 .
.
Now we have another task. Determine if we can split tree into parts, each of some size x. Let's root our tree and calculate pr[v] — nearest vertex on path from v to root, and sz[v] — size of subtree with root = v. Let's notice that if we delete edge (pr[v], v) then x must be a divisor of sz[v]. So let's iterate over all v that satisfy this condition in increasing order of sz[v]. And now when we are in vertex v, we want to know how many edges we have already deleted in subtree with root = v. If we deleted y edges then sz[v] must be equal to (y + 1)·x, then we can delete edge (pr[v], v). It can be done in log(n) with fenwick tree and top-sort.
So for fixed x it works in
My teammate had an interesting simple solution to this problem.
Run DFS from vertex 1 to calculate the number of vertices in each subtree. Then to check if the tree can be divided into components with K vertices in each component:
There is a harder problem which contains the same idea.
Short statement: A tree T1 has a divisor T2 if we can delete some edges from tree T1 so that the remaining trees in the forest are isomorphic to T2. Given a tree find how many divisors it has.
K:
We can consider knobs with single maximal shift (otherwise every shift would be maximal, so we can skip this knob). So we have xr for each 1 ≤ r ≤ n, at each step we can add some value to some segment. Let's do it in another way: add v to yl, add - v to yr + 1. Then calculate prefix sums of y, this new array must be equal to x. From this we can find all values of y: yr = xr - xr - 1.
Now the answer depends only on amount of each value modulo 7. Our operations are: add v to some value, add - v to another value or just add v to some value. The goal is to get all zeros. If we draw an edge between two values iff they were in one operation, then each connected component will have zero sum modulo 7. But each component of values with zero sum can be eliminated in
component_size-1steps. So we want to find maximal number of disjoints components with zero sum. After eliminating all z with - z (modulo 7), we are left with ≤ 3 values, so we can handle them with O(n3) dp.The slides from the solution presentation held onsite may help to get high-level ideas: goo.gl/bwJpds
Some problems have multiple ways to approach them, so keep the discussion going!
I have a question about the solution of I described in the editorial: why we can consider only segments expanded to the right from [mid;mid + 1] and to the left of it? Maybe we must improve the answer by the intersection of the smallest "left" and "right" segments containing the query, but not the smallest of them?
Expandoperation can be implemented as follows:In slow solution we can call
expand(l, r)until we get good interval, call this operationgetAnswer(l, r). Another observation: if l ≤ l' ≤ r' ≤ r, then segmentgetAnswer(l, r)will contain segmentgetAnswer(l', r'). So the answer for[l, r]must contain answers for any l ≤ l' ≤ r' ≤ r.Even more: as far as I understand, answer for[l, r]equal to union of answers for any set of segments with union of this set is exactly[l, r].UPD: the last statement obviously not true, we can take all segments with length = 1; maybe we must make this set of segments connected (edge between segments iff their intersection is not empty). Anyway, this is true for {[l, mid + 1], [mid, r]}.
Yes, I had it wrong in the presentation. Thanks for pointing it out!
I believe it should be:
1) Within the left intervals find the smallest one that covers a.
2) Within the right intervals find the smallest one that covers b.
3) The union of 1) and 2) is the smallest interval that covers the entire [a, b] range.
Our solution of I that passed is as follows: for each i we take values i and i + 1 and find what interval they generate. After this step for each query [x;y] we find min and max on the segment and unite intervals for all .
.
How we do the first step: take minimal segment containing i and i + 1 and start to expand it step by step using sparse table (take min and max on the segment, take min and max on corresponding segment of the inverse permutation and so on). The only hack we use is when i - 1 got into current segment, we relax the borders of the current segment by the interval found for i - 1 and i.
We don't know whether it works on all permutation in less than O(n2) and don't have an idea of counter-test, so I'll appreciate any help in understanding the complexity of this solution :)
Do you look only at (i-1, i), or at each less pair? If only i-1, I think the following test will be counter-test:
1 6 2 3 9 4 5 12 7 8 15 10 11 18 13 14 21 16 17 24...
In this test almost all pairs i and i + 1 that are not consecutive in the array have i - 1 between them, so we relax them fast, don't we?
Pair 5-6 have 4 between them, but there is nothing to relax, because 4 and 5 are near. Same for 8-9, 11-12 etc
Thank you, it works 17s on this test =)
Sorry If this is stupid question. But Can you please mention some details about these contests in blog. I have seen similar "Grand Pix" blogs before as well.. Where can I find problems of these contests?
What is Grand Prix?
This particular round was based on problems from CERC 2017.
Problem A was difficult to implement, used much lines. It was the problem mostly about proper sorting. Later upsolved it more compactly.