You are given the first n (or n + 1 if necessary) terms of a former power series P(x) = c0 + c1x + c2x2 + .... What operations can be performed efficiently?
Obviously, P(x) + Q(x), P(x) - Q(x), P'(x),
 , kP(x) for a given constant k, can be done in O(n).
, kP(x) for a given constant k, can be done in O(n).P(x)Q(x) can be done in O(nlogn) by FFT.
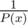 can be done in O(nlogn): Link, check problem E
can be done in O(nlogn): Link, check problem E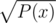 can be done in O(nlogn): Link, check problem E
can be done in O(nlogn): Link, check problem Eexp(P(x)) can be done in O(nlogn): Link, check Figure 1, left
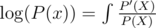 : Link
: LinkOpen: Can we do more complicated operations like P(Q(x)), P(x)1 / k, sin(P(x)), arcsin(P(x)), etc.? Are there other important operations?
Probably a bit related to the computation of
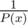 : when we are given two big decimal number x and y, can we compute x / y?
: when we are given two big decimal number x and y, can we compute x / y?











Composition can be computed in time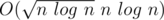 (http://www.eecs.harvard.edu/~htk/publication/1978-jacm-brent-kung.pdf )
(http://www.eecs.harvard.edu/~htk/publication/1978-jacm-brent-kung.pdf )
P(x)α can be computed as exp(α log P(x))
arcsin(P(x)) can be computed in time O(n log2 n) using Newton's method (source : https://hal.archives-ouvertes.fr/AECF/ ).
I have never done this before, but seems to me that
and complex numbers can be implemented as pairs of residues modulo 998244353 or any other good number. Not sure that this will be fast, though.
We don't even need pairs because - 1 is a quadratic residue modulo p (if p if NTT-friendly).
I think calculating P(Q(x)) is not so hard and can be done in this way.
1. Calculate Q(x) for x = 0, 1, 2, 3, ... , 2n. We can use multi-point evaluation and it can be done in O(nlg2 n).
2. Calculate P(x) for x = Q(0), Q(1), Q(2), ..., Q(2n). Since you calculated the value of Q(0), Q(1), ... , Q(2n) in 1., so it can be done by multi-point evaluation of less than or equal to 2n + 1 points so it can be done in O(nlg2 n).
3. So now you have values of P(Q(0)), P(Q(1)), P(Q(2)), ... , P(Q(2n)). You can use interpolation method and you can get Lagrange polynomial in O(nlgn).
So I think overall operation is O(nlg2 n).
UPD: I was wrong, thanks Kaban-5 for pointing out.
Even if P and Q are just polynomials of degree n, you can't find first n terms of P(Q(x)) by interpolating it from values (at least not in any straightforward way), because there is little connection between values and first terms of polynomial.
For example, let n = 3, P(x) = Q(x) = x3, then P(Q(x)) = x9. However, what last interpolation will give you is some polynomial of degree less than 7 that coincides with x9 in points 0, 1, ..., 6, which is obviously not what you expect (because it is not zero, hence, is not prefix of P(Q(x))).
I have seen power, composition and inverse used in problems involving generating functions, but haven't seen examples of using exp, log, sine, arcus sine. Have there been problems / can someone design a problem requiring the calculation of them in context of competitive programming? Maybe some kind of recurrence relation which produces a second order differential equation? I'm not certain how to fix the initial conditions, etc.
See discussion of problem H here: http://codeforces.com/blog/entry/56414
Do you perhaps have a direct link to the problem statements? I'm not a Russian speaker and seem to have some difficulty navigating http://opencup.ru/.
It seems that problems from this season are only accessible by competitors. We have to wait until the season finishes to get the problems statements :(
Thanks for your help!
You can obtain most of functions over formal series using Newton's method.
For example,
(You may see corresponding section here)
Also Lagrange inversion theorem may be useful. For instance in case of equation
You can solve it as
And also
Since $$$\frac{\partial}{\partial x}{\arcsin P}$$$ equals $$$\frac{P'}{\sqrt{1 - P^2}}$$$ rather than $$$\frac{1}{\sqrt{1 - P^2}}$$$, the correct formula is actually as follows:
Do You Mind explaining FFT or Can we provide the source from where can I read the same? Thanks! P.S: I already googled FFT but I didn't understand there,that's why I am asking here. I don't know why all guys are downvoting. If I did something wrong then point me. You guys are demotivating me to ask a question here. I am Feared to ask anything in this community now. Thank you all Guys!!!
$$$[x^n] P(Q^{-1}(x))$$$ where $$$Q^{-1}(x)$$$ is the functional inverse of $$$Q(x)$$$. (We assume $$$Q(x) = ax + O(x^2), a \neq 0$$$.) This can be done in $$$O(n \log n)$$$-time using Lagrange inversion theorem (if the modulus is NTT-friendly).
Detailed explanation is provided in the tutorial of this problem.