Hello Codeforces! Some months ago I wrote tutorial about basics of recurrent sequences. This blog, my second tutorial is about mine another favorite topic — Invariants and Monovariants. These are useful concepts which will help you solving problems, especially, constructive ones. Even if you are not familiar with this topics, I'm sure that you solved problems with use of invariants and monovariants without knowing it, continue reading, you will understand my point :) There will be hard problems which are based on old IMO problems, so I will try my best to explain solutions of examples.
So, what are Invariants and Monovariants? An invariant is a quantity that doesn't change. A monovariant is a quantity that changes monotically (that is, non-decreasing or non-increasing). Seems simple, yes?
Let's start with a few easy examples which you will better understand its point. I suggest you to try solving problems by your own before reading solution. Example 0.1: All numbers from 1 to 100000 are listed in the board. For each number in this board, we replace that number with its sum of digits while resulting number is bigger than 9. At the end, obviously, all numbers will be in range of [1, 9]. Determine which is bigger, number of 1's in new sequence or number of 2's?
Solution 0.1: It is a standard and easy problem, maybe you solved this type of problem before. We will use one well known fact to solve problem — S(n) - n is invariant in modulo 9, it is always 0 (where S(n) donates sum of digits of n). So, resulting number will be old number modulo 9 (if this value is 0, it will be 9). For example, take number 1234, if we do given operation, resulting number will be f(1234) = f(1 + 2 + 3 + 4) = f(10) = f(1) = 1, which is indeed equal to 1234 modulo 9 (let f(n) show given operation). Finally, new sequence will be like this: 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3, 4, 5, 6, 7, 8, 9, ...., 1, 2, 3, 4, 5, 6, 7, 8, 9, 1. You can see that count of 1's here is one greater than count of 2's, finding count of them is easy from this sequence also.
Example 0.2: You are given 20 cards which all numbers from 0 to 9 appears in these cards exactly 2 times. Can you rearrange this cards such that, there will be i cards between cards which i is written on them (that is, cards of 0's will be adjacent, there will be 1 card between cards of 1's and so on).
Solution 0.2: This problem is a little trickier. Let the first position of card of i be ai (position of first card is 1 and last card is 20) (that is, a0 is first position of card of 0, a1 is first position of card of 1 and so on). Therefore, second position of card of i will be ai + i + 1. Sum of ai + (ai + i + 1) would be equal to sum of all numbers from 1 to 20, because there are all positions in union of ai's and ai + i + 1's. That sum is, (a0 + a0 + 0 + 1) + (a1 + a1 + 1 + 1) + ... + (a9 + a9 + 9 + 1) = 2 * (a0 + a1 + ... + a9) + (1 + 2 + ... + 10) = 2 * (a0 + a1 + ... + a9) + 55 = 1 + 2 + ... + 20 = 210. From there, 2 * (a0 + a1 + ... + a9) = 155 which is impossible, since 155 is odd number.
Remark: As you can see from this problem, there is no very special things in invariant. We used being even of 2 * x as invariant. In next example, we will solve harder problem, which it can be used as competitive programming problem.
Example 0.3: There are 2n people (let them be 1, 2, 3, ..., 2n) and some of them are enemy to each other. It is guaranteed that, each of 2n people have at most n - 1 enemies. Initially, they sat on circular table in given order (i is neighbor of i - 1 and i + 1 for 2 ≤ i ≤ 2n - 1 and 1 is neighbor of 2n). Print finite list of moves which will rearrange people such that enemies will not be neighbor, or determine rearranging them is not possible. Here move is printed like: "1 l r" which means reverse places of people in segment [l, r] taken clockwise and "2 l r" which means reverse places of people in segment [l, r] takes counter-clockwise. Here is an sample for understanding problem better: Let n = 2 and enemies are {1, 2}, {3, 4} (that means 1 and 2 are enemy to each other, also 3 and 4 are enemy to each other). Order of sitting is {1, 2, 3, 4} shown as in the picture:
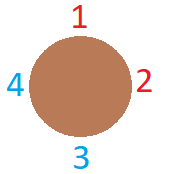
We want to rearrange that positions with moves such that people with same color will not be neighbor. For that, we simply reverse [2, 3] taken clockwise order. New positions will be:
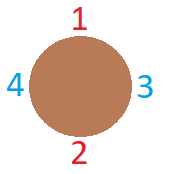
Which satisfies our condition.
Solution 0.3: We will prove that that finite list of moves are always exists. Let A and B be enemies who are neighbor, for simplicity, consider A is on the left side of B (in aspect of B).
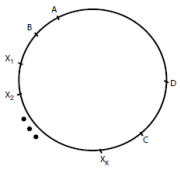
There are at most n - 1 enemy of A, so there will be at least n people who is not enemy of A, let them be C1, C2, ..., Cn. For each 1 ≤ i ≤ n, mark Di as right neighbor if Ci (from aspect of Ci). Enemy count of B is at most n - 1, so all of Di's can't be enemy of B, let D = Dk be one of them. Say that C = Ck and X1, X2, ..., Xt be persons who is sitting between B and C. Now, reverse [B, C] taken counter-clockwise, shown in the picture:

See, nobody expect A, B, C, D changed neighbors. A and C are not enemy, neither are B and D, so number of neighbor enemy pairs decreased at least one and it is our monovariant in this problem. Obviously, after finite moves, count of neighbor enemy pairs will be 0 as wanted in statement.
Remark: Did you see that problem on any judge before? If yes, please write it in comments, otherwise I'm planning to put this problem in SPOJ. Now, we have one more interesting problem, but without solution :) Try to solve it and share your solution with us in the comments.
Example 0.4: Equilateral triangle with side n divided into n2 little equilateral triangles of sides 1 with parallel line to big triangle's sides. For better understanding, see the picture for n = 3:
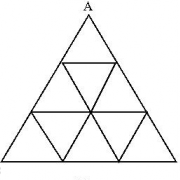
In the given one of the vertices of little triangles, there is written -1, and 1 to all other vertices. For example, we write -1 to point A in the picture, and 1 to all other vertices. Or, we write -1 to point in the middle of picture, and 1 to all others. Check if we can make all numbers 1 with limited number of moves. Here, move is selecting one little triangle and changing signs of numbers on its vertices (that is, -1's will be 1, and 1's will be -1).
Now, we will move to more advanced problems. Next problem is one of the my favorite problems in this topic.
Example 1.1 [Based on IMO shortlist 1989]: A natural number is written in each square of an mxn chessboard. The allowed move is to add an integer k to each of two adjacent numbers in such way that non-negative numbers are obtained (two squares are adjacent if they share a common side). Check if we can make all numbers 0 after finitely many moves (Numbers written on chessboard are given, and we can choose k any number which will not violate given rules).
Solution 1.1: In our problem, it gives us "chessboard" word which is very big hint as chessboard is colored in 2 colors. It could say just board, and it would be harder problem as we would color board in 2 colors (it is called Coloring technique in combinatorics). So, why it is big hint? Let's see. In each move, we are adding the same number to 2 squares, one of which is white and one of which is black. If Sb and Sw denote the sum of numbers on black and white squares, respectively, then Sb - Sw is an invariant, because change of both Sb and Sw is same. Thus if all numbers are 0 at the end, Sb - Sw = 0 at the end and hence Sb - Sw = 0 in the beginning as well. This condition is thus necessary; now we will prove it is also sufficient which will solve problem. Suppose a, b, c are numbers in cells A, B, C respectively, where A, B, C are cells such that A and C are both adjacent to B. If a ≤ b we can add - a to both a and b, making a 0. If a ≥ b, then add a - b to b and c. Then b becomes a, and now we can add - a to both of them, making them 0. Thus we have an algorithm for reducing a positive integer to 0. Apply this in each row, making all but the last 2 entries 0. Now all columns have only zeroes expect the last two. Now apply the algorithm starting from the top of these columns, until only two adjacent non-zero numbers remain. These last numbers must be equal since Sb = Sw. Thus we can reduce them to 0 as well. Also, we can print list of moves with this algorithm.
Example 1.2 [Based on IMO shortlist 1994, C3]: Peter has 3 accounts in a bank, each with an integral number of dollars. He is only allowed to transfer money from one account to another so that the amount of money in the second one is doubled. Check if Peter can transfer all his money into two accounts. If so, print list of transfer.
Solution 1.2: We will prove it is always possible and provide algorithm for transferring money. Let A, B, C with A ≤ B ≤ C be the number of dollars in the account 1, account 2 and account 3 respectively at a particular point of time. If A = 0 initially, we are done so assume A > 0. As we perform any algorithm, the values of A, B and C keep changing. Our aim is to monotonically strictly decrease the value of min(A, B, C). This will ensure that we eventually end up with min(A, B, C) = 0 and we will be done. Now, we know a very simple and useful algorithm that monotonically reduces a number — the Euclidean algorithm. So let B = qA + r with 0 ≤ r < A. Our aim now is reduce the number of dollars in the second account from B to r. Since r < A, we would have reduced min(A, B, C), which was our aim. Now, since the question involves doubling certain numbers, it is a good idea to consider binary representations of numbers. Let q = m0 + 2m1 + …. + 2kmk be the binary representation of q, where mi = 0 or 1. To reduce B to r, in step i of our algorithm, we transfer money to account 1. The transfer is from account 2 if mi - 1 = 1 and from account 3 if mi - 1 = 0. The number of dollars in the first account starts with A and keeps doubling in each step. Thus we end up transferring A(m0 + 2m1 + …. + 2kmk) = Aq dollars from account 2 to account 1, and we are left with B–Aq = r dollars in account 2. We have thus succeeded in reducing min(A, B, C) and so we are done.
I have one more interesting problem, again without solution. It is easier than 1.1 and 1.2, so I believe you can solve it by yourself! Anyway, I added hint in spoiler :)
Example 1.3: Several positive integers are written in a row. Iteratively, Alice chooses two adjacent numbers x and y such that x > y and x is to the left of y, and replaces the pair (x, y) by either (y + 1, x) or (x - 1, x). Prove that she can perform only finitely many such iterations.
Thanks for Kerim.K for providing us following problem and solution with invariant. I let you to solve this problem by your own.
UPD Example 1.4: There are n numbers on the board. In each move, Kerim selects two numbers (let them be a and b) and writes 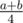 instead of them (that is, he deletes a and b and writes given number). After n - 1 moves, there will remain just one number. If all n numbers were 1 in the beginning, prove that last number will remain after n - 1 moves is greater or equal than 1/n.
instead of them (that is, he deletes a and b and writes given number). After n - 1 moves, there will remain just one number. If all n numbers were 1 in the beginning, prove that last number will remain after n - 1 moves is greater or equal than 1/n.
So, it is end of tutorial. Hope you learned many things from this. If you have and doubts or suggestion, please declare it on comments. Thanks to AoPS for containing IMO shortlists and Pranav A. Sriram for his book "Olympiad Combinatorics".











Thanks for tutorial !
It is on the main page? Really? You guys are amazing!
Hayirli forumlar kardes
BOZKURTLAR ULUSUN TANRI TURKU KORUSUN
Wow, nice tutorial.
sometimes 1 and sometimes 2 numbers vanish, then how do you ensure that 2 numbers remain at the end of the rows?
That two numbers can be 0 also, it doesn't violate our condition.
oh i see, the algorithm works even if some numbers becomes negative at some point as they will become 0 in next step.
Can you please explain the example 0.4. I was not able to understand the problem statement.
Consider n = 2 and you selected -1 as top vertex. All other vertices will be 1. See picture:
Now, you can make moves as stated in problem. For example, if you make move on the first triangle from top (which contains -1), new numbers will be like that:
You need to check if you can make all numbers 1 with such moves.
how to solve example 0.4?? Any hints??
Color the vertices in 3 colors such that no two vertices connected by an edge has the same color. Each triangle will contain vertices of all three colors. Let's consider the parity of number of vertices with - 1 of color 1, 2, 3 respectively. Initially, one of the colors have odd number of - 1 s and the other two colors have even number of - 1 s. Each operation flips the parity for all colors. Thus, in the end, exactly one or two colors have odd number of - 1 s. Thus, it is impossible for all vertices to become 1 s as in this configuration, no color have odd number of - 1 s.
Try this one:
In every move, you select one line and reverse signs of numbers in that line (here line means side of any triangle including big one). Rest of statement is same.
Can you give me a hint for this one?
These are the steps to solve this problem. They do not contain proof.
P.S. I suggest you to try to find "Step 3" by your own after reading 1 and 2.
Prove that -1 can not be on vertices of big triangle.
Find solutions for n = 2 and n = 3.
Prove that it is impossible to make all numbers 1 if n > 3.
Is this the solution for step 3?
Select a 6-vertices hexagon that contain -1, and prove that the parity of the number of -1 in that hexagon will never change.
Exactly :)
Isn't example 0.3 just a variation of Ore's law? Just link non-rivals with edges and you can construct a Hamiltonian cycle from it.
Here is a detailed explanation ->
Ore's Law: If for every two non-adjacent vertexes v, w; deg v + deg w >= n holds, there will exist a hamiltonian cycleFact 1: Using the given operations we can achieve any configuration of the 2*n people.
Now, Make a graph where there is an edge between every two who are friends.
Fact 2: The above graph will have a hamiltonian cycle.
Because of the constraint is given each node deg >= n so for any two non-adjacent v, w; deg v + deg w >= n holds, so the condition for ore's law holds.
Use Fact 1 to obtain the configuration same as the hamiltonian cycle.
How to solve 1.4?
Notice that from Arithmetic Mean — Harmonic Mean inequality we have $$$\displaystyle \frac{a+b}{2} \geq \frac{2}{\frac{1}{a}+\frac{1}{b}}$$$. So, $$$\displaystyle \frac{1}{a} + \frac{1}{b} \geq \frac{4}{a+b}$$$. Therefore, if we change some $$$a$$$ and $$$b$$$ with $$$\displaystyle \frac{a+b}{4}$$$, sum of inverses of the numbers does not increase. Initially, we have $$$n$$$ ones and sum of their inverses is $$$n$$$. If the last standing number is $$$x$$$, then $$$\frac{1}{x} \leq n$$$ and hence $$$x \geq \frac{1}{n}$$$.
This problem can be solved by maintaining an invariant as explained here.