Atcoder Petrozavodsk Contest was held last Sunday, and I found 'problem I' really interesting. Let me share this problem and the way to get to the answer.
This is written in Japanese too: http://www.learning-algorithms.com/entry/2018/02/05/160601
Problem: https://beta.atcoder.jp/contests/apc001/tasks/apc001_i
Summary: There's an H × W grid, and n squares of the grids are colored black, while the others white. Find the sum of the minimum distances of all the pairs of white squares. The distance here, is defined as the minimum steps by which you can move to the left, right, up, or down direction, and can't move to the black square. H, W ≤ 1000000, n ≤ 30
If you have possibly, possibly, read my article on Hirschberg's Algorithm, this problem is not super difficult for you. A close idea is actually used.
http://codeforces.com/blog/entry/57512
First of all, let me vertically divide the grid into two grids, and consider the minimum distance between the two white squares, one of which is in the left grid, while the other is in the right grid. If the 2 columns nearest to the division are all colored white, given that this path is the minimum path, there must be a position which the path goes through exactly once. This means that you can calculate the number of times that all the paths which go through this division, independently, and then contract the 2 columns into 1 column. The value is the product of the numbers of white squares in each grid.
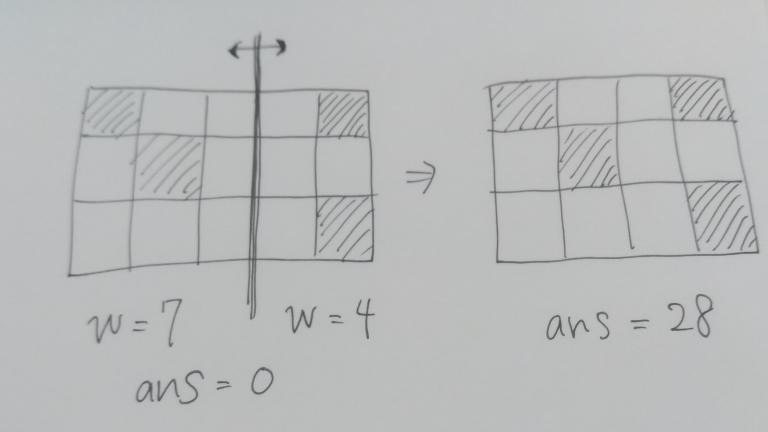
You can make the grid smaller and smaller by repeating this process, and thanks to the restriction, n ≤ 30, the grid is going to be very small O(n) × O(n) grid.
Now, you can do simple BFS in this new grid, but wait, you need to check the weight of each grid.
Suppose you contract the following grid:
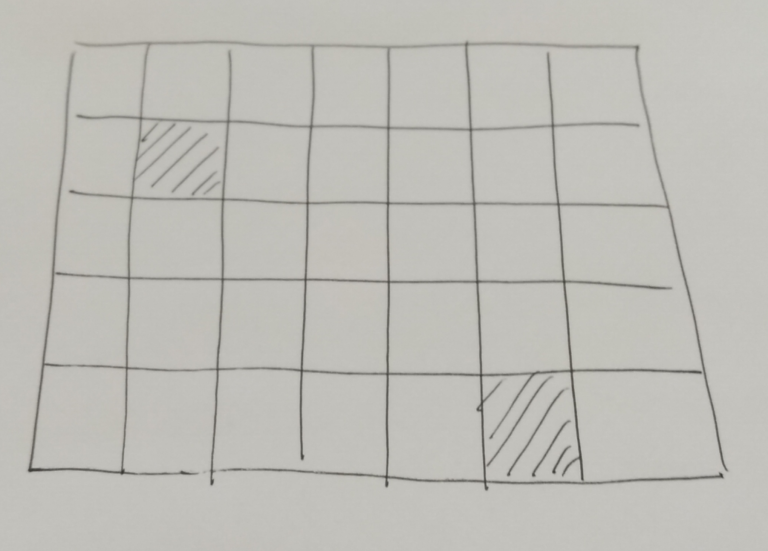
Of course you need to check how many squares are actually hidden in each grid! Thus, the weight of each grid is going to be like this:
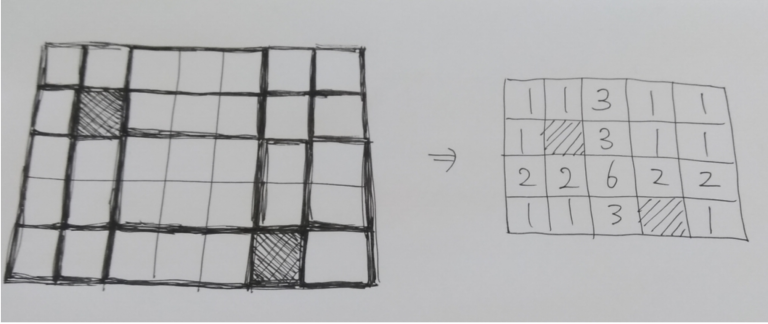
This is easily calculated by seeing columns and rows independently.
On the contracted grid, the minimum distance d between a white square A(weight WA) and another white square B(weight WB) is, the minimum distance between all the squares included in A and all the squares included in B, before the contraction, therefore, you need to calculate the sum of d * WA * WB for all the pairs in the contracted grid. This works effectively enough, in O(n4). If you counted all the paths twice, be careful not to forget to halve the value. Finally, the sum of this value and the pre-calculated value is the answer to this problem.
#include <cstdio>
#include <vector>
#include <algorithm>
#include <functional>
#include <map>
#include <set>
#include <string>
#include <iostream>
#include <cassert>
#include <cmath>
#include <queue>
using namespace std;
const int MOD = 1e9 + 7;
struct state { int y, x, step; };
static const int dx[] = {1, 0, -1, 0}, dy[] = {0, 1, 0, -1};
int main() {
long long h, w;
scanf("%lld %lld", &h, &w);
int n;
scanf("%d", &n);
vector<int> w_cnt(w, 0), h_cnt(h, 0);
vector<bool> w_exist(w, false), h_exist(h, false);
vector<pair<int, int>> black;
for (int i = 0; i < n; i ++) {
int y, x;
scanf("%d %d", &y, &x);
w_cnt[x] ++;
h_cnt[y] ++;
w_exist[x] = true;
h_exist[y] = true;
black.emplace_back(x, y);
}
for (int i = 1; i < w; i ++) w_cnt[i] += w_cnt[i - 1];
for (int i = 1; i < h; i ++) h_cnt[i] += h_cnt[i - 1];
long long ans = 0;
//precalc
for (int i = 0; i < w - 1; i ++) {
if (!w_exist[i] && !w_exist[i + 1]) {
long long left = (long long) (i + 1) * h % MOD - w_cnt[i];
long long right = (long long) (w - (i + 1)) * h % MOD - (n - w_cnt[i]);
ans += left * right;
ans %= MOD;
}
}
for (int i = 0; i < h - 1; i ++) {
if (!h_exist[i] && !h_exist[i + 1]) {
long long left = (long long) (i + 1) * w % MOD - h_cnt[i];
long long right = (long long) (h - (i + 1)) * w % MOD - (n - h_cnt[i]);
ans += left * right;
ans %= MOD;
}
}
//compress
map<int, int> newx, newy;
vector<pair<long long, bool>> widths, heights; //(length, is_white)
{
int cnt = 0;
for (int i = 0; i < w; i ++) {
if (!w_exist[i]) {
cnt ++;
} else {
if (cnt) {
widths.emplace_back(cnt, true);
cnt = 0;
}
newx[i] = (int) widths.size();
widths.emplace_back(1, false);
}
}
if (cnt) widths.emplace_back(cnt, true);
}
{
int cnt = 0;
for (int i = 0; i < h; i ++) {
if (!h_exist[i]) {
cnt ++;
} else {
if (cnt) {
heights.emplace_back(cnt, true);
cnt = 0;
}
newy[i] = (int) heights.size();
heights.emplace_back(1, false);
}
}
if (cnt) heights.emplace_back(cnt, true);
}
//re-write the grid
int neww = (int) widths.size();
int newh = (int) heights.size();
vector<vector<long long>> s(newh, vector<long long> (neww, 1)); //-1 when it's black, weight when it's white
for (auto b : black) {
s[newy[b.second]][newx[b.first]] = -1;
}
for (int i = 0; i < newh; i ++) {
for (int j = 0; j < neww; j ++) {
if (heights[i].second || widths[j].second) {
s[i][j] = heights[i].first * widths[j].first % MOD;
}
}
}
for (int i = 0; i < newh; i ++) {
for (int j = 0; j < neww; j ++) {
cerr << s[i][j] << ' ';
}
cerr << endl;
}
//BFS
long long sum = 0;
for (int sy = 0; sy < newh; sy ++) {
for (int sx = 0; sx < neww; sx ++) {
if (s[sy][sx] == -1) continue;
long long res = s[sy][sx];
vector<vector<bool>> used(newh, vector<bool>(neww, false));
queue<state> q;
q.push({sy, sx, 0});
used[sy][sx] = true;
while (!q.empty()) {
state p = q.front(); q.pop();
if (p.y != sy || p.x != sx) {
assert(s[p.y][p.x] != -1);
sum += (long long) p.step * res % MOD * s[p.y][p.x] % MOD;
sum %= MOD;
}
for (int d = 0; d < 4; d ++) {
int xx = p.x + dx[d], yy = p.y + dy[d];
if (xx < 0 || xx >= neww || yy < 0 || yy >= newh) continue;
if (used[yy][xx] || s[yy][xx] == -1) continue;
used[yy][xx] = true;
q.push({yy, xx, p.step + 1});
}
}
}
}
sum *= (MOD + 1) / 2;
sum %= MOD;
ans += sum;
ans %= MOD;
printf("%lld\n", ans);
return 0;
}










