otero1991's blog

Geometric Sequence!!
By otero1991, 11 years ago, In English

After removing some elements from a geometric sequence (with not necessary integer ratio), I wonder how can I recover this ratio, and if there are some possibles ratios the one with the greatest absolute value. The solution should be linear or nlogn. The numbers are not greater than 10^18

This problem is from the contest Waterloo Local Contest 24 September (Gym)

  • Vote: I like it
  • +5
  • Vote: I do not like it

»
11 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Hint 1: the ratio must always be rational and greater than one by absolute value.
Hint 2: we can have a long geometric series if and only if the ratio is 1 or -1.

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I have been trying with something like a root of the shortest ratio between consecutive elements but still nothing. I will appreciate if you post any solution!! Thanks

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      Let's see the case when our numbers are positive and are sorted in ascending order. In this case the answer would be some root from the ratio between two consequitive numbers. So, we can check an answer just by checking if all of ratios of consequitive numbers are powers of it.

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        But what would be the order of that algorithm?? How can I get the roots from a rational number (the ratio between two consequitive numbers) efficiently. UPD: There are 10^5 numbers

        → Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I can't understand what you mean with Hint 2

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I mean that a quadratic algorithm will be also feasible.

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Still not understanding!!! Please be more specific or if it is possible post your solution!! Thanks!!

        → Reply
        • »
          »
          »
          »
          »
          11 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Let's assume that our answer is p/q, where p and q are integers, q>0 and gcd(p,q)=1. If p/q=1 or p/q=-1, then all the elements must be equal by absolute value and we can easily check it for O(N). Now, let {a_0, a_1,...,a_k} be our geometric sequence, where all elements are integers and their absolute values are not more than 10^18. Then, a_k=a_0*p^k/q^k. If q=1, then abs(p)>=2. Let's notice that if k>=60, then abs(p^k)>10^18 and abs(a_k)>10^18, so this sequence is not valid. Now, if q>=2, then a_k should be a multiple of q^k. But if k>=60, abs(q^k)>10^18 and abs(a_k)>=abs(q^k)>10^18, so this sequence is not valid too. Thus, if not all the elements are equal by absolute value, N can be at most 60, and even O(N^4) solution will be OK...

          → Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Does anyone has another idea???

→ Reply
»
11 years ago, # |
← Rev. 2   Vote: I like it +8 Vote: I do not like it

I think there is something wrong with this problem. because we know that every geometric sequence is donated by two numbers r and a0, where r is the ratio and a0 is the first element of the sequence.

because the input is a geometric sequence after removing some elements. we don't have any way to know what is the first element.

but I will tell you a way to tell the ratio of the geometric sequence assuming that the ratio is guaranteed bigger than 1 and it is exist.

let the elements of the geometric sequence be: a0 , a0*r , a0*r^2 , a0*r^3 , .... , a0*r^k

now after removing some elements the array will become:

a0*r^i , a0*r^j , a0*r^k , a0*r^l , a0*r^m ..... where i < j < k < l < m (assume the number of remaining elements is N)

Let's divide each two adjacent numbers in the array so we get rid of the a0's in the elements so we will have:

r^(j-i) , r^(k-j) , r^(l-k) , r^(m-l) notice the number of elements of the new array is N-1)

now just compute the GCD of the powers of the elements of the new array and you will get the greatest possible ratio of the geometric sequence.

for example the solution is: r^GCD(j-i,k-j,l-k,m-l)

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think that's not correct, since we need to know the largest number that is the base of the noted powers, not the largest that divides all the powers.

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I didn't get you.

      Can you give me an example to show me that my idea is wrong?

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        For example, we are given numbers 1, 4, 32. The new array of ratios is then 4 and 8. We have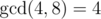 , but the answer to the problem is 2.

        Your approach would work with arithmetic sequence though.

        → Reply
        • »
          »
          »
          »
          »
          11 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          OK, you are right.

          thank you for showing me my fault.

          I've edited my solution, you may read it again.

          → Reply
        • »
          »
          »
          »
          »
          11 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Do you have any other approach?? Remember that ratio could be rational

          → Reply
»
11 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

This is the solution, it works only if it's guaranteed that ratio is integer ,ratio is exist ,the ratio bigger than 1 and 3<=N<=100,000:

#include <iostream>
using namespace std;
int arr[100005];
int n;
int sol;
int GCD_of_power(int a,int b){
	int t,y;
	if(a>b){
		t=a;
		y=b;
	} else {
		t=b;
		y=a;
	}
	if(y==1){
		return t;
	}
	return GCD_of_power(y,t/y);
}
int main(){
	int a,b;
	cin>>n;
	cin>>a;
	for(int i=0;i<n-1;i++){
		cin>>b;
		arr[i]=b/a;
		a=b;
	}
	sol=GCD_of_power(arr[0],arr[1]);
	for(int i=2;i<n-1;i++){
		sol=GCD_of_power(sol,arr[i]);
	}
	cout<<sol<<endl;
}
→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

http://pastie.org/10969065#7

→ Reply