We can adopt an array to store the segment of each file. Each element is in fact a “pair” which contains two values. The first one is the index of the file while the second one is the index of the segment in the current file. Then, the problem is reduced to sorting the originally given array in an imcreasing order with all the empty cells appending at the end.
For an element at position i, we should move it to the target position j. In order to do this, we should move the element at position j to an empty cell and then move that element from position i to j (if i = j, nothing is done). One can see that we implement at most two operations for each element, and thus the total number of operations will not exceed 2(n - 1).
Let us investigate some characteristics of each type. For convenience, we write an integer as t = ambm + am - 1bm - 1 + ...a0b0, where b is the base. Note that it is sufficient to focus on r = b%d instead of b, since we have b = kd + r, and thus bm = qd + rm. One can see that t = q'd + amrm + am - 1rm - 1 + ...a0r0, and the first term does not affect the result. Therefore, we focus on t = amrm + am - 1rm - 1 + ...a0r0 for the following arguments.
2-type: Suppose that it is enough to check the last m terms. This means that for rm, rm + 1, rm + 2, ..., every term must be divisible by d. Note that if rm is divisible by d, then any rm + δ is also divisible by d, and thus it is sufficient to check whether rm has a divisor equal to d. In general, we find all the prime divisors of r and d, respectively. There exists some rm that has d as its divisor if and only if r has all the prime divisors that d has. Suppose that both r and d have a common prime divisor p. More specifically, the quantity of p included in r is a while in d is b. For instance, 12 has two 2s while 48 has four 2s. To find a minimum m, we should guarantee that for every prime divisor, we have a × m ≥ b. For instance, 12 = 22 × 3 and 48 = 24 × 3. For prime divisor 2, we need 2 × 2 ≥ 4 while for prime divisor 3, we need 1 × 1 ≥ 1, and thus we need m = 2, i.e., 122 is divisible by 48.
3-type: Suppose that s = am + am - 1 + ... + a0 is divisible by d. Then, t - s is also divisible by d. Note that t - s = am(rm - 1) + am - 1(rm - 1 - 1) + ... + a1(r - 1), and as rm - 1 = (r - 1)(rm - 1 + rm - 2 + ... + 1) = q(r - 1). Thus, t - s = Q(r - 1), and to guarantee that this is divisible by d, we need r - 1 = 0, i.e., r = 1.
11-type: The idea is similar to 3-type. Suppose that t = a1 - a0 + a3 - a2 + ... + a2m + 1 - a2m, and we have 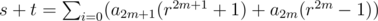 . Note that r2m + 1 + 1 = (r + 1)(r2m + r2m - 1 + ... + 1) = q(r + 1), and similarly r2m - 1 = p(r + 1). Thus, s + t can be written as s + t = Q(r + 1), which implies that r + 1 must be some multiple of d. As we have assumed that r < d, this in fact means r + 1 = d.
. Note that r2m + 1 + 1 = (r + 1)(r2m + r2m - 1 + ... + 1) = q(r + 1), and similarly r2m - 1 = p(r + 1). Thus, s + t can be written as s + t = Q(r + 1), which implies that r + 1 must be some multiple of d. As we have assumed that r < d, this in fact means r + 1 = d.
6-type: We can write d = p × q, where gcd(p, q) = 1 (gcd is short for greatest common divisor). If both (b, p) and (b, q) correspond to a “non 7-type”, then the current (b, d) is a 6-type.
Be careful that r might be equal to zero, and for this case, it is a 2-type and we only need the last digit. Besides, when d = 2, both r = 1 and r + 1 = d hold at the same time, and as the problem required, we should assign it with 3-type rather than 11-type. We can calculate answers for all the pairs of (b, d) previously, and output the answer corresponding to the query.
We use p[i] to denote the number of upper case letters with indices (1, 2, ..., i) (prefix idea). Then, we enumerate the border position which seperates the last upper case letter and the first lower case letter, and calculate the number of modification that we need implement. This number can be computed with O(1) by using p[i].
We denote the first and second string as s and t, respectively. To find a minimum s satisfying s > t, we need find a maximum index i so that s[i] > t[i] while s[j] = t[j] for j < i, and for j > i, we should output the remained letters in s in the order of “a,b,c,...,z”.
We need prefix idea again, for instance, pt[i][26 + 1] to denote the total number of letters “a,b,c,...,z” appearing in positions j, where j ≤ i. Here we use 26 + 1 rather than 26, and “a” is mapped to 1 rather than 0. The reason is that string t may have shorter length than s, and to correctly handle this case, we should append letters that are “mapped to” 0 to the end of t (one can check the comparison rule mentioned in the problem statement, which is associated with different string length).
Therefore, we can enumerate indices from right to left and for each position i, we check whether we can put a letter with value t[i] + 1 at index i while all the letters with indices j < i are exactly the same as t[j]. This can be done with complexity O(26) by using pt[i][26 + 1]. After we find a feasible position, we output the same letters as t before this index and output t[i] + 1 at index i while output the “unused” letters in the order of “a,b,c,...,z”.
We compute for each color the maximum number that can be achieved.
For each color, we find all the consecutive intervals [l, r] (or referred to as segments), and store the left and right borders as a pair, in an increasing order of l. Then, this problem can be solved by using “two pointers” technique, i.e., we adopt two pointers h1 and h2 that point to the leftmost segment and the rightmost segment, respectively, and we are going to combine these segments together. The reasons are as shown follows.
Suppose that the optimal answer for this color is obtained by combining the i, i + 1, ..., j-th segment together. Then, this answer can also be obtained by setting h1 = i and h2 = j, since we will always cover this range as long as it is a reasonable range.
Therefore, we move h1 and h2 as what is usually used in two pointers technique, and compute the answer.
180F - Mathematical Analysis Rocks!
Let us focus on position i. For the first time, it is i. For the second time, it is p[i]. For the third time, it is p[p[i]], and the fourth time it becomes p[p[p[i]]]. As a[i] = p[p[i]], and b[i] = p[p[p[i]]], we have b[i] = p[a[i]], i.e., p[a[i]] = b[i], and thus we can obtain p[i].









