Hi
I frequently think of problems on my own, and try to solve them.
But this simple problem got me dazzled!
Problem Description:
You have a set A, size N, Ai upto 109.
You play N - 1 steps on it.
Each step, pick any 2 elements x, y and remove both of them. Add back abs(x - y) to A.
Print the max value possible at end.
I was thinking that DP might solve this, but I was wrong about the approach that was coming to my mind.
My Approach:
The ans can't be greater than max element, say M.
So find out the minimum possible value that you can have from the remaining N - 1 elements.
A simple DP can be used for this, but this approach is wrong :)
Can anyone solve this?
Happy Coding!











If you can find that minimum value for n-1 numbers, then if it's less than a[n]-a[n-1] you found the answer. Otherwise you should continue your way considering the answer would be less than or equal to a[n-1].
I don't know how you find that minimum value, but I didn't found any counter example for this :
The minimum value we can make is equal to the minimum non-negative number we can make by placing -/+ behind the array's elements.
If this is right (And I'm sure it isn't) then total complexity would be O(n^3*max(a[i])) that is not even good.
Observation: If we start with A1, A2, ...AN, and end with V, then V ≡ A1 + A2 + ... + AN(mod2) (because |x - y| ≡ x - y ≡ x + y(mod2))
Conjecture: if N is big enough, and Ai are bound by some constant value (here: 109), then we somehow(?) should be able to get final value V = (A1 + A2 + ... + AN)%2.Assume A1 ≤ A2 ≤ ... ≤ AN. Now, use this conjecture on A1, A2, ...AN - 1 to get either 0 or 1, and in the end, get AN or AN - 1UPD this conjecture is wrong, for example N is odd, Ai = 2
Man I scratched my head for around a week on this problem, and as soon as I got excited with some new approach, it failed miserably. I was expecting some answer from CF community though, but let's wait a bit more.
If you can use a simple DP to find minimum value then we're done.
let MX = max(Ai) and erase it from the set
for the N - 1 remaining elements repeat this N - 2 times :
let X = max(Ai) and erase it from the set
let Y = max(Ai) and erase it from the set
add to the set the value abs(X - Y)
the remaining element in the set will be MN
Answer = abs(MX - MN)
is this greedy approach wrong ??
1 1 100 You'll get 1-1=0, 100-0=100.
it's easy to get 98
I think he was explaining the solution to find maximum value, and it's 100 in your example.
ah, sorry, right, i thought we need minimum
from problem description :
" Print the max value possible at end. "
Countertest
3 3 4 5 5 6. Your greedy gets 4 while it is possible to get 6.After taking 5 4 we have
1 3 3 5 6. Then take 1 3 and 3 5 and its obvious how to get 6 from2 2 6If you happen to solve it in time O(POLY(n)·POLYLOG(max Ai)), don't forget to claim your million dollars. It is fascinating and frustrating how many different variations of problems we are able to solve in the context of a rather short contest, yet some of them end up NP-hard. This one is the case.
Why is that? We've already established that ans ≤ M, where M is the maximum element. To decide whether answer is M is NP-complete. It is easy to see why this is in NP, so lets concentrate on the reduction from 2-PARTITION.
The answer is M if and only if we can obtain zero from the set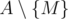 . The operation above can be summed as putting a plus or minus before each element and summing them. We cannot do arbitrary assignment, but we will see that that is not a problem.
. The operation above can be summed as putting a plus or minus before each element and summing them. We cannot do arbitrary assignment, but we will see that that is not a problem.
First see that if the answer is M then we can build a two-partition out of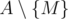 . This is evident, one set would be the elements with '+' in front and the second is the minuses.
. This is evident, one set would be the elements with '+' in front and the second is the minuses.
Let's now assume that an answer to a two partition exists and prove that the answer to our problem is M. To see this, take the two partition and name the (multi)sets B and C. We maintain the sets in such a way that their sum is the equal. As soon as the said sum is zero, we are done -- as it may not contain negative elements, we just sum all the remaining zeros, and then subtract the zero from M. If the sum is non-zero, pick two non-zero elements from each: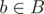 and
and 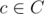 . If b ≥ c, put abs(b - c) into B, otherwise into C. The equality of the sums is preserved. We can see that this process finishes in linear number of steps with a single zero.
. If b ≥ c, put abs(b - c) into B, otherwise into C. The equality of the sums is preserved. We can see that this process finishes in linear number of steps with a single zero.
To summarise, you have an instance P of the decision problem 2-PARTITION. You take the maximum element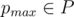 . Solving
. Solving 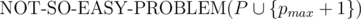 answers
answers 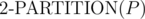 .
.
EDIT: It seems that the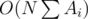 pseudo-polynomial algorithm for optimisation version of 2-PARTITION is able to solve the problem. I doubt that you can do any better.
pseudo-polynomial algorithm for optimisation version of 2-PARTITION is able to solve the problem. I doubt that you can do any better.