No threads, so I decided to make it.
Let's discuss!
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
| Name |
|---|



Hard contest for our team.
What could be a reason for getting WA 44 on problem A?
Overflow? You may need int128.
Could you plase tell how to use int128? I can only do it with boost, otherwise sizeof(int128) shows 16 with g++/clang.
I tested in my environment just now and sizeof(int128) showed 16. However, it seems operations with int128 are working for magical reasons. Looks quite strange.
16 bytes = 128 bits, what's wrong?
True, thanks :D I somehow multiplied by 4 instead of 8 :/
how to solve F and G?
G:
tl;dr, compute how many 0 ≤ i < n, 0 ≤ j < m with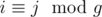 or
or 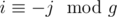 where g is gcd of 2(n - 1) and 2(m - 1) using inclusion-exclusion principle.
where g is gcd of 2(n - 1) and 2(m - 1) using inclusion-exclusion principle.
First, let's get rid of grids and consider the point setting: a ray of direction (1, 1) shoots from the origin and reflects when hitting the boundary of [0, n - 1] × [0, m - 1] rectangle.
For a point (i, j) in the rectangle, it is passed by the ray if and only if there are integers a, b satisfying one of the four conditions: ± i + 2a(n - 1) = ± j + 2b(m - 1). This condition comes from that we can pave rectangles all over the plane and ignore ray reflection.
Above condition is equivalent to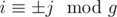 . Then by some elementary math skill and inclusion-exclusion principle we can calculate how many (i, j) satisfying the equation and get the answer.
. Then by some elementary math skill and inclusion-exclusion principle we can calculate how many (i, j) satisfying the equation and get the answer.
There's a 1 line formula... Let me see if I can remember it. Let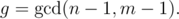 Then the answer is
Then the answer is
You can find this by computing the number of times the bishop goes up and down the board (say $m < n$). This is going to be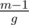 because the smallest integer k such that m - 1|k(n - 1) is
because the smallest integer k such that m - 1|k(n - 1) is 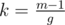 . After that you count number of repeated squares, noting that a square can only be repeated twice or else you get a cycle.
. After that you count number of repeated squares, noting that a square can only be repeated twice or else you get a cycle.
Got presentation error on TC#38... Any ideas of getting such a verdict?
But I believe in my solution: 1) find how many times bishop needs to make a trip from one shortest side to opposite shortest side (it is:
(min(N-1,M-1)) / gcd(N-1,M-1)), then multiply this count by length of this way (which is:max(N,M)), 2) subtract a number of intersections of ways, which is in a grid in a rectangle of( max(N-1,M-1) + 1 )x( min(N-1,M-1) - 1 ), and a number of intersections is( max(N-1,M-1) / gcd(N-1,M-1) + 1 )x( min(N-1,M-1) / gcd(N-1,M-1) - 1 )/2.Can we solve A without fighting with TL? log2 per query is not very easy to pass.
We used N^2 dp for N <= 500 and logn * C (C <= 10, maybe smaller) otherwise, which passes pretty easily, although it's more boring to code
Can you elaborate on how you calculated the k-th binomial of n choose c in O(log2)? We only managed to solve it by doing c binary searches (with increasing and decreasing step size), computing binomials at each step (O(log3) total).
Oh you are right, it was C^2lgN indeed.
Actually we had three cases : One for N <= 500, Other one for N <= 1000000, and N > 1000000. Second case is implemented with DP (as we know C < 10), so it’s ClgN per query.
After the contest, we thought second case was overkill. But now I think we might got TL otherwise.
Precalculate binomial coefficients bin[100][100] one time.
For problem D, we do dynamic programming on the state dp[odd][even][p], where odd, even is the number of connected components of odd/even size, p is the parity of the edges inside connected components that hasn't been added.
UPD: turns out to be a silly bug, the above dynamic programming should be correct.
How to solve I?
Process intervals using a recursive function, starting with intervals containing a single 1, and discarding all intervals with duplicate elements. You can check if an interval of size s is a permutation by checking if its maximal element is s. After checking that, also process the two intervals obtained by extending the interval to the left or to the right to include its mex (smallest missing element).
Let's find all intervals [L, R] such that
Try all N possibilities for R. For a fixed R, find the maximum i such that i ≤ R and ai = 1. Clearly, K is the maximum of ai, ..., aR. Now we can uniquely determine L because L = R - K + 1. Use hashes to check if aL, ..., aR is a valid permutation.
It also proves that there are at most 3N good intervals.
I guess, we have to perform this operation in both directions. If not, how do we find permutations starting from 7, 6 and 5 for input array
7 6 5 1 2 3 4using this algorithm?Thanks. We also thought to make this "search" but didn't notice that there are not much good intervals.
Any proof for I(that answer can't be bigger that 2*n)?
how to solve C?
Just binary search over the coordinate of the line. Once you've fixed it, the problem becomes: find the convex hull and calculate its area. BTW, how to solve D?
No binary search is needed. Just build convex hull iteratively (add points one by one) as a normal algorithm, but keep current area value as well. We compute that for each prefix and suffix so then we get an answer.
Is building convex hull iteratively easy? Isn't this significantly nastier to code than a binary search (whereas normal convex hull is just copy / paste).
I think he meant Andrew’s monotone chain. If you sort by pair of xcoord and ycoord, then this is a simple for loop just like normal convex hull, so not significantly nasty.
Sorry, had to mentioned that. Convex hull with Graham-Andrew algorithm and sum of areas under every segment on top of that.
Why i couldn't enter the contest?
How to solve F?
Assuming dpmask is the number of placing elements from n - k + 1 to n, where k is equal to the number of 1's in the mask and 1's in the mask correspond to the occupied places by numbers from n - k + 1 to n, such that after performing m given operations of swapping these elements will be in their positions (it means that n will stand at n-th position, ..., n - k + 1 will stand at (n - k + 1)-th position after performing all swappings).
dp0 = 1.
Then let's iterate over 0's bits in the mask and try to put there the value n - k (k is the number of 1's in the mask). It means we are processing (adding) elements from n to 1. Now we can check whether it's a correct mask or not. We know that the elements that are 1's in the mask are greater than n - k, and the elements that are 0's in the mask are less than n - k. Now we can construct sequence using number 0, 1, 2, where 0's stand on the positions, that are zero in the mask, 1 stands where we want to put n - k in the mask and 2's stand on the positions, where 1's in the mask. So we just sort this sequence applying given comparisons and if it's sorted in the end, we can do this transition.
Did anybody have problems with test 6 in D? Any ideas what test is it?
We failed test 6 when we missed some initialization.
No idea what the test is, though it should be a fairly simple test, IMO.
K?
First, pick a lexicographically minimal length-k substring, and remove all strings which have such as substring.
After that, you can append other length-k substring, possibly overlapping some. You should try to pick and append the substring to make it lexicographically minimal. (Note that length matters — in case of aabbbcc and aabbbccd, you should pick the former one, as it contains the latter one) After that, remove all strings which have such as substring.
The limit is kinda small, but you should pick a reasonably fast DS or efficient code. I used std::set to maintain the strings.
But what about test:
I mean you choose substring 'a', then 'd' and we will obtain the answer 'ad', but we can delete 'a' from this answer and it still satisfies the statement about lying in each given string, but here is a contradiction with the second condition from the statement.
The answer is "ad", what's the problem?
I got the wrong idea of the second condition, sorry.