bobr_babizon posted an article, a machine translation of a Kinetic Segment Tree post in my Korean blog. Given this interest in my small Korean blog, I felt obliged to introduce it.
In most of my undergrad period, I was sponsored by the generous Samsung Software Membership, where one of their remarkable features was to fund "individual research projects" — In short, each month, I write an article on interesting stuff, and they will pay me 500,000 KRW per article. Amazing, as it motivates me to learn new stuff and also get paid.
Here is the full list of posts written by that initiative.
Not all posts are good. Sometimes, I need to keep up with the deadline and rush the post; sometimes, I write stuff in specific interest; sometimes, the topic is too hard and I only obtain a superficial understanding. But there are some posts, which I think are the best posts on their subject matter for CF audience if translated into English:
- Nine ways to optimize dynamic programming (1/4, 2/4, 3/4, 4/4)
- Push-Relabel Algorithm (1/2, 2/2)
- Solving CP problems on tree decompositions
- Segment Tree Beats and Kinetic Segment Tree
- Introduction to APSP Conjecture and BMM Conjecture
- Solutions to some recent IOI problems (for which there were no published editorials)
Sometimes I actually posted them in English:
- Story about edge coloring of graph
- On Range LIS Queries (1/2, 2/2)
Why are all these posts in Korean? It's because the sponsor wanted such a way — otherwise, I'd actually write all of them in English. So that's pretty sad, and I don't think I will ever try to translate them, but I hope someone would still find them helpful.










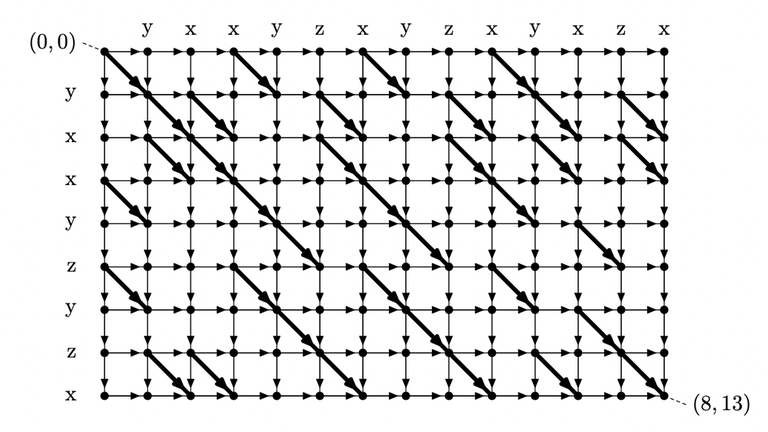
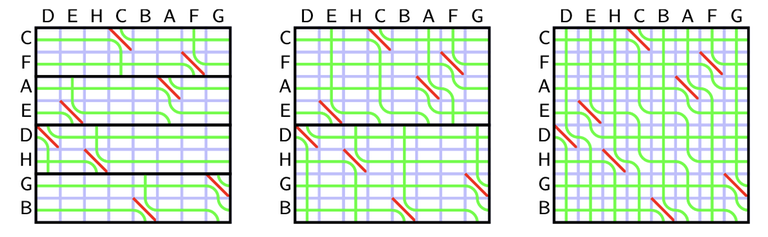 Recall the rules of seaweed: If two seaweeds never met before, then they cross. From this rule, we can easily find the destination for missing columns: The seaweeds will just go downward. Therefore, the permutation for $$$A_{lo}$$$ and $$$A_{hi}$$$ can both be scaled to a larger one by filling the missing columns and missing rows (which are just identity). Then we can simply return the unit-Monge multiplication of them.
Recall the rules of seaweed: If two seaweeds never met before, then they cross. From this rule, we can easily find the destination for missing columns: The seaweeds will just go downward. Therefore, the permutation for $$$A_{lo}$$$ and $$$A_{hi}$$$ can both be scaled to a larger one by filling the missing columns and missing rows (which are just identity). Then we can simply return the unit-Monge multiplication of them.