ko_osaga's blog

Opencup 2017/2018 : GP of Moscow
By ko_osaga, history, 6 years ago, In English

WHERE IS IT?

Edit : Ok because of the delay we are unable to participate :/

  • Vote: I like it
  • +28
  • Vote: I do not like it

Comments Comments (40)
| Write comment?
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Where is it???

→ Reply
»
6 years ago, # |
  Vote: I like it +35 Vote: I do not like it

April Fools?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

We are in Moscow but we can't find the link too...

→ Reply
»
6 years ago, # |
  Vote: I like it +11 Vote: I do not like it

There is an onsite contest with the same problems (Moscode). I guess there was some trouble in the onsite contest.

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +26 Vote: I do not like it

https://official.contest.yandex.ru/opencupXVIII/contest/7895/enter : "The virtual contest is in progress. You are not allowed to participate"

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    Hi. How do you find this link? I couldn't find it at opencup.ru :(

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +89 Vote: I do not like it

      I used for i in `seq 7836 8000`; do wget "https://official.contest.yandex.ru/opencupXVIII/contest/$i/enter/"; done; in bash :/

      → Reply
»
6 years ago, # |
  Vote: I like it +32 Vote: I do not like it

According to snarknews, the contest will start one hour later, at 12:00 Moscow time.

→ Reply
»
6 years ago, # |
  Vote: I like it +49 Vote: I do not like it

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +10 Vote: I do not like it

Do anybody want to join today in team ext64 with me and savinov ?

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +15 Vote: I do not like it

7 minutes and still no link ?

UPD: this one

→ Reply
»
6 years ago, # |
  Vote: I like it +28 Vote: I do not like it

Where is 2nd division link?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

how to solve B,H, E?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +26 Vote: I do not like it

    B: For each added point, consider all the points within the square with length equals to the twice of current answer and centered at this point. Try all the possible triples. There won’t be too many points.

    H: dp[i][j]=min length of si - 1 when si=p[0..j]

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    H: dynamic programming: dp[i][k] — what is the minimal length of sk - 1 such that there exists sk of length exactly i (it also should be a prefix of p). How to invent that state: think of brute force, understand that we should know lengths of sk, sk - 1 in order to generate sk + 1, then swap answer with one of dimensions (here I swapped the answer with |sk - 1|).

    Now recalculation is simple: if you have sk with a specific length and you know |sk - 1|, then you know minimal possible length of tk + 1, and you also know its maximal length (it's minimal value of z-function and |sk|; if you forget about the latter, you get WA 12).

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +28 Vote: I do not like it

    It can always be achieved with at most two operations [1, n], [1, n - 1].

    So just check if it's possible to achieve in one operation. Otherwise, construct with the two intervals.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you explain how you do it in two operations?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        You can deduce each element one by one.

        For example, to make the sequence 10 4 3 5 7, the two constructed sequence should be 7 2 1 2 7 and 3 2 2 3

        → Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

D?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    If there are no boundaries at 0 and L, you take n functions yi(x) = ai ± x, and position of k-th dog at time t, is k-th sorted value of all yi(t).

    With boundaries answer is periodical over time with period 2L, so you should do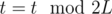 . Also you should add mirrored about the border lines and find k-th value in the interval [0, L]

    To find k - th value you can use binary search over answer, so you need to count number of yi <  = checkValue, and that's possible to do with 2 binary searches over lines of same type.

    That's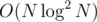

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      It's also possible to find k-th element of two merged arrays in O(logN) with few binary searches, instead of O(log2N).

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +23 Vote: I do not like it

      k-th value of union of two sorted arrays A and B in O(logn):

      Find the smallest i : A[i] >= B[k-i-1]. Return max(A[i-1], B[k-i-1]).

      Proof. We want to take k smallest numbers = i numbers from A and k-i numbers from B. Then the k-th value is f(i) = max(A[i-1], B[k-i-1]). f(i) decreases until B[k-i-1]  ≤  A[i] (i  →  i+1 means "change B[k-i-1] to A[i]").

      → Reply
»
6 years ago, # |
  Vote: I like it +36 Vote: I do not like it

How to solve C?

→ Reply
»
6 years ago, # |
  Vote: I like it +19 Vote: I do not like it

What is the expected solution for F ? I solved it with a general graph isomorphism algorithm.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +20 Vote: I do not like it

    Smart bruteforce + random?

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Here I give a seemingly rigorous solution:

    Suppose we can somehow identify vertices with value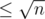 . The idea is that number of multiples for values in the range are distinct.

    Vertices not adjacent to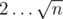 have value of prime number larger than . Call this set of vertices S.

    Then we can assign prime numbers greater than to S by its degree. e.g.: have same degree as the unknown vertices with value p1, p2, then we can arbitrarily give p1, p2 to v1, v2. Since somehow we cannot distinguish these 2 vertices.

    Now we identify all vertices with prime value. Hence we know prime factors each vertex has by its adjacent prime-valued vertices.

    The next step is to identify vertices with power of prime value (pe). Simply group vertices with single prime factor and sort them by degree, the larger degree the smaller exponent.

    For any other vertices, we can find exponents of its prime factors.

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    We tried the same, but failed to beat the TL. Can you share your code, please?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it +1 Vote: I do not like it

      Here is the code. The backtrack function (and maybe other parts of the code) may still have some bugs that do not happen in this case.

      Spoiler
      → Reply
»
6 years ago, # |
  Vote: I like it +18 Vote: I do not like it

How to solve A?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Concentrate on one player at a time, suppose the cards he ends up with are a1, ..., ak, with a1 being the best. Let bi be number of cards the previous player (the player who passes cards to the current player) has which are better than ai. Now process the cards of the current player from best to worst.

    Card i either initially belonged to some starting hand out of which the previous player just drafted a better card (bi options) or it was the first card drafted from the starting hand of the current player (1 option). Exactly i - 1 of these options have already been taken away (by previously processed (better) cards of the current player), so bi + 1 - (i - 1) options remain, resulting in a total of ways to choose where the cards for the current player came from.

    The only thing left is to make sure that the current player started with at least one card, so we need to subtract the number of ways in which we never choose the second type of option, which is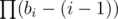 . The final answer is the product of the number of ways for each player. All this can be implemented in .

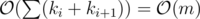    → Reply