Hi, CodeForces.
Recently I decided to take a closer look at data structure called Fenwick tree or binary indexed tree.
In this blogpost I will only consider Fenwick tree for sum, but everything stated there can be easily generalized for any associative, commutative and inversable operation.
After reading articles about it on e-maxx.ru and neerc.ifmo.ru and asking friends I've got interested by this moment. Both articles (and my friends) use this algorithm to initialize Fenwick tree on given array:
- Fenwick tree for array of zeros is array of zeros, we will take it as a basis
- We will use tree queries to replace all elements of array with elements we need
void init_vector_classic (vector<int> a) {
init_empty(a.size());
for (int i = 0; i < a.size(); i++) inc(i, a[i]);
}
This will work in O(N * logN) where N is length of given array.
Can we do it faster? Definitely can!
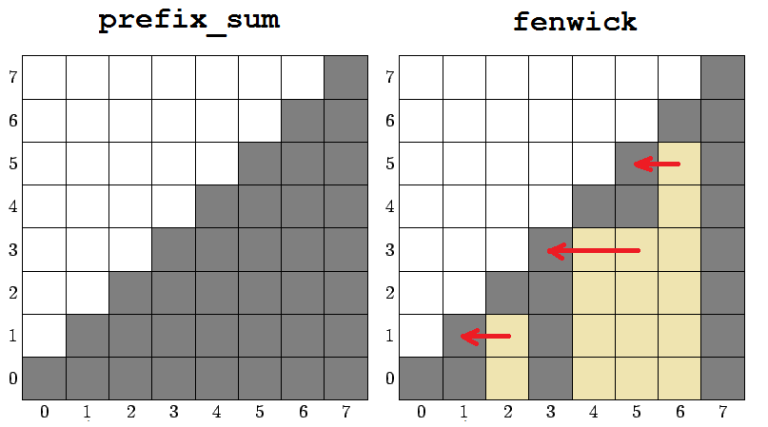
By definition of the Fenwick tree each tree element is the sum of continious segment of initial array. Considering that we have no queries to change elements in initialization process, we can use prefix sums to calculate elements of our Fenwick tree. This will require O(N) preprocessing, but will allow to calculate tree elements in O(1). So initialization asymptotic improves to O(N) + O(1) * O(N) = O(N).
void init_vector_linear_prefix (vector<int> a) {
init_empty(a.size());
vector<int> prefix_sum;
prefix_sum.assign(a.size(), 0);
prefix_sum[0] = a[0];
for (int i = 1; i < a.size(); i++) prefix_sum[i] = prefix_sum[i-1] + a[i];
for (int i = 0; i < a.size(); i++) {
int lower_i = (i & (i+1)) - 1;
fenwick[i] = prefix_sum[i] - (lower_i >= 0 ? prefix_sum[lower_i] : 0);
}
}
But in this implementation we get additional O(N) memory to store additional array.
Can we avoid this? Yes, we can!
We can notice that to initialize fenwick[i] we only require such elements of prefix_sum[j] where j ≤ i. This allows to use only one array and, starting from the end, change each element from prefix sum to Fenwick tree element.
void init_vector_linear (vector<int> a) {
init_empty(a.size());
fenwick[0] = a[0];
for (int i = 1; i < a.size(); i++) fenwick[i] = fenwick[i-1] + a[i];
for (int i = a.size()-1; i > 0; i--) {
int lower_i = (i & (i+1)) - 1;
if (lower_i >= 0) fenwick[i] -= fenwick[lower_i];
}
}
This way we can improve initialization time of Fenwick tree to O(N) using O(1) additional memory.
Of course, in most of the problems amount of queries is not much less than the size of Fenwick tree, so improving initialization time will not improve final asymptotic of your solution. But this optimization gives as ability to improve constant of the part of your solution, that works with Fenwick tree (or trees) with just a few lines of code.
What do you think about this and how do you initialize your Fenwick trees?
UPD: There is another approach to this problem that leads to even shorter code! Thanks Jakube for mentioning this in comments and sdnr1 for creating blog about it.










I'm also using a linear time construction for the Fenwick tree (although I haven't used a Fenwick tree in ages). Learned the method from Is it possible to build a Fenwick tree in O(n)?. This method approaches the construction of the array from the exact opposite direction.
Auto comment: topic has been updated by ATSTNG (previous revision, new revision, compare).
I think it is still $$$O(n)$$$ additional memory on it since you copying a new vector to the parameter
I prefer to use this
I am not sure why I am getting downvotes. I dont mind having nagative contribution but atleast can some one explain me about my mistakes ?
Because as what I can observe the code below will create a new array. And the additional memory complexity will raise to $$$O(n)$$$ and not $$$O(1)$$$.
While using reference or const-reference wont create a copy to the parametter so it should be $$$O(1)$$$ additional memory
What would happen if I use other function then just summing up elements, is there any dangerous corner cases or something ? Because I dont think there are always existing inverse function like adding $$$(+)$$$ have its inverse: subtract $$$(-)$$$ so it is better to build things bottom-up right ?
Does this function correct ?