Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for(int i = 0; i < int(n); i++)
using namespace std;
int main() {
long long n, m;
int a, b;
cin >> n >> m >> a >> b;
cout << min(n % m * b, (m - n % m) * a) << endl;
return 0;
}
Tutorial
Tutorial is loading...
Solution (adedalic)
#include<bits/stdc++.h>
using namespace std;
const int N = 200 * 1000 + 555;
int n, k, a[N];
inline bool read() {
if(!(cin >> n >> k))
return false;
for(int i = 0; i < n; i++)
assert(scanf("%d", &a[i]) == 1);
return true;
}
inline void solve() {
sort(a, a + n);
a[n++] = int(2e9);
int ans = 0, u = 0;
for(int i = 0; i < n - 1; i++) {
while(u < n && a[i] == a[u])
u++;
if(a[u] - a[i] > k)
ans++;
}
cout << ans << endl;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
int tt = clock();
#endif
if(read()) {
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
#endif
}
return 0;
}
990C - Bracket Sequences Concatenation Problem
Tutorial
Tutorial is loading...
Solution (Ajosteen)
#include <bits/stdc++.h>
using namespace std;
const int N = int(3e5) + 7;
int n;
string s[N];
char buf[N];
int cnt[N];
int getBalance(string &s){
int bal = 0;
for(int i = 0; i < s.size(); ++i){
if(s[i] == '(')
++bal;
else
--bal;
if(bal < 0)
return -1;
}
return bal;
}
string rev(string &s){
string revs = s;
reverse(revs.begin(), revs.end());
for(int i = 0; i < revs.size(); ++i)
if(revs[i] == '(')
revs[i] = ')';
else
revs[i] = '(';
return revs;
}
int main(){
scanf("%d", &n);
for(int i = 0; i < n; ++i){
scanf("%s", buf);
s[i] = buf;
}
for(int i = 0; i < n; ++i){
int bal = getBalance(s[i]);
if(bal != -1)
++cnt[bal];
}
long long res = 0;
for(int i = 0; i < n; ++i){
s[i] = rev(s[i]);
int bal = getBalance(s[i]);
if(bal != -1)
res += cnt[bal];
}
printf("%I64d\n", res);
return 0;
}
990D - Graph And Its Complement
Tutorial
Tutorial is loading...
Solution (Ajosteen)
#include <bits/stdc++.h>
using namespace std;
const int N = int(1e3) + 7;
int n, a, b;
bool mat[N][N];
int main(){
scanf("%d %d %d", &n, &a, &b);
if(min(a, b) > 1){
puts("NO");
return 0;
}
if(a == 1 && b == 1){
if(n == 2 || n == 3){
puts("NO");
return 0;
}
puts("YES");
for(int i = 1; i < n; ++i)
mat[i][i - 1] = mat[i - 1][i] = true;
for(int i = 0; i < n; ++i){
for(int j = 0; j < n; ++j)
printf("%c", '0' + mat[i][j]);
puts("");
}
return 0;
}
bool x = false;
if(a == 1){
swap(a, b);
x = true;
}
for(int i = n - a; i > 0; --i)
mat[i][i - 1] = mat[i - 1][i] = true;
puts("YES");
for(int i = 0; i < n; ++i){
for(int j = 0; j < n; ++j)
printf("%c", '0' + ((x ^ mat[i][j]) && (i != j)));
puts("");
}
return 0;
}
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int INF = 1e9;
const long long INF64 = 1e18;
const int N = 1000 * 1000 + 13;
int n, m, k;
bool pos[N];
int lst[N], s[N], a[N];
int get(int l){
int r = 0, i = -1, res = 0;
while (r < n){
if (lst[r] <= i)
return INF;
i = lst[r];
r = lst[r] + l;
++res;
}
return res;
}
int main() {
scanf("%d%d%d", &n, &m, &k);
forn(i, m) scanf("%d", &s[i]);
forn(i, k) scanf("%d", &a[i]);
forn(i, n) pos[i] = true;
forn(i, m) pos[s[i]] = false;
forn(i, n){
if (pos[i])
lst[i] = i;
else if (i)
lst[i] = lst[i - 1];
else
lst[i] = -1;
}
long long ans = INF64;
forn(i, k){
long long t = get(i + 1);
if (t != INF)
ans = min(ans, a[i] * t);
}
printf("%lld\n", ans == INF64 ? -1 : ans);
return 0;
}
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
mt19937 rnd(time(NULL));
const int N = 1'000'013;
int n, m;
pair<int, int> e[N];
int a[N], rk[N];
long long sum[N], ans[N];
int p[N];
int getP(int a){
return (a == p[a] ? a : p[a] = getP(p[a]));
}
bool merge(int a, int b){
a = getP(a);
b = getP(b);
if (a == b) return false;
if (rk[a] > rk[b]) swap(a, b);
p[a] = b;
rk[b] += rk[a];
return true;
}
bool used[N];
vector<int> g[N];
int h[N];
void dfs(int v, int p){
sum[v] = a[v];
for (auto u : g[v]){
if (u != p){
h[u] = h[v] + 1;
dfs(u, v);
sum[v] += sum[u];
}
}
}
int main() {
scanf("%d", &n);
forn(i, n)
scanf("%d", &a[i]);
forn(i, n) p[i] = i, rk[i] = 1;
scanf("%d", &m);
forn(i, m){
int &v = e[i].first;
int &u = e[i].second;
scanf("%d%d", &v, &u);
--v, --u;
if (merge(v, u)){
g[v].push_back(u);
g[u].push_back(v);
used[i] = true;
}
}
long long tot = 0;
forn(i, n) tot += a[i];
if (tot != 0){
puts("Impossible");
return 0;
}
dfs(0, -1);
puts("Possible");
forn(i, m){
if (used[i]){
int v = e[i].first, u = e[i].second;
if (h[v] < h[u])
ans[i] = sum[u];
else
ans[i] = -sum[v];
}
printf("%lld\n", ans[i]);
}
return 0;
}
Tutorial
Tutorial is loading...
Solution with Möbius (Bleddest)
#include<bits/stdc++.h>
using namespace std;
const int N = 200043;
int d[N];
void sieve()
{
vector<int> pr;
for(int i = 2; i < N; i++)
{
if (d[i] == 0)
{
d[i] = i;
pr.push_back(i);
}
for(auto x : pr)
{
if (x > d[i] || x * 1ll * i >= N)
break;
d[i * x] = x;
}
}
}
int mobius(int x)
{
int last = -1;
int res = 1;
while(x != 1)
{
if(last == d[x])
res = 0;
else
res = -res;
last = d[x];
x /= d[x];
}
return res;
}
int mb[N];
vector<int> need_bfs[N];
int used[N];
vector<int> g[N];
int a[N];
int cc = 0;
int q[N];
int hd, tl;
int good[N];
int bfs(int x, int gc)
{
hd = 0;
tl = 0;
q[tl++] = x;
used[x] = cc;
while(hd < tl)
{
int z = q[hd++];
for(auto y : g[z])
{
if(good[a[y]] == cc && used[y] < cc)
{
used[y] = cc;
q[tl++] = y;
}
}
}
return tl;
}
long long ans1[N];
long long ans2[N];
int main() {
sieve();
for(int i = 1; i < N; i++)
mb[i] = mobius(i);
int n;
scanf("%d", &n);
for(int i = 0; i < n; i++)
scanf("%d", &a[i]);
for(int i = 0; i < n - 1; i++)
{
int x, y;
scanf("%d %d", &x, &y);
--x;
--y;
g[x].push_back(y);
g[y].push_back(x);
}
for(int i = 0; i < n; i++)
{
need_bfs[a[i]].push_back(i);
}
for(int i = 200000; i >= 1; i--)
{
cc++;
for(int j = i; j <= 200000; j += i)
good[j] = cc;
for(int j = i; j <= 200000; j += i)
for(auto x : need_bfs[j])
{
if(used[x] == cc) continue;
int z = bfs(x, i);
ans1[i] += z * 1ll * (z + 1) / 2;
}
for(int j = i, k = 1; j <= 200000; j += i, k++)
ans2[i] += mb[k] * ans1[j];
}
for(int i = 1; i <= 200000; i++)
if(ans2[i])
printf("%d %lld\n", i, ans2[i]);
return 0;
}
Solution with centroid (adedalic)
#include<bits/stdc++.h>
using namespace std;
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define x first
#define y second
typedef long long li;
typedef long double ld;
typedef pair<int, int> pt;
template<class A, class B> ostream& operator <<(ostream &out, const pair<A, B> &p) {
return out << "(" << p.x << ", " << p.y << ")";
}
template<class A> ostream& operator <<(ostream &out, const vector<A> &v) {
out << "[";
for(auto &e : v)
out << e << ", ";
return out << "]";
}
const int N = 1000 * 1000 + 555;
const int LOGN = 21;
int mind[N];
int pw[LOGN][N];
int n, a[N];
vector<int> g[N];
li res[N];
bool gen() {
mt19937 rnd(42);
n = 200 * 1000;
fore(i, 0, n)
a[i] = 831600;
fore(i, 1, n) {
int u = rnd() % i, v = i;
g[u].push_back(v);
g[v].push_back(u);
}
return true;
}
inline bool read() {
// return gen();
if(!(cin >> n))
return false;
fore(i, 0, n)
assert(scanf("%d", &a[i]) == 1);
fore(i, 0, n - 1) {
int u, v;
assert(scanf("%d%d", &u, &v) == 2);
u--, v--;
g[u].push_back(v);
g[v].push_back(u);
}
return true;
}
vector<pt> dv[N];
inline int gcd(int a, int b) {
int ans = 1;
unsigned int u = 0, v = 0;
while(u < dv[a].size() && v < dv[b].size()) {
if(dv[a][u].x < dv[b][v].x)
u++;
else if(dv[a][u].x > dv[b][v].x)
v++;
else {
ans *= pw[min(dv[a][u].y, dv[b][v].y)][dv[a][u].x];
u++, v++;
}
}
return ans;
}
bool used[N];
int sz[N];
void calcSz(int v, int p) {
sz[v] = 1;
for(int to : g[v]) {
if(to == p || used[to])
continue;
calcSz(to, v);
sz[v] += sz[to];
}
}
int findC(int v, int p, int all) {
for(int to : g[v]) {
if(to == p || used[to])
continue;
if(sz[to] > all / 2)
return findC(to, v, all);
}
return v;
}
int u[N], T = 0;
int cntD[N];
inline void addDiv(int d, int cnt) {
if(u[d] != T)
u[d] = T, cntD[d] = 0;
cntD[d] += cnt;
}
int cds[N], szcds;
void calcDs(int v, int p, int gc) {
gc = gcd(a[v], gc);
cds[szcds++] = gc;
for(int to : g[v]) {
if(to == p || used[to])
continue;
calcDs(to, v, gc);
}
}
vector<int> cps, cmx, vmx;
void check(int curd, int curg, int pos, int add) {
if(pos >= (int)cps.size()) {
if(u[curd] == T)
res[curg] += cntD[curd] * 1ll * add;
return;
}
fore(st, 0, cmx[pos] + 1) {
check(curd, curg, pos + 1, add);
curd *= cps[pos];
if(st < vmx[pos])
curg *= cps[pos];
}
}
pt ops[N]; int szops;
int cntDiff[N];
void calc(int v) {
calcSz(v, -1);
int c = findC(v, -1, sz[v]);
used[c] = 1;
// cerr << "C = "<< c << endl;
cps.resize(dv[a[c]].size());
cmx.resize(cps.size());
vmx.resize(cmx.size());
fore(i, 0, cps.size()) {
cps[i] = dv[a[c]][i].x;
cmx[i] = dv[a[c]][i].y;
}
T++;
addDiv(a[c], 1);
for(int to : g[c]) {
if(used[to]) continue;
szcds = 0;
calcDs(to, c, a[c]);
fore(i, 0, szcds)
cntDiff[cds[i]]++;
szops = 0;
fore(j, 0, szcds) {
if(cntDiff[cds[j]] == 0)
continue;
int p = 0, val = cds[j];
fore(i, 0, vmx.size()) {
if(p >= (int)dv[val].size() || dv[val][p].x > cps[i])
vmx[i] = 0;
else
vmx[i] = dv[val][p].y, p++;
}
check(1, 1, 0, cntDiff[cds[j]]);
ops[szops++] = {cds[j], cntDiff[cds[j]]};
cntDiff[cds[j]] = 0;
}
fore(j, 0, szops)
addDiv(ops[j].x, ops[j].y);
}
for(int to : g[c]) {
if(used[to]) continue;
calc(to);
}
}
inline void solve() {
iota(mind, mind + N, 0);
fore(i, 2, N) {
if(mind[i] != i)
continue;
pw[0][i] = 1;
fore(st, 1, LOGN)
pw[st][i] = pw[st - 1][i] * i;
for(li j = i * 1ll * i; j < N; j += i)
mind[j] = min(mind[j], i);
}
fore(i, 2, N) {
int val = i;
while(mind[val] > 1) {
if(dv[i].empty() || dv[i].back().x != mind[val])
dv[i].emplace_back(mind[val], 0);
dv[i].back().y++;
val /= mind[val];
}
}
memset(res, 0, sizeof res);
T = 0;
calc(0);
fore(i, 0, n)
res[a[i]]++;
fore(i, 1, 1000'000 + 1) {
if(res[i])
printf("%d %lld\n", i, res[i]);
}
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
int tt = clock();
#endif
if(read()) {
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
#endif
}
return 0;
}










Can someone explain a bit more about the complexity for the problem E "Post Lamps" ?
Essentially it uses the fact that the sum of reciprocials of numbers up to n is about ln(n) for large n. The proof outline is as follows. We start from the fact (1+1/n)^n<e<(1+1/n)^(n+1). Now by taking logarithm we get that 1/(1+n)<ln(1+1/n)<1/n. Summing over all n gives desired.
I passed GCD Counting with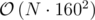 . Was a solution with that complexity intended to pass?
. Was a solution with that complexity intended to pass?
Was your solution for each subtree, calculate number of paths into the current node with each gcd and then find the contribution of each pair of paths from different subtrees? I wrote such a solution but I believe the complexity can be bounded by 160 N log N. This is for the case of a k-ary tree where we have f(N) = k f(N/k) + 160 N. Other trees only seem to require less operations — a line graph is only 160N.
In Problem G , solution with centroid's code , there's an extra " ' " in the countdown fifth line of function "solve()" .
Digit separators
Thx . I seldom use C++14
But I think you should consider removing it from the model solution as it looks like it's not being displayed correctly on codeforces. The entire code after the seperator is having a green color which is very confusing for someone trying to read the solution. Seems like cf cannot display this feature correctly for code in markdown.
in problem E the answer of first example ,if I let the lamp has 1 power place in position 0 2 4 5 then segment【0;n】 can be covered ,the answer is 4 why?
Answer to the most common question
awoo Can you explain the complexity of your " get " function for the problem E Post Lamps ?
get(i) takes about steps to finish. Then it's the same as in Eratosthenes sieve, for example.
steps to finish. Then it's the same as in Eratosthenes sieve, for example. 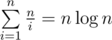 in total.
in total.
I think it takes more than n / i steps for every i since we are not iterating on the multiples of i. But I am not able to bound it to n / i . Can you give an explanation for the bounding part ?
It takes more than but it is
but it is 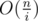 . Try doing two steps. You put segment, find the next free position, put another segment. Either the next free position will be i + 1 away from the first one, or you will quit function immediately. Then you reach n in about
. Try doing two steps. You put segment, find the next free position, put another segment. Either the next free position will be i + 1 away from the first one, or you will quit function immediately. Then you reach n in about  steps with some constant factor.
steps with some constant factor.
May be, We can block some positions such that every i (1 to k) will take O(n) steps. Won't that make this algorithm O(n*k) which will TLE. Or can we always prove that complexity is O(n*lg(n)) ?
OMG, guys, can't you like draw it yourselves?
Imagine the worst case for placing two segments. It's when there are just two free positions and then lots of blocked ones. So you put one to the first position, one to the second position and then you will go right to l + 1 from the first free position or there will be no free spaces.
y = 0 is the axis (black is blocked, white is free). The other two are two placed segments.
You can draw other cases with less blocked positions, with more free positions to the left and see that the case I drew is the worst of them.
Understood. Thanks a lot :)
In G; anyone care to explain how this relation is derived?
We can use inclusion-exclusion to get the following:
The number of such sets is infinite, but since for every p(S) > 2·105 h(p(S)) = 0, we can iterate on the numbers from 1 to 2·105 and check whether there exists some set such that p(S) is equal to this number.
In fact, if some number x is divisible by some number q2 (where q is prime), then there is no set S such that p(S) = x (and μ(x) = 0). Otherwise, there is exaclty one set which is the factorization of x, and μ(x) = - 1 if and only if the size of this set is an odd number.
Is this explanation clear? Or should I clarify something?
Right. The first sentence was the missing link I needed, thanks a lot!
For a way that relies more on the mobius inversion, it's easy to see that
To see this, take h(5). The number of paths whose gcd is divisible by 5 are all the paths who have a gcd of 5, 10, 15, 20, etc. Now, there's an alternate form of the mobius inversion that states that
Thus, to get a formula for ans, it's simply
As an explanation for this alternate form, take a look at https://math.stackexchange.com/questions/1965342/does-the-mobius-inversion-theorem-hold-when-sum-function-is-over-multiples-inste
Different answer for same code 1. http://codeforces.com/contest/990/submission/39189478 2. https://ideone.com/XWY4uR
At line 41 Use :
int cntop[maxn]={0}, cntcl[op] ={0};
Instead :
int cntop[maxn], cntcl[op] ;
rep(i,maxn) cntop[i] = cntcl[i] = 0 ;
No that was not the problem. cntcl[op] -> cntcl[maxn]
Can someone explain the solution with centroid decompression in the problem G?
Key idea of this solution is next: let's look at the subtree in decomposition with its centroid c. You need to calculate all paths which go throw c, so its gcd will be divisors of a[c] and there will be no more than K different divisors of a[c] (K ≤ 160). So if you process each subtree (subtrees are formed by childs of c) not with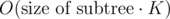 but with
but with 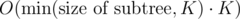 (checking each gcd still takes O(K) operations) complexity will reduce from
(checking each gcd still takes O(K) operations) complexity will reduce from 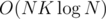 to something like
to something like 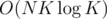 .
.
Apparently a centroid decomposition involves recursively finding the centroid of each subtree, so this is not actually a centroid decomposition since the centroid is found only once. I believe this is only a constant-factor speedup over the naive O(NK log N) solution I described here, which was fast enough, runs in about 1 second.
I could miss something, but my proof was next: Let's look at all subtrees, which appeared in decomposition.
Proposition: there O(N / K) subtrees with size at least K (let's name them big). To prove it, let's find all big subtrees which don't contain any other big subtree. There is no more than N / K such subtree. Let it will be 0-level. Let's look at subtrees, which contains 0-level subtrees. Name them 1-level. Since it's centroid decomposition size of each subtree of 1-level at least twice of size of 0-level. So there are no more than N / 2K such subtrees. And so on. So there no more than N / K + N / 2K + N / 4K... = O(N / K). Each big subtree is processes with O(K2) time. So total complexity for big subtrees is O(N / K·K2) = O(NK).
Similarly, There are O(N) small subtrees, but each small subtree of size x is processed with O(xK) time. But there are no more than levels of small subtrees since after that they become big and each level is processed with O(NK) in total. Here we came to final
levels of small subtrees since after that they become big and each level is processed with O(NK) in total. Here we came to final 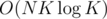 complexity. Of course there is also
complexity. Of course there is also  to build decomposition and
to build decomposition and  or
or 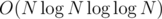 to calculate gcd-s.
to calculate gcd-s.
Ah, I think I misunderstood your last comment. It seems you are using a legit centroid decomposition, so the complexity makes sense. At first I didn't understand how centroids would work, since you calculate paths to the middle, but then for the parent calculation you need a different set of paths. But I guess you could find most of those by taking the gcd of the path to the centroid and the path from the centroid to its parent.
I think that tests for problem E are weak, because my (I think!) wrong solution passed. I'll try to explain my logic:
Firstly, note that F(i) (editorial explanation) is decreasing with an increase i.
Second, assign every a[i] to min(a[j]), i <= j (obviously???)
a[i] is increasing with an increase i.
So we have two functions F(i) and a[i], answer for fixed i is F(i) * a[i].
Now every a[i] change to - a[i].
So we have two decreasing functions.
Now launch ternary search xD
Answer is maximum F(i) * a[i] multiplied by -1 (because we changed a[i] to - a[i]).
Please hack me, because no one was trying to do it (maybe, I'm a lucky one)
I found a hack to your solution.
Your program outputs 720720000 while the correct answer should be 199*(720720/2)=71711640
I chose 720720 because it is the LCM of 1..16 so the first numbers all divide evenly into N. Then, you make the first few numbers cost equal to its size, so they all cost the same, so ternary search can't find the one that costs slightly below it's size. I padded on the 100000s so that it won't run into your brute force when the range is too small.
nice
Can anyone explain E? I struggling going through it. And why he has chosen this approach and its proof? Help!
It goes like this. You come up with straightforward O(n3) dp solution. Then you check the constraints and decide that there should be a greedy solution, not a dp one. After that you check which states are actually useful when updating the next states. Finally, you code it greedy using some precalc values to achieve the right complexity.
The proof can be found in earlier comments of this blog.
can anyone please explain problem C? I am not able to get the intuition to it from the editorial. Thanks in advance !
Concerns about Problem: E Post Lamps.
Why are all the lamps being considered? Should not only ONE lamp with power >= 'some value L' and having the least cost be the optimal choice?
e.g: Suppose the maximum length of consecutive forbidden positions is 'L'. Then we must use a lamp with a power of at least 'L+1'. (We may put this lamp just before the start of that forbidden segment).
Now isn't it better to use a lamp with a power greater than 'L+1', but having a smaller cost? But this is not giving the optimal answer for some reason. I can not seem to find any example where a greater powered less cost lamp is not giving better answer.
Let array of costs be increasing array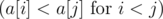 . For each L there are no ''a greater powered less cost lamp'', but optimal answer can be any of L.
. For each L there are no ''a greater powered less cost lamp'', but optimal answer can be any of L.
Thank you for your response.
I am getting it now.
Here is the case that I was missing:
pattern: 0XXXXX000
lamp1: power: 6 , cost: 10 , ans: 2*10 = 20 ( 2 piece needed )
lamp2: power: 8 , cost: 11 , ans: 1*11 = 11 ( 1 piece needed )
Optimal answer is obtained by lamp2.
I finally managed to pass tests with my solution for G. It is stupid dp on trees technique dp[v] = sack with pairs <gcd number, amount of paths>. Dp counted bottom-up then top-down. I think it can be hacked by ML verdict with careful test. Submission
For F, visualize the graph as follows. Add two extra nodes, a source node from which water comes and a sink node to which water flows. For the remaining nodes if a node has a positive value of Si then water is flowing out of the node to the sink node and if it has a negative value of Si water is flowing into the node from the source node. All that we need to do now is to balance the flow. In order to do this, find a spanning tree of the graph and then for each node, calculate how much water should flow into/out of it's subtree, add the input/output of the current node and pass the remaining water to it's parent. Reference code: http://codeforces.com/contest/990/submission/40238544