I'm really sorry for the issue with the problem D difficulty, it was much harder than i expected, and there was a big difficulty gap between problems C and D. I hope in the next rounds it will never happen again.
UPD: I'd like to say a big thanks to kevinsogo for the great help with tutorials and the round preparation in general.
Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, k;
cin >> n >> k;
vector<int> a(n);
for (int i = 0; i < n; ++i)
cin >> a[i];
int ans = 0;
while (!a.empty() && a.back() <= k) {
++ans;
a.pop_back();
}
reverse(a.begin(), a.end());
while (!a.empty() && a.back() <= k) {
++ans;
a.pop_back();
}
cout << ans << endl;
return 0;
}
Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n;
string s;
cin >> n >> s;
for (int i = 1; i <= n; ++i) {
if (n % i == 0) {
reverse(s.begin(), s.begin() + i);
}
}
cout << s << endl;
return 0;
}
Tutorial
Tutorial is loading...
Solution 1 (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, k;
cin >> n >> k;
string s;
cin >> s;
vector<int> cnt(26);
for (auto c : s) ++cnt[c - 'a'];
int pos = 26;
for (int i = 0; i < 26; ++i) {
if (k >= cnt[i]) {
k -= cnt[i];
} else {
pos = i;
break;
}
}
string ans;
int rem = k;
for (auto c : s) {
int cur = c - 'a';
if (cur > pos || (cur == pos && rem == 0)) {
ans += c;
} else if (cur == pos) {
--rem;
}
}
cout << ans << endl;
return 0;
}
Solution 2 (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, k;
cin >> n >> k;
string s;
cin >> s;
vector<pair<char, int>> c(n);
for (int i = 0; i < n; ++i)
c[i] = make_pair(s[i], i);
sort(c.begin(), c.end());
sort(c.begin() + k, c.end(), [&] (const pair<char, int> &a, const pair<char, int> &b) {
return a.second < b.second;
});
for (int i = k; i < n; ++i)
cout << c[i].first;
cout << endl;
return 0;
}
999D - Equalize the Remainders
Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, m;
cin >> n >> m;
int k = n / m;
vector<int> a(n);
vector<vector<int>> val(m);
for (int i = 0; i < n; ++i) {
cin >> a[i];
val[a[i] % m].push_back(i);
}
long long ans = 0;
vector<pair<int, int>> fre;
for (int i = 0; i < 2 * m; ++i) {
int cur = i % m;
while (int(val[cur].size()) > k) {
int elem = val[cur].back();
val[cur].pop_back();
fre.push_back(make_pair(elem, i));
}
while (int(val[cur].size()) < k && !fre.empty()) {
int elem = fre.back().first;
int mmod = fre.back().second;
fre.pop_back();
val[cur].push_back(elem);
a[elem] += i - mmod;
ans += i - mmod;
}
}
cout << ans << endl;
for (int i = 0; i < n; ++i)
cout << a[i] << " ";
cout << endl;
return 0;
}
999E - Reachability from the Capital
Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
const int N = 5010;
int n, m, s;
vector<int> g[N];
bool used[N];
bool ok[N];
int cnt;
void dfs1(int v) {
ok[v] = true;
for (auto to : g[v])
if (!ok[to])
dfs1(to);
}
void dfs2(int v) {
used[v] = true;
++cnt;
for (auto to : g[v])
if (!used[to] && !ok[to])
dfs2(to);
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
cin >> n >> m >> s;
--s;
for (int i = 0; i < m; ++i) {
int x, y;
cin >> x >> y;
--x, --y;
g[x].push_back(y);
}
dfs1(s);
vector<pair<int, int>> val;
for (int i = 0; i < n; ++i) {
if (!ok[i]) {
cnt = 0;
memset(used, false, sizeof(used));
dfs2(i);
val.push_back(make_pair(cnt, i));
}
}
sort(val.begin(), val.end());
reverse(val.begin(), val.end());
int ans = 0;
for (auto it : val) {
if (!ok[it.second]) {
++ans;
dfs1(it.second);
}
}
cout << ans << endl;
return 0;
}
Linear Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
const int N = 5010;
int n, m, s;
vector<int> g[N];
vector<int> tg[N];
vector<int> cg[N];
vector<int> ord;
int indeg[N];
bool ucomp[N];
bool used[N];
int comp[N];
int cnt;
void dfs1(int v) {
used[v] = true;
for (auto to : g[v])
if (!used[to])
dfs1(to);
ord.push_back(v);
}
void dfs2(int v) {
comp[v] = cnt;
for (auto to : tg[v])
if (comp[to] == -1)
dfs2(to);
}
void dfs3(int v) {
ucomp[v] = true;
for (auto to : cg[v])
if (!ucomp[to])
dfs3(to);
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
cin >> n >> m >> s;
--s;
for (int i = 0; i < m; ++i) {
int x, y;
cin >> x >> y;
--x, --y;
g[x].push_back(y);
tg[y].push_back(x);
}
for (int i = 0; i < n; ++i) {
if (!used[i]) {
dfs1(i);
}
}
reverse(ord.begin(), ord.end());
memset(comp, -1, sizeof(comp));
for (int i = 0; i < n; ++i) {
if (comp[ord[i]] == -1) {
dfs2(ord[i]);
++cnt;
}
}
for (int v = 0; v < n; ++v) {
for (auto to : g[v]) {
if (comp[v] != comp[to]) {
cg[comp[v]].push_back(comp[to]);
++indeg[comp[to]];
}
}
}
dfs3(comp[s]);
int ans = 0;
for (int i = 0; i < cnt; ++i)
if (!ucomp[i] && indeg[i] == 0)
++ans;
cout << ans << endl;
return 0;
}
Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
const int N = 520;
const int K = 12;
const int C = 100 * 1000 + 11;
int n, k;
int c[C];
int f[C];
vector<int> h;
int dp[N][K * N];
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
cin >> n >> k;
h = vector<int>(k + 1);
for (int i = 0; i < n * k; ++i) {
int x;
cin >> x;
++c[x];
}
for (int i = 0; i < n; ++i) {
int x;
cin >> x;
++f[x];
}
for (int i = 1; i <= k; ++i)
cin >> h[i];
for (int i = 0; i < n; ++i) {
for (int j = 0; j <= n * k; ++j) {
for (int cur = 0; cur <= k; ++cur) {
dp[i + 1][j + cur] = max(dp[i + 1][j + cur], dp[i][j] + h[cur]);
}
}
}
int ans = 0;
for (int i = 0; i < C; ++i) {
if (f[i] != 0) ans += dp[f[i]][c[i]];
}
cout << ans << endl;
return 0;
}











Thanks for the editorial, and interesting problems, surely we get to learn something!!
Thanks for the editorial
My ideia on 999E - Reachability from the Capital is as follows:
Great contest! :) 39522069
You don't need DFS for each element in the set, the answer is the number of SCC with 0 in degree. All SCC with > 0 in degree will be reached by some vertex, so it is not good to add edges between the capital and some vertex in a SCC with > 0 in degree.
What is D complexity? I think O(2*m + n)
O, i wanted to write the time complexity for each of the described solutions and forget about it :( I will do it now :)
vovuh, in D if the problem were adjusted so that we can increase/decrease the numbers, can it still have a greedy solution or even DP, It can be solved by Max-flow min-cut but with the constraints adjusted, any idea?
I thought about it right now, with increase\decrease the elements this problem can be solved at least by mincost maxflow (but this is most stupid idea, i will think about it more time and may be i will find better solution)
vovuh please feel free to update me here once you've arrived at something.
would anyone provide binary search solution for D as mentioned in tags
I think this would be proper, I'm using
std::setthough to find the nearest number that has less thann / mnumbers to fill from the current number I'm at with numbers> n / m39484134Mostly the tags include concepts that can be used, it doesn't mean that their obvious strict implementation is intended but rather the way they work in a certain condition, hope this is clear!
how should i start practicing for problem D, i am not able to solve them ?? (please don't go with my color).
How can I judge the Kyubi??
Let's start with the simple facts:
1) numbers themselves aren't important, we only care about their modulus to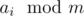 )
)
m(i.e.2) count the numbers that have the same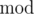 and store their indices in the original array
and store their indices in the original array
3) now iterate from 0 to m - 1(i.e. all possible mods under m) and if you have a mod that has numbers more than k = n / m store them somewhere call is Large, also store the numbers than have less than k = n / m in a set(or any container that supports finding the nearest number) call it Small
4)now for each number in Large in increasing order, call
X = count(large[i]) - n / mand you already know the mod of large[i] call itZ, now try to find the nearest mod in Small that is larger thanZin a cyclic order(i.e. if Z = m — 1, then search in[0, Z - 1]) call what you foundVand replace the index of this number with any number that have mod = V, do this for all X numbers in large[i].5) now to the proving part, since the problem tells you that you can only increase the numbers you have a greedy solution, why? because assume you have at index
inumbers than are larger than group size k, these numbers have to go to some modulus other thani(preferably near) in the direction from[i + 1, m - 1]then[0, i - 1], so you find the nearest modulus that have count < group size(k) and replace, this way you chose the best for indexinow go on with the next and so on, to prove this is optimal, suppose there's another index larger than i with count > group size(k) and you decided to go with it first before finding the answer for i first, now suppose you found the answer for that other index and replaced, nowiwill still have to move much more steps to reach a valid number with count < group size(k), thus our choice of larger index first was wrong, hence the optimal way is to use modulus in increasing cyclic order.submission: 39484134
Thanks for your proof. But I still have a small quetion. XD
In step 5), why
ihave to move much more steps to reach a valid number withcount < group size(k)if we found the answer for another index larger thaniwithcount > group size(k)and replaced ?Could you please give me some counterexamples ? :)
N = 8, M = 4, K = 20 4 12 1 5 8 9 13Now numbers wih respect to mod M, are[4, 4, 0, 0]If you solved forThanks for your example. XD
In your example, if we sloved for
i mod m = 1first, numbers with respect tomod Mare[2, 2, 2(from 1), 2(from 0)], which the total steps are 2 * (2 - 1) + 2 * (3 - 0) = 8. If we sloved fori mod m = 0first, numbers with respect tomod Mare[2, 2, 2(from 0), 2(from 1)], which the total steps are 2 * (2 - 0) + 2 * (3 - 1) = 8, too.Does this prove that we are correct in using modulus in either increasing or decreasing cyclic order? :)
Looking forward to your reply!
Ops! Perhaps this example was a bit weak to prove my point, and you can process mods in decreasing direction, as long as you're finding the nearest valid choice in increasing order a(i.e. a mod higher than the one you're currently processing in cyclic order of course), that last example was a proof for that.
Here's a modified version of the counter example The mods array
[4, 0, 4, 0]you can processi = 2, 0in either increasing or decreasing cyclic order, but you cannot replace i = 1, with i = 2, because you now have to go through[2, m - 1]then to[0, 1]which is clearly not optimal.Got it. Thanks for your detailed explanation! :)
thank you for your detailed solution .
from kyubi.
For Question E , Why wouldn't the following solution work?(I'm getting WA):
Answer is the No. of connected components in all the vertices that aren't reachable from s.
First find all the unreachable vertices from s. Find the no. of strongly connected components among the vertices (using all the edges).
You should find only SCC-s with indegree equal to 0.
Indegree of a Strongly Connected component? Can you explain a little further? Help is appreciated.
I ment indegree of SCC in the condensed graph(if you don't know the concept fill free to ask). Indegree is number of incoming edges.
To find indegrees of SCC-s we can go through all edges(u->v). If u and v belong to the same SCC then we do nothing. Else we increase indegree of the SCC containing v by 1.
Emil_PhysMath What is the meaning of graph condensation? What are its uses?
Thanks in advance..
Strongly connected component(SCC) is subset of vertices such that any two vertices of this subset are reachable from each other. It is obvious that any vertice belongs to exactly 1 SCC. Thus we can divide the graph into SCC-s. Condensation graph is graph containing every SCC as one vertex. There is an oriented edge between two vertices SCCi and SCCj of the condensation graph if and only if there are two vertices u∈SCCi,v∈SCCj such that there is an edge(u;v) in initial graph. The most important property of the condensation graph is that it is acyclic.
You can read about SCC and condensation graph here.
You are welcome. If you have a question, feel free to ask. :)
sir i am still unclear with the idea of using SCC , what is wrong in that , if we find the reachable cities
from capital using dfs and then connect other from capital and print the count . i mean just find connected component . i know , i am missing one or two things ,please help
thanks in advance !
At first we build the condensation graph(which is acyclic). Now we can connect the capital to all SCC-s with indegree equal to 0(but we will not connect capitals SCC to itself). Note that if we can get to vertex u in some SCC, then we can get to all other vertexes in that SCC.
Because if indegree of a SCC is equal to 0, we can't get there from the capital(it is obvious). So if their are k SCC-s with indegree equal to 0, we'll have to build at least k roads.
Let's assume that we can't get to SCC u. Now if its indegree equals to 0 then we will build a road between it and capital and live happy. Else there is an edge (u1->u). We'll do the same with u1. As condensation graph is acyclic we will never get to the same vertex=>at last we will get to the capital ot to SCC with indegree equal to 0 and live happy.
39490721 Remove the comments, the code itself isn't very complicated ;)
But I can't anderstand your approach.
i mean just find connected componentyou mean to find SCC-s?P.S. You are welcome :)
Connected component of a directed graph has 2 definitions.
1)SCC.
2)It is weakly connected if it would be connected by ignoring the direction of edges.
If you find number of connected components of type 2 you will not get the right answer.
Your answer would be 1, while the true answer is 2.
Their is no other definition of connected component, if you used some other concept as connected component, please, tell about it in comments.
sir can you tell me what is wrong with this approach? what i am trying to do is, run a dfs from the capital city and mark all the reachable nodes visited. Now , we again run dfs on those nodes which are not reachable from the capital city but we will not mark this node as visited. Example, if 2 is not reachable from capital city then we will run a dfs from 2 and will mark all the cities reachable from 2 as visited except for 2. And later, lets say 3 is also not reachable from capital city, so we run a dfs on 3 as well and mark all nodes reachable from it as visited except for 3.If 2 ,which was not marked visited initially , is reachable from 3 then 2 will be marked as visited. Finally we run a loop for all nodes and if a node is not visited just increment the final count. below is my solution 39578066
the_halfbloodprince, your program fails on test case below.
1
2
Here is your mistake: After _dfs-s from nodes 1,2,3 _dfs from node 4 is called. It goes to node 3 which is already visited=>doesn't go to node 2, so node 2 remains unvisited.
I am thinking how to fix it. If I have an idea I'll type it in comments
the_halfbloodprince, you need two arrays visited instead of one. In _dfs function you will use the second array, and before calling _dfs in main() you will have to fill it with value false. And after calling _dfs: if for node u visited2[u]==true you will assign true to visited1[u]: visited1[ind]=true.
39601152. Finally AC!!! :)
Emil_PhysMath Thanks for your answer sir.Now, i got it.
the_halfbloodprince, you are welcome!!!
Could you please tell a bit more about solving question E with O(n+m) complexity?
If you are interested, in the third spoiler of the problem is a linear solution to it. You can read more about Strongly Connected Components (SCC) here. Another part of the solution is quite easy i think. If I am wrong feel free to ask me.
Wouldn't be complexity for this solution is O(n*m) ?? As you are running two loops:
for (int v = 0; v < n; ++v) { for (auto to : g[v]) { if (comp[v] != comp[to]) { cg[comp[v]].push_back(comp[to]); ++indeg[comp[to]]; } } }
At worst case wouldn't it be O(n*m) ?
No, it will not, because of we will iterate over each vertex and each edge of the given graph only once in this two cycles. So the complexity is O(n + m).
In problem E, could anyone show that the solution, explained in second para of the tutorial, will always give an optimal answer.
If the number of edges added is less than the number of vertices with indegree 0 in the graph's condensation ( other than the vertex containing the capital), then we will still have a vertex in the condensation with indegree 0 and which does not contain the capital. This vertex is unreachable.
On the other hand, if you add all edges from the capital to such vertices, we can show that any vertex in the condensation is reachable; just "backtrack". Say if you want to reach a vertex u in the condensation, find a vertex v1 such that v1-> u is an edge. Then find v2 such that v2->v1 is an edge. We must terminate somewhere because the graph is a DAG. It can terminate only at a vertex with indegree 0, and this vertex is the vertex containing the capital.
In problem E , why do we need to again run a dfs according to count? Why does this solution 39525886 gives answer 1 more than the correct answer for the test case no:4? Can someone help me in understanding the incorrectness of my solution? If possible , please explain with a sample graph.
i also have same doubt .if you know the solution let me know
My solution approach for Problem E: First of all , I take topological order of each node. Then, I run DFS from the city and then from the topological order. And answer should number of connected component — 1.
Can someone explain to me how and WHY this dp solution for F works? I really don't understand O(n^2*k^2) for loop, but I don't understand also ans=(1,10^5)∑ i=dp[f[i]][c[i]] part. I think this way: if I let's say use c[i]=2 cards and k is equal to 3. I need to use my 3rd card that is not my favorite but that instantly means that some other card won't have same amount of c[j]. What am I missing?
Formal proof for O(n*m) in E? I have intuitive proof but I want to see mathematically precise proof.
for D i tried a different approach which led to the same min no. of changes...but diff array.. but I think the judge is checking only for a particular array...whereas in the question it says print any array..
my code
No, the minimum changes in testcase 1 is 3 whereas your code outputs 4 which is wrong
I was wondering if there can be a solution for E with DSU
We will count number of Disjoint Unit for ans..?
I think it can work with dsu ,but when we unite them we need dfs too.
like this 39531065
Thanks a lot for nice tutorials:)
Need help for D problem: I am doing the same approach as in editorial but it is giving wrong answer in testcase 8. Please help.
I think the problem is in updating the array. What I am doing is maintaining a pointer p1(representing remainder) which initially starts from free[0]%m and then moves forward in circular fashion. Whenever I see that p1%m has count < k, I change value free[i] such that free[i]%m = p1%m. Please I cannot find my mistake. Need help.
Code
I'm getting a wrong answer on the same test and I applied the approach as in the editorial. did it work out with you?
No man, I couldn't figure it out :(
You can check the possible cause here. Your solution is indeed wrong for the test case I created.
Help needed understanding problem F, thanks
Try to solve this problem first :
Given N persons and M cards, where each person can have atmost K cards, what is the maximum possible value of total joy levels ? The joy level of a person having x cards is H[x].
Example : N = 3 , M = 4 , K = 3
Maximum value of total joy level can be obtained by giving 2 cards to person 1 , 2 cards to person 2 and none to person 3. The ans is 12 (H[2] + H[2] + H[0]) in this case. Note that there exists other possible distribution of cards such that total joy level is 12. Above is just one way.
Can someone please explain problem F ? Thanks.
A very nice contest. In problem E, my approach is the following: I used the concept of Disjoint Set Union. I say 1. whenever (in the input) vertex v (as input) is the capital. OR 2. the root of vertex v (as input) is the capital I don't perform union operation. The answer are the number of vertices whose: root(vertex)==vertex && vertex!=capital
The approach works fine for the sample test cases, I got wrong answer in 4th test case. Please provide some small test cases to try my approach on.
Your program fails on this test case.
0
1
Good luck :)
Tank UU I found the Bug
For problem E, I got AC by pretty simple implementation, without taking reverse graph, without counting in degree: 39539472
Is my solution correct or the test is weak? Is there any case when my solution will fail ?
My approach is:
1. Mark all the nodes which are reachable from s
2. Run dfs in the original graph and push the nodes in stack according to dfs finishing time.
3. Pop each node from stack and if it is still unvisited run a dfs from here and increase answer by 1.
vovuh, can you please take a look ?
Your approach is also correct, I have the same idea as yours and BledDest has proved this solution correctness
Thanks for your reply. What's the proof of the correctness of such solution?
In this post adding a vertex means adding a directed edge from s to this vertex.
Suppose that your solution adds some vertex x to the answer and it is a bad move (in the optimal answer you should add some other vertex y such that x is reachable from y). Then there are two cases:
1) y is reachable from x. Then x and y belong to the same SCC, and any vertex that is reachable from x is also reachable from y (and vice versa). So there is no difference between adding x and adding y.
2) y is not reachable from x. Then since you pushed vertices to the stack according to their dfs finishing time, then y will be pushed later than x, and extracted before x. So the solution won't add x to the answer but will instead add y.
Is the proof clear?
Could you please explain with an example?
But what if the graph is:
n = 3 m = 3
1 -> 2
2 -> 1
1 -> 3
And suppose we are starting our DFS from 1. Ideally node 3(x) should be pushed into the stack before node 2(y). But here it is possible that 3 is pushed after 2. Am is missing something here?
Edit: Found my mistake!
for the problem E why do we need to sort the array which stores the cnt?
Sorting is required because we have to connect the components of the graph greedily!So we need to find the source with maximum connected nodes!
To find the source from which maximum nodes can be reached. This is important because we have to connect the graph greedily!
Isn't it possible that the nodes in sorted order may visit the similar nodes ?
Yes it is .That's why after sorting the nodes we have to run the DFS and convert all the bad nodes into good ones.
What i was asking is let's say if node 1 in sorted order visit 4,5,6 and node 2 visits 5,6,7 and node 3 visits 2, 7. Then the 2nd node will be selected while it is not required. Am i missing something ?
Node 2 won't be selected because according to your example node 3 visits node 2 that means you will run DFS from node 3 before node 2 . DFS from node 3 will convert bad node 2 into good node hence avoid revisit .
for (auto it : val) { if (!ok[it.second]) { ++ans; dfs1(it.second); } } In sorted list, node 2 will come before node 3 as its count is 3. Can you plz explain how node 3 is selected before node 2 ? "according to your example node 3 visits node 2 that mean you will run DFS from node 3 before node 2". How ? I hope you are considering all 1, 2 and 3 as bad nodes.
You need to sort node according to the amount of node you can visit from that node ..in non increasing order In your example we can reach 4 nodes from node 3 but only 3 nodes from node 2 .That means 3 will come before 2.
Oh My bad.I got it. Thanks Buddy.
Yeah :)
What is Greedily? And what happens if we don't sort? (I think I understand, but cant delete this message)
Cool!
Hello, Could someone tell me what is the formal proof that the solution of problem D is optimal? I know someone has already written some proof but I really can't understand that one. Thanks,
My solution for problem E is as follows:
Time Complexity: Linear
Solution
would anyone provide better explanation for F . ps: provide recursive solution if possible
http://codeforces.com/contest/999/submission/39534469
In E problem is that correct? Count SCC number with 0 indegree and substract 1 from answear if S lies in SCC with 0 indegree?
Yes that works ... informally, when you connect a vertex to an SCC with in-degree 0 (let's call it C), you will be able to reach the maximum number of nodes, because the rest (unreachable from C) is completely disconnected from this SCC, so you'd have to add a new edge anyway, and if you choose to add an edge to an SCC reacahble from C, you won't reach C itself (if you find SCC so that none is a sub-graph of the other, e.g. with Kosaraju's algorithm), and will still have to add a new edge, which will make the previous one redundant.
Could somebody please point out to me why I get WA on this solution for 999D - Equalize the Remainders ? 39544753
Hi! Your programs fails for example on this test case.
6 6
3 5 3 5 2 8
Right answer:
7
4 7 5 6 2 9
I hope it will help you, good luck :)
Hey! Thanks for your time. I think I fixed this bug by not reversing the 'free' vector, but it still give me WA on test 8. I'm not sure if it actually got fixed for all the cases I don't quite understand the basis on which we find the closest element to increment(I don't understand why the editorial chose to do the adding and removing in the same loop instead of doing it in 2 loops. How does that make the solution optimal?). Here's the submission 39604949
You can check the possible cause here. Your solution is indeed wrong for the test case I created.
http://codeforces.com/contest/999/submission/39629449 I think the main idea is the same with the editorial.
But I can't understand why my code is incorrect on test case #8. Iterating 10 times output is different from iterating twice.
Would anyone explain why two output is different and my code is wrong. I'm sorry for my bad English.
I solved it. Thank you. (i--;)'s locations was reversed.
Can anyone please tell me what is wrong with my logic or implementation for problem E? what I am actually doing is- 1> dfs(capital) and mark all visited nodes as good. 2> now run a bfs(bad-nodes) and put them in priority_queue({degree,node}) 3> take nodes from priority_queue from top and run dfs(node) only if it is bad. here is my implementation
Your mistake is in bfs function
I fixed your code but it gave TLE on test 11. This is the code 39669926.
thanks! But i think worst case time of my code is ~10^7 i.e n(n+m) + nlog(n) ~ n^2. can you please explain why i am getting TLE
You are welcome! I fixed your code so it gets AC now(39677394). There are 3 main reasons why your code worked slowly.
1)In your bfs function you had
map<int,bool> v;. I changed it tobool v[5005];. map works in logarithmic time. Array works in O(1). Never use map, if you can use a simple array.2)Never use long long type if you don't need to. long long works slower than int.
3)iostream works slowly. Use stdio.
For problem C i got this error. Can anyone tell me how to fix it? I'm stuck
This is the error:
wrong answer Unexpected EOF in the participants output
This is my submission: http://codeforces.com/contest/999/submission/39488231
You have used variable
tempwithout initialization. You have to add this line to your code.But your solution is too slow(it gets TLE on test 4).
In problem E, linear solution, what is the purpose of dfs3() ? In order to avoid source vertex containing SCC having indegree 0, just do indegree [comp[s]] = 1.
I have implemented top down approach for 999F,please have a look at my code and tell me where am i going wrong,as i am facing problem in clearing test case 3 http://codeforces.com/contest/999/submission/39853333
why WA https://codeforces.com/contest/999/submission/55944188 problem D
You can check the possible cause here. Your solution is indeed wrong for the test case I created.
My alternate solution to E: 1. Generate topological ordering on the graph, first calling dfs on s 3. for vertex v in topo: if (!reached[v]) ans++; dfs(v)(updating reached instead of explored); 4. Print ans
In 999E - Reachability from the Capital after we add an edge to a bad vertex shouldn't we be finding the order of bad vertices again. Can someone help me understand how the same order of bad vertices work even after adding an edge?
It is true that cnt of vertices reachable from other vertices does effect the after adding edge from src to Max Reachablitiy vertex.
we dont care about cnt of reachable vertices.we dont even care about order.
It is similar to deleting largest subtree from graph recursively. May be No of times you delete largest subtree doesn't change.? I'm not sure what observation intended solution is using ? How is it even working ?
in problem 999E - Reachability from the Capital: i did a DfS from the capital to connect the good cities and for each bad city i started a DFS and if it reaches a new node or a node marked with 2 it changes it to 1 and when the DFS ends i mark it with 2 and the answer is the number of 2s but it is not running 63881015 can you please explain why it isn't working
In Question E, my solution is giving MLE. Could anyone please help me. Link to submission : https://codeforces.com/contest/999/submission/66542471
I have an extremely easy solution for problem E with only one very small dfs in O(n) and have a look at my code .. We can also prove its correctness.
https://codeforces.com/contest/999/submission/90504569
My solution for problem E is: Using Tarjan's algorithm to find the graph's strongly connected components and change it to a DAG. Then you will find the answer is the number of points with no in degree. In particular, if in[s]==0, answer--.
This is for everyone who doesn't pass TC 8 for 999D - Equalize the Remainders.
If you solve this without binary search and keep two pointers for remainders under $$$\frac{n}{m}$$$ and for those over it, check if you update the pointers accordingly.
My solution with a bug: 152495726 and here's my solution without a bug: 152500977.
A simpler test case than TC 8, which I thought of, that also points out the bug:
Y'all's solutions usually print 9 as the answer, but the correct answer is 4.
Nice E question. "It can be proven statement" can be added in question statement itself since it was proved in editorial.
I learned a lot from the proof but I think this problem should be in Div4 since the proof is easy and need no explanation.