I’ve though about this for a couple hours but I’m unable to make much headway. It goes like this :
You have an array of size n and q queries. Each query is of the form (l, r, k). The answer to each query is the index (1-based) of the leftmost number in the range [l, r] which is greater than or equal to k. If there is no such value, return -1. Constraints: n, q <= 1e5, l <= r and the elements can be from 0 to 1e9. The program should run within a second.
Example input :
n = 5, q = 2
7 4 6 9
Queries :
3 4 7
2 4 5
Output:
4
3
I feel like a maximum segment tree might work here, but I am unable to put it together. Please help. Obviously, a O(n^2) solution would not run in time. I think the intended solution is O(nlogn).










Binary search on the position of this element, using an RMQ structure to check if RMQ(l, x) ≥ k.
Please explain further. Also, isn’t that O(logn)^2 per query? (The intended solution is O(logn) per query)
You can do the RMQ part using a sparse table and reduce the complexity from O(lgn) to O(1) per RMQ. Then its O(lgn) per query due to binary search.
A maximum segment tree will work.
If max[l, r] < k, obviously there's no such element in the range. If not, with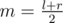 , either max[l, m] or max[m+1, r] is greater than k. Since you want the index found to be as small as possible, whenever max[l, m] >= k, recurse left. If not, recurse right.
, either max[l, m] or max[m+1, r] is greater than k. Since you want the index found to be as small as possible, whenever max[l, m] >= k, recurse left. If not, recurse right.
This is easily done in O((logn)2) per query, which should be sufficient — one log to get to the index, the other to query the segment tree for a range.
It should also be possible to modify the segment tree to build the searching into the query, and get each query done in O(logn), but it's highly likely you won't need that.
Here is another way to solve this in offline.
Sort all the queries according to k in decreasing order, also sort all the numbers in the array in decreasing order and keep them somewhere else.
Now when processing a query (l, r, k) go through the sorted list of the array and mark all the indexes i such that ai ≥ k. This way all the numbers that are ≥ k are marked when a query is processed. Now the query becomes find the leftmost marked position in the segment [l, r] which can be solved easily using a segment tree. Final complexity would be O(nlgn)
It can be solved by using set. Querys would be stored in set and sorted by K. Just go trough array and if some query starts at position i insert it in set. And for every a[i] we do binary search in set, and answer for every query thats grater than a[i], and also erase them.