Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | SecondThread | 148 |
| 7 | atcoder_official | 147 |
| 7 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
| Name |
|---|



Thank you all for the nice problem set!
I'm not sure what is the complexity of your solution for D, but it can be solved it O(t).
Can you please explain your solution?
Build a frequency array for the values given in input. Run BFS at (0, 0) and decrease the frequency of the current distance, if the frequency of the distance is -1, this means one of the four walls (borders) must be determined now. So undo the last level of BFS, try to block one of the remaining walls, and continue with the simulation. If the four walls are determined and the size of the grid is t, we have a solution.
You can try all permutations of {"left", "right", "top", "bottom"} to specify the order in which the walls will be determined. However, since we can skip permutations that will produce rotated or flipped grids, we only need to try the following three permutations:
left, right, top, bottom.
left, top, right, bottom.
left, top, bottom, right.
Complexity: O(3t).
In fact, arsijo's solution can also be O(t). Only paris (n, m) that satisfy nm = t and that |(n - x)| + |(m - y)| = b need to be calculated.
Additionaly, we can assume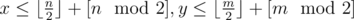 , then there is only one pair (n, m) which satisfies the contidions.
, then there is only one pair (n, m) which satisfies the contidions.
Can you please explain why there is only one pair (n, m) which satisfies these conditions?
Problem B is just that?
Note that if you want to maximize the product of two numbers a × b with a + b = n, you need the maximize the minimum of them. So the maximum product is when a = b or |a - b| = 1 (if n is odd).
How can we achieve this for all segments? If the content of all segments was alternating, the difference between the number of ones and the number of zeros will be 0 if the length of the segment is even, otherwise it will be 1.
Hasan , can you explain it with an example please ?
Sure, let n be 6 and our output be 010101:
For segment "1 4": the length of the segment is 4, the maximum product we can get is 2*2, as the string is alternating, the number of zeros and ones will be the same (2) in the substring [1, 4].
For segment "2 6": the length is 5, the maximum product is 2*3 or 3*2, and any alternating string of length 5 will have 2 digits of one type and 3 digits of the other type: 01010 or 10101.
So you don't even need to read the segments, an alternating string will get the maximum product for each of the segments!
Hope it's clear now!
For problem D how do you prove that x = the minimum number such that freq[num] != (num<<2) ?
in endless plane for any x > 2 freq[x] = 4 + freq[x - 1]
There is a much shorter (and arguably easier) solution for E.
Let us do a binary search for the answer. Then we have to check, for fixed A, if there is a k-path such that every other vertex is at distance at most A from the path. But if any vertex cannot reach this imagined path, then also some leaf cannot. So, informally, we place a pawn on every leaf, and have all the pawns walk a distance A up a tree, cutting all the vertices that are left behind from the tree. If all that is left is a short path, then A was good enough.
More formally: we prune the leaves one-by-one. As long as the tree is not a path, we seek for a leaf x in a tree with a parent y such that the distance D[x] already covered by x satisfies D[x] + weight(x, y) ≤ A. We then cut x from a tree and increase D[y] to D[x] + weight(x, y), if needed. We repeat it until the tree reduces to a path shorter than k (which means A is good enough, we detect it by keeping track of vertices with degree ≥ 3), or until we run out of leaves that can be pruned, in which case A is too small.
Worked like a charm and makes for a quite short code: 40004166. Either this is good, or the tests missed it :)
I think it's an elegant solution to the problem, but the complexity for this algorithm is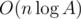 (where A is an upper bound for the answer) instead of O(n). Not a problem since the time limit was wide enough.
(where A is an upper bound for the answer) instead of O(n). Not a problem since the time limit was wide enough.
Yes, obviously :)
This is such a beautiful solution (to me at least). Simple and elegant :)
Thats a really good solution! Would you please tell me how you got the intuition of applying "binary search the answer" in this question since I could not directly prove that if there is a k-path for some "A" then there would always be one for all values greater than "A" — This is what i read somewhere is the basic property of questions that involve binary search the answer.
For this property it is quite easy: Take B > A. If there is a k-path such that every other vertex is at distance at most A, then there also exists a k-path such that every other vertex is at distance at most B -- the very same path.
It gets more subtle with this algorithm: suppose you take some A and apply the algorithm, and the set of remaining vertices is a path of length at most k. If you take B > A, the remaining set must be a subset of the previous one (as all the cut vertices will still be cut), and it must be connected (we only cut the leaves). So it is also a path, not longer but possibly shorter.
"Note, that it is always optimal to use roses in even positions and lilies in odd positions. That is, the string 01010101010 is always optimal"
What is bad in 101010101 ? :D
Nothing. Even 10101010 will be accepted.
arsijo Can you share your code for D ? Also what's the time complexity ?
i am not sure(!), but it is unreal to say the complexity because we haven't enough prime number theorems. Max number of dividers (for numbers<10^6) is 240 for:
720720 = (2^4) * (3^2) * 5 * 7 * 11 * 13;
831600 = (2^4) * (3^3) * (5^2) * 7 * 11;
942480 = (2^4) * (3^2) * 5 * 7 * 11 * 17;
982800 = (2^4) * (3^3) * (5^2) * 7 * 13;
997920 = (2^5) * (3^4) * 5 * 7 * 11;
We check pair (n,m) for O(n*m) = O(t)
So we can say that the worst way complexity is O(120*t)
Yeah, Thanks. Can you tell how to prove that x is the minimum i (i > 0) such that number of occurrences of i in the list is not equal to 4*i ?
Imagine rhomb on endless plane, where number of occurrences of i in the list is equal to 4*i for any i. Now try to cut rectangle n*m clear to the center. Minimum distance from the center to the limits of rectagle is somewhere up-down on vecrtical line or left-rigth on horisontal line. let we have that minimum distance X. Than, there is number X+1 outside rectangle, that break 4*i formula for rectangle. As we start from 0, x = X+1.
Thanks a lot :) Understood
Divisor function is formally subpolynomial, in another words:
So, considering the fact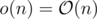 , the complexity of the algorithm is
, the complexity of the algorithm is 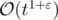 , where ε could be as small as you want.
, where ε could be as small as you want.
But in competitive programming you should give attention to the maximum value of the variable and to the constant that's hidden behind the complexity. So, the finest approximation I've found is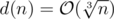 , which gives the final complexity of the task as
, which gives the final complexity of the task as 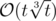 .
.
EDIT n → t in task complexity.
Thank you :)
For problem D, the only thing you are checking is max value and n, m. U also need to check for having 2 0-s, having more than enough appearances of 1, or 2.. etc
The problem statement guarantees to have exactly one 0
What about the other numbers ?
After determining n, m, x and y, you can calculate the matrix and check if the frequency of the numbers is the same as given in the input.
My solution for Problem D:
Let m be the greatest number that has frequency of 4m. Then, the height (i.e. the distance between opposite corners) of the rhombus is 2m + 1. This means that smaller side of the rectangle must be greater or equal to 2m + 1. This can also be used to prune the search space. Another important usage of this fact is that the horizontal or vertical distance from zero-cell to sides can not be smaller than m. The minimum of horizontal and vertical distances to sides can not be greater than m, as we assumed m is the largest rhombus side that fits in the rectangle (*).
Now, because the rectangle is symmetric, we can assume that the zero cell is on the top-left quarter and thus the max number is at the bottom-right cell, and row <= column. Let b be the maximum of the numbers. Then the potential locations for zero-cell is the line r + c = n + m - b. Out of those points (r, c), using (*), we can see that it's sufficient to check just two points, one with row equals to m, and the one with column equals to m.
Code
I just happened to print 0101... But printing 1010.. would have been okay too right?
No one is stopping you from submitting again
a*b=b*a so it is ok
Solution for E:
Just try to prove that some segment of diameter of length less than or equal to k would be the optimal answer. First, try to prove for a more particular case, k=n.
Implementation details: http://codeforces.com/contest/1004/submission/40027676
Can anyone tell me what is wrong with this submission? http://codeforces.com/contest/1004/submission/40022548
h is always smaller than w in your code. In fact, you don't check every pair (n, m).
In problem D "If we know n,m,x, and b" But, why you know b?
Because we are assuming that b is the maximum distance to a corner cell, which is equal to the maximum number in the list.
Thanks a lot.
Problem E can be solved in N * log(C) time without hard math :)
Do binary search on the answer, let d be the value we have to check.
Let 0 vertex be the root of the tree. Call vertex 'sad' if it needs a "chosen" vertex in its subtree (back_edge_length + max_distance_to_vertex_in_subtree > d).
'Sad' vertexes form a subtree of our tree. Call vertex a 'sad kid' if it is a sad vertex without sad chldren.
If there are > 2 sad kids, one path can't go into all of their subtrees, binary search answer is NO.
If there are exactly 2 sad kids, its easy to see that answer is YES <=> path between this two kids fits (length < k and distance to each vertex <= d).
If there is only 1 sad kid, answer is YES <=> the path from the kid to the root (but not longer than k) fits (distance to each vertex <= d).
If there are no sad kids, answer is YES (you can choose root alone).
So, binary search checking can be done in O(n): find sad kids with dfs; check paths for distance to vertexes with bfs; find path between two vertexes with dfs.
for F problem: I think we can maintain 2 segment tree. The first one computes the sum-OR.
the second one computes sum of f(i) where i is in range [l,r] and f(i) is the left-most position that the sum-OR of range [i,f(i)] >= x.
With 2 above Segment Tree, we can have a nlog^3(n) solution:
For the second one, it's easy to see that function f is a non-decreasing array. So we find the right-most postion r' that f(r') <= r. And the answer is (r' — l + 1) * (r + 1) — sum(f(i)) where i is in range [l,r'].
I think we can get a nlog^2(n) solution by using a Segment Tree to maintain the position where the sum-OR changes in both 2 directs. I need help for this part. Thank you.
Thanks for reading my comment despite my bad English.
Yes, that's the exact solution I came up with, tried submitting $$$log^3$$$ solution but it TLE'd. Then I did what the part you needed help for, but not exactly how you said:
We can do walking on segment tree technique to get rid of one $$$log$$$ factor. Take a look at the $$$solveOR$$$ function there are comments with extra explanation, code: 180024090
I'm posting this because the editorial is missing and I think this is important part of this solution.
For problem D how to check if matrix is valid in faster than O(t)?
Is there O(1) way?
A particular matrix cannot be checked in O(1).
It takes O(t) to actually read the input, so probably not dude.
When will the editorial for F be released?
I can translate it from russian:
We call the value of the segment — the result of the bitwise OR of all numbers on this segment. We will call a segment good if its value is not less than x .
Let's first solve the problem when we need to respond to a query [1...n] . We will solve the method of divide and conquer. Let's divide our segment into two equal parts: [1..n / 2] and [n / 2 + 1...n] . Then we need to solve the same problem independently for both parts and find the number of good segments that start on the left and end in the right. Let's look at the values of all segments that start on the left side, and end in position n / 2 (we will call this a suffix). The number of different values will be no more than log(MAX Ai) because bits can only be added. Then let's find the last position for all the different values on the suffix, where such a value will be. Also for each value on the prefix, we find the first position with this value. Then we can go over the value on the suffix, the value on the prefix, find the number of segments with such a value (since we know the boundaries on which these values will be retained), and check that the value of their bitwise OR is suitable.
Now let's analyze how to solve a problem with any segments. We need a data structure. Let's build on our array a tree of segments, where each vertex contains: dp1i - the first position where the bit is encountered i on this segment, or n + 1 , if there is not this bit here; dp2i - the last position at which the bit is encountered i on this segment, or 0, if there is not this bit here; dp - the number of good sub-cuts of this segment; Using arrays dp1 and dp2 , we can find all the different suffixes and prefixes. Then when updating the value of one number in the array, we will need to update the whole log(n) vertices in the tree of segments. How do I respond now to requests? Find the necessary vertices in the tree of segments. We take the answer from them. Now the array is broken up into log(n) segments, and we need to find answers for the unions of every two neighboring segments. This we can do as well as when calculating the value dp in the top. This decision will work for O((n + q)⋅log2(MAX Ai)⋅log(n)).
Note that if we go through the suffix in ascending order, the value on the prefix will fall. Then we can find the answer for the top for log(MAX Ai) , using two pointers. This decision will work for O((n + q)⋅log(MAX Ai)⋅log(n)).
if this is the intended solution what's the point in making X fixed in all queries ? i thought it might help!
the dp contains the number of good sub-segments of this segment. It depends on x.
Can someone please explain question B, why 010101... or 101010... are optimal solutions. How to deduce this idea from the question ? I get that for every segment of length even , even_no/2 should be the count of lilies and roses and for segments of length odd, no/2 and no/2+1 would be the best. Thanks
If you got an insight of the required no of roses and lilies in both the cases of length of the segments (**The only requirement to solve the problem**,
Consider the alternating case 01010101..., it is clear that if you pic any subsegment of this sequence, the number of 0's and 1's will satisfy the above conditions.
Similarly, it is true for 10101010....
Note: You just need to maximise the sum of product of no of roses and lilies in the segment. Exchanging their numbers won't affect the product. (a*b=b*a)
And in order to deduce it from the question, you just need some good observation skills which will develop over time with lots of practice. So Keep Coding!! :)
It is possible to solve problem E with a greedy algorithm: find the center of the tree (which we know must be part of the path) and run a DFS from it, storing the greatest distance to the root appearing in each node's subtree. Now we can increment the path greedily by storing the greatest distance to the path in each node's subtree in a priority queue, and adding to the path the node with greatest such value. The children of the center node are initially added to the queue, and, whenever we add a node to the path, we add its children to the priority queue. When adding the children of node k to the queue, the greatest distance to the path in their subtree is simply [greatest distance to the root in the subtree] — [distance root->k]. We must also take care to keep the solution as a simple path; this can be done by, when adding node k to the solution, erasing from the priority queue all its siblings (except for when adding a child of the center node, since the center can have 2 of its children on the solution). Complexity is O(N*log N). Code: http://codeforces.com/contest/1004/submission/40096868
Problem D, why we should find the minimum i that the number of occurrences of i in the list is not equal to 4*i?
Notice that if the matrix is infinite in size, there will be 4·k occurrances of the number k in the rhombus:
3
232
32123
3210123
32123
323
3
If the matrix has finite size (n,m), the rhombus will be cut off at some point, and the number of the first rhombus layer that is cut off (has less than 4k occurrences) will be the distance to the nearest edge from (x,y), the coordinates of 0. Since a valid matrix may be arbitrarily reflected/rotated, we can pick an arbitrary edge, e.g. the left edge to be closest to (x,y). In that case, x must be equal to the first number with less than 4k occurrences.
Solution of F,please.I've tried my best but still can't solve it
in this comment
Where's the code???
please help in problem E getting WA on test case 12
?detaR tI sI
Alternate easy solution for problem E:
Root the tree at node 1. Now the optimal path will be either have two ends such that no node in its subtree(except itself) is part of the path (when path is bent at lca of two ends), or it will have only one end(when it is a straight path in which one end is an ancestor of the other).
Binary search on the answer, and each time, do a dfs, and greedily select nodes which have no other nodes selected in their subtrees, and not selecting them would violate that answer.
If greater than 2 nodes are selected, then answer doesn't exist. Otherwise, just build the path between the two selected nodes, and check if the answer is satisfied.
Why is this problem rated 2400 lol