Tutorial is loading...
Problem idea: MikeMirzayanov, awoo; prepared by: vovuh.
Tutorial is loading...
Problem idea: MikeMirzayanov, prepared by: MikeMirzayanov.
Tutorial is loading...
Problem idea: MikeMirzayanov, prepared by: awoo.
Tutorial is loading...
Problem idea: vovuh, MikeMirzayanov; prepared by: awoo.
Tutorial is loading...
Problem idea: Errichto, prepared by: Errichto.
Tutorial is loading...
Problem idea: Lewin, prepared by: Lewin.
Tutorial is loading...
Problem idea: Endagorion, prepared by: Endagorion.











G is really a strong problem.
When I saw G during the contest, I built a network flow graph: For each tree vertex i build a chain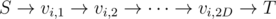 with infinity capacity, D = max{di}; for each tree edge (i, j) link all edge (vi, 2k, vj, 2(k + li, j) - 1), (vj, 2k, vi, 2(k + li, j) - 1) with infinity capacity; for each 1 ≤ i ≤ k set edge (vpi, 2di - 1, vpi, 2di)'s lower bound to fi, the minimum flow is the answer.
with infinity capacity, D = max{di}; for each tree edge (i, j) link all edge (vi, 2k, vj, 2(k + li, j) - 1), (vj, 2k, vi, 2(k + li, j) - 1) with infinity capacity; for each 1 ≤ i ≤ k set edge (vpi, 2di - 1, vpi, 2di)'s lower bound to fi, the minimum flow is the answer.
Transform it into maximum flow: to check if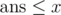 , link (T, S) with capacity x, and create a new source S' and a new sink T', for each 1 ≤ i ≤ k remove edge (vpi, 2di - 1, vpi, 2di)'s lower bound fi and link (S', vpi, 2di), (vpi, 2di - 1, T') with capacity fi. If and only if the maximum flow
, link (T, S) with capacity x, and create a new source S' and a new sink T', for each 1 ≤ i ≤ k remove edge (vpi, 2di - 1, vpi, 2di)'s lower bound fi and link (S', vpi, 2di), (vpi, 2di - 1, T') with capacity fi. If and only if the maximum flow  is
is  , then
, then 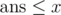 .
.
By using max-flow min-cut theorem, considering cut each chain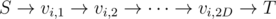 , I transformed this problem into: distribute an integer xv for each vertex v so that for each edge (u, v),
, I transformed this problem into: distribute an integer xv for each vertex v so that for each edge (u, v), 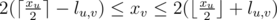 , maximize the sum of fi that satisfies xpi = 2di - 1.
, maximize the sum of fi that satisfies xpi = 2di - 1.
Obviously there is a O(nD) DP, let f(i, j) be the maximum value of subtree if xi = j, which is going to be TLE. I tried to use data structure but still didn't know how to optimize this DP and then contest was ended.
After contest I tried more ways and they failed as well. At last I turned back to think using data structure to maintain DP arrays. The DP array can be discribed as some segments. When transferring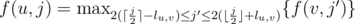 , some segments in f(v, * ) became longer and some became shorter, even disappear. In data structure, we can delete the segment which is earliest to disappear. When transferring f(u, j) = f(v, j) + f(w, j), merge the segments in f(v, * ) and f(w, * ). In data structure, we can do inserting and range adding.
, some segments in f(v, * ) became longer and some became shorter, even disappear. In data structure, we can delete the segment which is earliest to disappear. When transferring f(u, j) = f(v, j) + f(w, j), merge the segments in f(v, * ) and f(w, * ). In data structure, we can do inserting and range adding.
Because of inserting and range adding, I gave up STL set and wrote a splay tree. The code is very long and has lots of details, so I spent 2 days to code and debug. It seems correct to give up G and check A~F during the contest.
Well, it is possible to use only STL data structures to solve the problem.
To do this, one needs to keep the bounds of the segments and the difference of f values between neighboring segments. Also, a trick is needed to account an observation, because it is not a simple addition, it is a max among addition to the previous value and advance operation (and we can't obtain the previous value, since STL set does not support range operations): fnew(t) = max(fold(t) + obs, fold(t - 1), fold(t + 1)). Instead, we should compute how much advance increases our value (i.e. let d = max(fold(t), fold(t - 1), fold(t + 1)) - fold(t)) and then add the difference obs - d to the new value.
You can find my implementation here: 41936437, it is not so long. Also, you can find Lewin's implementation in Java here: 41779819.
Well, it seems to be a good way.
Thanks for the analysis this problems!!!
Doesn't know how to do every xD
O(n * log2(n)) solution of problem F passed with priority_queues and smaller to larger merging in tree. 41932704
I've heard people talking about smaller to larger merging on tree a lot, but I can not find any resources about it. Can you please give me some links which help ? Thanks very much !!!
This blog
Using the seventh set of data, my code is running YES locally, but after the commit it shows that my output is NO.
why ????
http://codeforces.com/contest/1023/submission/41933641
Easier way to solve C: Choose the first k/2 left brackets and the last k/2 right brackets. It's not hard to prove this gives a valid bracket sequence.
How do you prove it?
It is easier to prove because the input string was itself a balanced sequence of brackets.
If you print the input string up to the [k / 2]th left bracket, we know that there has to the matching rights brackets (somewhere ahead in the string) for the still unbalanced left brackets (if any).
So, we just print the remaining number of right brackets until our string's length becomes k.
We don't even need to choose the last right brackets. Just print the given string until k/2 th left bracket, and then remaining with ) s to make the string length = k. 41706259
Thank you very much, man.
Actually, problem D can be easily solved with
O( n + q ). Here you can take a look at the code. The idea is to use 2 pointers, so we can check if the array (except zeros) is correct. How? Initialize array of boolsb[i]which tells us if we can find numberifurther. Then we move right pointerruntila[i - 1] > a[i]. Then we move left pointerlup torand update bools array ifa[l] > a[i]because if we meet numbera[l]further, then the segment should have involved indexi, soa[i]can't be lower thana[l]. So in this caseb[a[l]]becomesfalse.In the end we deal with max number (if it's not in the array, then use one zero to get it. No zeros in this case -> the answer is "No") and finally make all other zeroes like previous or following number, it won't break correct array.
The size of array
b[i]isqand algorithm is linear inn, so time is reallyO( n + q ). Moreover it can be upgraded toamortized O( n )if hash table is used istead of array of boolsTry this input:
My excuses, think I fixed this problem here by taking not
a[i - 1]but last value, which is not 0 (may be so in the beginning). Thank you!I have a really easier solution for problem C: start from the first element and save the number of opening brackets that are not closed in x. the first time that i+x equals to k.(i is the index of current bracket) print the first i elements of s and k closing brackets.
the code for this solution:
I got accepted with this solution :)
the python code :41698479
Could someone help me with problem F?
I don't understand which context "your" was used in in the beginning, what "path" are we looking at... Overall I do not at all understand what the editorial author wanted to say and I can't even "connect dots".
Thanks,
"you" in this context is the same "you" in the problem. Thus, "your edges" corresponds to the edge described by the pairs (gai, gbi).
The "path" spanned by a non-tree edge is the path that connects the two endpoints of this edge that only uses tree edges.
I haven't understood the line "fix the cost of our edges along this path" yet. Does it mean that as we're considering the path from node u to node v on the MST, we'll choose edges from our set (connect Gai and Gbi), which form the path between u and v, then set its cost the same as our considering edge ? Or would you mind giving a simple example to help us understand better ?
Yes, it sounds like your understanding is correct. We can go over the first sample for explanation.
For example, the tree initially has edges 1-2, 3-4, 1-3.
Now, the first considered edge is 2 3 with cost 3, which spans the path 2-1, 1-3. We can fix both of these edges to have cost 3, and also collapse nodes 1,2,3.
The second considered is 3 1 with cost 4. This points to the same (collapsed) node, so we don't need to do anything. Similarly we don't need to do anything for edge 1 2.
Now, for edge 2 4, this spans the path 4-3 (and remember, 3 and 2 are already collapsed into a single node, so we don't need the edge 2-3). We can fix the cost of our edge 4-3 to 8, and collapse node 4 into our previous big node 1,2,3.
At this point, all of our edges are collapsed and we are done (we can still process the remaining competitor edges, but they won't do anything).
As for implementation, you can use dsu to simulate "collapsing" nodes together. You can also do this naively, no need to have any thing like lca or hld. You can see my code for more details: 41725426
Thanks very much, sorry for making you type a lot :P just because the problem is nice and I want an insight into it. You're the best
Thank you for all the extra clarification, I understand the task now :).
In problem F : if I understand it correctly then we need to collapse all the edges on the path of the currently considered opponent edges and for that we need to traverse the path from 'u' to 'v' and you had said "To do this efficiently, we can just do it naively (even without needing to compute LCAs!).". So, can you please explain how can we able to traverse the path without having LCA's??
while (u!=v){ ... if (dep[u]>dep[v]) u=fa[u]; else v=fa[v]; }
thanks!
can someone please explain the impoosible case in prob D. I didn't get that clearly from editorial.
Imagine we have filled some segment with 7s, and there are 9 queries. It is impossible to replace any of the 7s with a number smaller than 7 as all the numbers we can make some element equal to until the end are greater than 7 (in this case, 8 and 9).
This means that if there is some number i such that between the first and last occurrence of i (which must be the left and right segment of the query that made some elements equal to i, since only that query can make elements equal to i), there is a number j < i, we consider the array to be unobtainable (this is the impossible case).
The editorial solution checks whether this is possible by checking the smallest element in the aforementioned range (the RMQ technique) and if it is < i, the array is unobtainable, and if it is not, then there is no earlier query that "interrupts" the ith one.
If there is no earlier query that interrupts any query (from 1 to q), the array is obtainable via a greedy (or some other) strategy.
can we make this output 3 3 3 1 2 YES 3 1 2 please help me
I don't understand what you're asking so I'll cover some cases. Note that it is possible to just change one number in one of the queries.
{3, 3, 3, 1, 2} is possible. You start from all zeroes, make one number equal to one, one number equal to two, and set the rest to three.
{3, 1, 2} is also possible (just make the second number 1, the third two, and the first equal to three).
{3, 3, 3, 1, 2, 3, 1, 2} is not possible as there is a 1 between the first and last occurrence of 3, which is not possible (read my comment above for more clarification).
Of course this is all under the assumption that there were 3 queries. If there were more, then earlier queries overlapped later ones which is impossible, meaning the answer would be "NO" for all of the cases above (if q > 3).
thanks alot
In solution of problem B, when k <= n solution should be (k-1)/2 not k/2. also mn = k — n I believe, not n — k.
Minor typos but probably worth editing :D MikeMirzayanov
I would like to know if we can solve D problem like this....
change any zero value to a non zero value just to its left (or right, doesn't matter), check for occurrence of value "q" in the array, keep track of li and ri as index of first and last appearance of i in array for all possible i and then for every "i" check if there is a value less than i (let that be j) in the array in index range [li, ri] . If such a value exists then we can say that such an array cant occur because query with i>j will always happen after jth query so there can be complete overlap or partial of ith query over jth query and not vice-versa....
I think this a sufficent condition for the solution but i m not able to get ans....
I would to like to know for some flaw in the solution or counter example for the same (explaining the flaw)
Thanks in advance!!!
How will you deal with the time complexity to check if a smaller no. occurs b/w [li,ri] with both li an ri holding equal value.
Also, how are you dealing with a case where 0 can be occupied by q itself and nothing else as q does not appear in that array and only replaced by 0 over there ?
Ans to your first question: segment trees
Ans to your second question: Damn!! that's what is missing ....
I think that is what is missing... I'll solve and get back
Thanks msdcoder7
Bro, any other way to solve other than segment trees ? I haven't used it ever.
I m sry but i m not able to think of any other method.... U can learn it and using that u can find max or sum over a range of indices too ... or u can try to extend it to any other problem which requires range query solving...
You may use fenwick trees. Initialize the fenwick tree array, say
fenwith0s. Keep on updating the tree with1sfor each index of query no.iin the given array for1<=i<=q.To check if a smaller number appears between two ends, say
landr, computediff = fen[r]-fen[l]. Ifdiff > 0, you have a smaller number in between.This is pretty much the idea.
Done Thanks again!!
Lewin
For Problem F, How will u collapse the nodes along the path into larger node without LCA?