Shooting Game
Let PA and PB be the probability of Alice and Bob hitting the target respectively. Then the chances of Alice winning the game are:
which equals 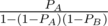 using GP formula. Similarly, for Bob it would be
using GP formula. Similarly, for Bob it would be  .
.
Equating both we get, 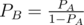 . Return -1 in case you get PB greater than 1.
. Return -1 in case you get PB greater than 1.
SolveForTrisha
Let x be an nth root of unity. Then, xn = 1. So, xn - 1 = 0 has roots 1, α1, α2....αn - 1. We can write this as follows :
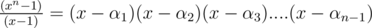
Placing x = 1, - 1 in the above equation and multiplying them, one can get the desired result.
If n is even the expression evaluates to 0 otherwise n.
Polynomial Guess
Consider the polynomial:
Let g(r) be the value of 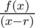 at x = r and y(r) be the given values of the polynomial for r = 0 to 5.
at x = r and y(r) be the given values of the polynomial for r = 0 to 5.
The desired polynomial can be written as :
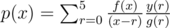
FunctionGame
The main part of the solution here is using the equation : φ(xr) = xr - 1φ(x) , 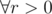 . Rest is just solving GP sums and calculating φ values from 1 to m.
. Rest is just solving GP sums and calculating φ values from 1 to m.
PrimeMaker
Since, the operations allowed are only modifying / deleting a digit and value of n is at max 106, the maximum number that can be formed is of the rage 10n. The idea is to calculate all primes upto 107 and take the minimum number of operations required to convert n to a prime p over all primes p.
Another solution is to observe that we can always get a prime number in the range n - 99 to n + 99 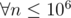 . So, the maximum value of the answer can be 2 only. So, we just need to check whether the answer is 0 or 1. For answer to be 0, n should be prime. For answer to be 1 we have O(10 * d) candidates only where d is the number of digits in decimal representation of n. Each candidate can be checked in O(sqrt(n)).
. So, the maximum value of the answer can be 2 only. So, we just need to check whether the answer is 0 or 1. For answer to be 0, n should be prime. For answer to be 1 we have O(10 * d) candidates only where d is the number of digits in decimal representation of n. Each candidate can be checked in O(sqrt(n)).
CountingTriangles
Let us try to find a series for the number of triangles after n steps. First of all the side length of the triangle after n steps would be m = 2n. Lets iterate over the side length of the triangles that we are going to count currently. Let it be l. Every triangle is either pointing up or pointing down. Lets count them separately and add them in the end. For counting triangles of length l pointing up, we just need to count the number of valid points that can be the topmost point of our triangle. This is equal to 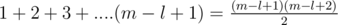 . For counting triangles pointing down, we need to count the valid positions for placing the base of length l. This is equal to
. For counting triangles pointing down, we need to count the valid positions for placing the base of length l. This is equal to 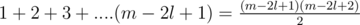 . The final answer would be :
. The final answer would be :
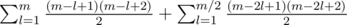 .
. Simplifying and using some series formulas, you can get a formula as :
 .
. If you do not want to solve the series, observe that the final expression would be of order 3 in m. So, instead assume a general 3 degree polynomial, and get its coefficients using base cases already given.
ConfusingTriangle
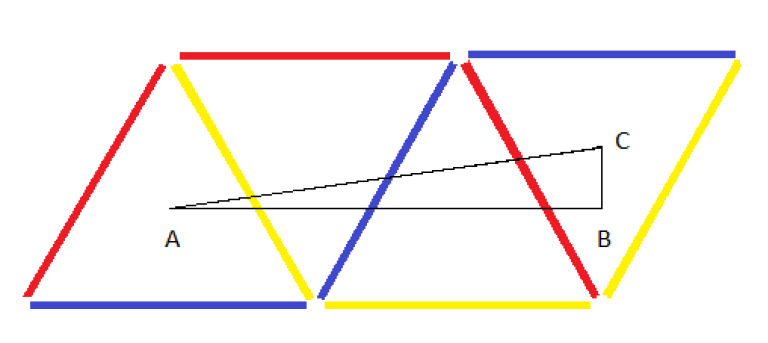
The idea here is to use the mirror property. Imagine that the sides of the triangles have mirrors placed on them. Then the shortest distance between two centroids such that the line between them intersects all the sides exactly once is your answer. Applying pythagoras theorum, the answer comes to be 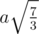
MinimizeExpression
The key to the solution is to use Weighted AM — GM inequality here. Let us write the expression as
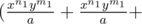 . . . . a times
. . . . a times 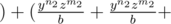 . . . . b times
. . . . b times 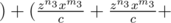 . . . c times )
. . . c times )
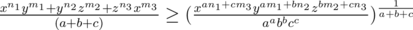
Comparing the RHS of the expression with xAyBzC, solve for a, b and c. The final answer hence would be 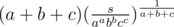 .
.
The conditions given guarantee that a, b and c after solving would be positive.
EquationSolver
The answer to the problem is the coefficient of xc in the expansion of :
where (1 + x + x4 + x9 + .....) represents the choices each variable has.
One solution is to perform binary exponentiation of the polynomial using NTT for polynomial multiplication. The time complexity of such a solution would be O(clog(c)log(n)).
Another solution is to calculate NTT of the polynomial once, exponentiate individual terms to n and then calculate the inverse NTT. Time complexity of the solution would be O(c(log(c) + log(n))).
Tribonacci
T(n) = Mn where M is the given matrix.
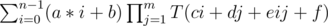
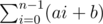
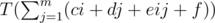
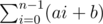
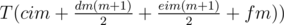
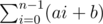

Let 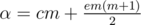 and
and 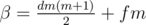 .
.
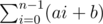 T(αi + β)
T(αi + β)
Let R(n) = T(α)n
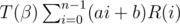
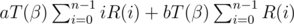
The main part of the solution is to calculate 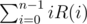 and
and  .
.
Consider the following matrix P(A)
\begin{bmatrix} A & I \\ O & I \end{bmatrix} The matrices P2, P3 . . . are as follows :
\begin{bmatrix} A^{2} & A+I \\ O & I \end{bmatrix}
\begin{bmatrix} A^{3} & A^{2}+A+I \\ O & I \end{bmatrix} Observe that the 2nd element of the first row is the GP sum of matrix A. Therefore, 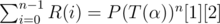
Now, consider 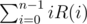 .
.

The first part of which we already know. For second part, Consider 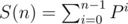
The matrices S(2), S(3) . . . are as follows :
\begin{bmatrix} A^{2} & A+2I \\ O & I \end{bmatrix}
\begin{bmatrix} A^{3} & A^{2}+2A+3I \\ O & I \end{bmatrix} Observe that the second element of the first row is nothing but the desired part. S(n) can also be calculated in the same way the GP sum was calculated as it is nothing but another GP in P. The overall time complexity of the solution is O(k3(log(n) + log(m))).
Also observe that the modulus is 231, so no need to take modulus. We can let the operations overflow. In the end we just add 231 if result comes out to be negative.
Another method of taking modulus is to take bitwise AND of the intermediate calculations with 231 - 1. Both of them are much faster than the modulo operation.










Auto comment: topic has been updated by hitman623 (previous revision, new revision, compare).
How do you "Comparing the RHS of the expression with ..." in MinimizeExpression?
The goal here is to choose such a, b, c (a, b, c > 0) such that the RHS of the expression in the inequality comes to be a function of xAyBzC. For example : given xy2 = 4, to minimize x + y you write it as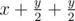 so that you get xy2 on RHS.
so that you get xy2 on RHS.
No, I mean, how to relate the right hand side x^(an1+cm3).. with x^ay^bz^c=s? Or to put it the other way, why should we assume that is s?
Comparing them, you get the following :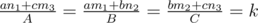 .
.
You are free to choose any k > 0 and solve for a, b, c. The answer is same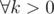 .
.
how to upsolve ? can you move them to practice
I have contacted hmehta. I'll let you know as soon as he replies.
The match is up in the practice rooms.
You will find it in SRMs Category under practice rooms as shown below in the image! :)
Setup Topcoder Java Applet: topcodr.co/SRMGuide
There is something wrong in problem EquationSolver.
The standard solution is based on "calculate NTT of the polynomial once, exponentiate individual terms to n and then calculate the inverse NTT." which is wrong.
Because NTT does the Circular convolution.When you do this process NTT with length $$$2^i$$$,the result polynomial $$$F$$$ is not the answer. If we claim the correct polynomial as $$$G$$$.And $$$F$$$ will be $$$(G \bmod x^{2^i})$$$.
If you want to make it correct,you should do NTT with length $$$2^k$$$ which satisfies $$$2^k>n\times c$$$.But it's impossible with $$$998244353$$$ and time limit.
The correct algorithm is just do the ln transform,and multiply each terms with constant c,then do the exp transform.This works in $$$O(n\log n)$$$.For more details,please check this.