Hello Codeforces!
I would like to invite you to Manthan, Codefest'19, which will take place on Sunday, August 25, 2019 at 8:05 PM IST. This is a combined Div. 1 + Div. 2 round and is rated for participants from both divisions.
The Department of Computer Science and Engineering, IIT (BHU) is conducting Codefest from 23rd August — 25th August. Manthan, the algorithmic programming contest under the banner of Codefest, is being held as a special Codeforces round. The round follows regular Codeforces rules.

All problems in this round were created and prepared by drastogi21, _shanky, Enigma27, _hiccup, KAN and me (hitman623).
A lot of thanks to KAN, 300iq, vintage_Vlad_Makeev, _overrated_, Rox for the testing and valuable comments, and to MikeMirzayanov for the awesome Codeforces and Polygon platforms!
Prizes -
1st place — INR 25,000
2nd place — INR 18,000
3rd place — INR 12,000
1st place in India — INR 6,000
1st place in IIT(BHU) — INR 3,000
1st place among freshers (1st/2nd Year) of IIT(BHU) — INR 1,000
Codeforces T-shirts to the participants who will be the first to solve each problem.
Participants will be offered 8 problems and 2 hours to solve them. As usual, the scoring distribution will be announced later.
Hope you guys enjoy the contest! See you on the leaderboard!
UPD: The scoring is 500 — 1000 — 1500 — 2000 — 2250 — 2500 — 3000 — 3750
UPD: The contest has ended. Congratulations to the winners.
1. tourist
2. Um_nik
3. jqdai0815
First place in India: cerberus97
Following are the participants who were the first to solve each problem and have won a Codeforces T-shirt. Congrats!
A. IgorI
B. Geothermal
C. icecuber
D. ILoLy
E. nocriz
F. GoGooLi
G. jqdai0815
H. tourist
UPD: We decided to give the 8th T-shirt to IgorI for problem A. Congrats!
The editorial has been published.
Hope to see you next year!









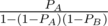 using GP formula. Similarly, for Bob it would be
using GP formula. Similarly, for Bob it would be  .
.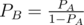 . Return -1 in case you get
. Return -1 in case you get 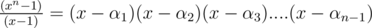
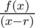 at
at 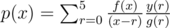
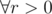 . Rest is just solving GP sums and calculating
. Rest is just solving GP sums and calculating 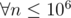 . So, the maximum value of the answer can be 2 only. So, we just need to check whether the answer is
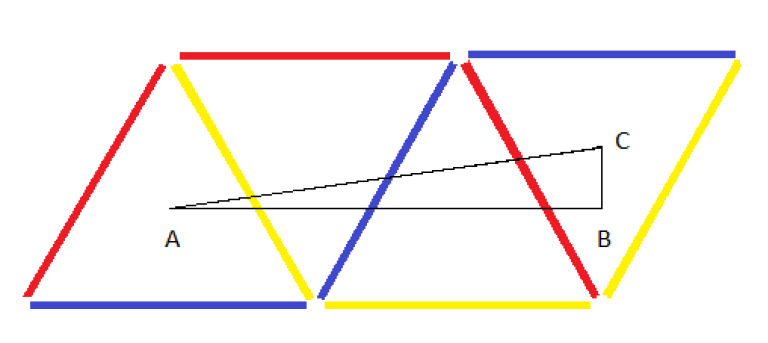
. So, the maximum value of the answer can be 2 only. So, we just need to check whether the answer is 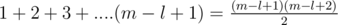 . For counting triangles pointing down, we need to count the valid positions for placing the base of length
. For counting triangles pointing down, we need to count the valid positions for placing the base of length 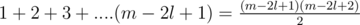 . The final answer would be :
. The final answer would be : 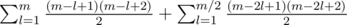 .
.  .
. 
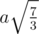
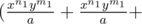 . . . .
. . . . 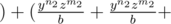 . . . .
. . . . 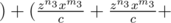 . . .
. . . 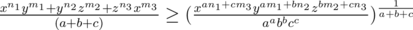
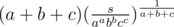 .
. 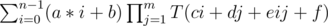
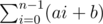
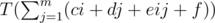
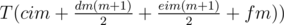

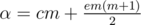 and
and 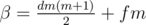 .
. 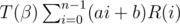
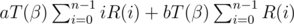
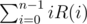 and
and  .
.