cdkrot's blog

Codeforces Round #507 (based on Olympiad of Metropolises) — Editorial
By cdkrot, history, 6 years ago, In English

Div2A ("Palindrome Dance") was authored by jury members altogether, development: darnley

Div2B ("Skewers") was authored by jury members altogether, development: GlebsHP, Codeforces hardened version: KAN.

Div1A ("Timetable") was authored by Zlobober and meshanya, development: kraskevich.

Div1B ("Subway Pursuit") was authored by V--o_o--V, development: wrg0ababd

Div1C ("Network Safety") was authored by V--o_o--V, development: achulkov2.

Div1D ("You Are Given a Tree") was authored by GlebsHP, development and codeforces edition cdkrot, faster model solution: V--o_o--V.

Div1E ("Summer Oenothera Exhibition") was authored by Zlobober, development by malcolm.

Some editorials are being published, please wait a bit :)

Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
  • Vote: I like it
  • +16
  • Vote: I do not like it

Comments Comments (34)
| Write comment?
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I get a Wrong Answer on 1039B. I submit the same code again. I get AC ???

how bad luck...

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

It's a hard contest :(

→ Reply
»
6 years ago, # |
  Vote: I like it +16 Vote: I do not like it

This round made me decide not to used rand() again :(

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it -8 Vote: I do not like it

May I ask whether an O(n log^3(n)) solution of Div. 1 D will get Accepted? (DP + Union by size, O(n/k * log^3(n/k)) for each k)

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What is the proof that We will always be able to get answer in 4500 steps.. I was stuck there for 1:30 hours, I was able to get solution described in editorial.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    The initial binary search will take at most 100 steps.

    Let's say you perform binary search until the interval is  ≤ 50, and then guess random numbers. After a guess, the interval is at most 70, so after two binary search iterations you are again at a interval  ≤ 50.

    Therefore you will have around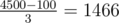 guesses, each one in a interval  ≤ 50.

    The probability of guessing at least once correct is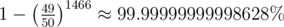

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Then can you please explain me, why this solution is not passing testcases if probablity is this much high. https://codeforces.com/contest/1040/submission/42542608

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +12 Vote: I do not like it

        In the following piece of code, you ask two queries, but only increase the intervals by k once. Should be a simple else, not else if.

         if (get(in, out, low, mid)) {
     high = Math.min(n, mid + k);
     low = Math.max(0, low - k);
} else if (get(in, out, mid, high)) {
     low = Math.max(0, mid - k);
     high = Math.min(n, high + k);
}

        Also I recommend setting a bigger interval limit than 4*k, otherwise you need a lot more time for binary searches. E.g. if k = 10, then in the worst case you have an interval of length 60 after asking, then 50 after one BS iteration, 45 after the second, 43 after the third, ... So you might only get to ask  < 500 questions this way.

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          OK bro. Got that, Trying to remove TLE in 7th testcase by setting a good seed. Thank you!!!

          → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Jakube why u have divided the no of guesses by 3? i ain't able to get this.

      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        After a wrong guess in the interval of size <= 50, the interval will increase on each side by k. In the worst case it will have size 70. However you don't want the interval to grow (because then the probability of guessing correctly will get worse and worse).

        Therefore you do two binary search iterations. In the first one you will get from size <= 70 to 35 + 2*k <= 35 + 20 = 55. And in the second iteration from <= 55 to <= 23 + 2*k <= 23 + 20 = 43.

        So for each guess, you need two additional interactions to guarantee that the interval is again <= 50. For each guess you need 3 iterations, therefore division by 3.

        → Reply
»
6 years ago, # |
  Vote: I like it +99 Vote: I do not like it

I like how Div1A is the only problem without an editorial :)

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +16 Vote: I do not like it

    Finished with it, sorry for the delay :)

    Well, most editorials were written by their developers, with two editorials missing. So yesterday I was very sleepy and managed to write only one of it. But now it is done!.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In Div1D, how exactly do you find the transitions that add new paths from the segment tree efficiently? Knowing the longest incomplete path in a segment doesn't necessarily tell you whether any element of the segment has a longest incomplete path that is now long enough to be a complete path.

I also thought of having each segment hold the minimum extra needed to complete a path, but that can't be updated in O(log n) when merging.

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +3 Vote: I do not like it

    When you process a light child, you can check that the current longest path + a path in the light child is at least k. And then you can check all numbers >= k (you can do it with segment tree on maximum containing length — k, and then find all numbers bigger than zero), and find that path.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I know in Div2D were some problems with rand() Could you please explain what type of random function should we use to avoid these problems??

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +15 Vote: I do not like it

    Check the recent posts by neal, like this and this.

    I pretty much agree with everything he suggests.

    → Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it +22 Vote: I do not like it

Let me try to explain my solution to Div1A (42525555).

First of all, we have some initial conditions: ai + t ≤ bi.

Now, iterating over x, assume we got xi = k. What can that mean?

First, we need to ensure that i-th bus can't arrive (k+1)th and later. How to do that? The only way I see is to ensure that (k+1)-th bus can't arrive k-th — that is, ak + 1 + t > bk.

But that's not all.

If k < i, the answer is instantly No: we can't guarantee that i-th bus will always arrive in first k places (all i — 1 previous buses can always come before i-th one).

If k > i, we need to ensure that i-th bus can really arrive k-th. To do that, we need to ensure that (i+1)th, ..., k-th buses can all arrive at least one position earlier (that is, (i+1)th one can arrive i-th, ..., k-th one can arrive (k-1)th). Which gives more conditions: ai + 1 + t ≤ bi,  ...,  ak + t ≤ bk - 1.

After collecting all these conditions on bi and taking into account that bi < bi + 1, we can generate a solution (or answer No if for some bi its lower bound exceeds upper bound). We can just store array with upper and lower bounds on bi and update it carefully.

The only algorithmical problem here is to update (k-i) boundaries in case k > i quickly enough. To do that, I created an ordered set of i-s for which condition of form ai + 1 + t ≤ bi has not been applied yet. When I apply this condition, I remove corresponding index from the set. There can't be more than n removals each worth, so the overall complexity of my solution is .

→ Reply
»
6 years ago, # |
  Vote: I like it +18 Vote: I do not like it

Never seen trick like Div1 E before..

→ Reply
»
6 years ago, # |
  Vote: I like it +11 Vote: I do not like it

Is it the editorial for Div2C/Div1A would be even more confusing, and so skipped?

→ Reply
»
6 years ago, # |
  Vote: I like it +43 Vote: I do not like it

I have seen a similar idea about div1 D before, in "Petrozavodsk Winter-2015. Moscow SU Tapirs Contest", problem F.

You can Click here

I tried an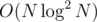 approach but failed at that time, just because it was too complicated.

And my friend who was taking virtual contest with me simply used this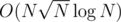 trick, but he failed too :). Maybe N is a little bigger and the time limitation is tighter.

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can someone explain the last part of Div1C where the number of connected components are calculated in linear time

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    For each value, take the edges with that value. Use a DSU data structure to connect the two vertices of each edge. The number of connected components starts at N, and goes down by 1 each time you join.

    The problem here is that resetting the DSU takes O(N) each time, which can be too slow. So modify the DSU to keep track of which vertices you modify. Then, instead of resetting all the vertices, only reset the ones that have been modified in the last DSU.

    → Reply
  • »
    »
    3 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    you can also just do simple DFS, maintaining map<int, vector<int>> adj[N], where $$$adj[v][x]$$$ is the set of vertices adjacent to $$$v$$$, such that $$$c[v] \oplus c[u]=x$$$. Now let's iterate over every vertex, and for each vertex $$$v$$$, and for each color of edge $$$x$$$ adjacent to our vertex $$$v$$$, we do DFS with edges only of color $$$x$$$, starting from $$$v$$$. Easy to see it is $$$O((n+m)LOG)$$$ where $$$LOG$$$ is due to map.

    Link to code: 105101413

    → Reply
»
6 years ago, # |
  Vote: I like it +40 Vote: I do not like it

It's hard to cut off O(n2) solutions, when you propose O(n5 / 3). And you almost did it =) http://codeforces.com/contest/1039/submission/42621125. 4.8s out of 7s TL. The key idea — to process simultaneously every 4 queries. That allows us to use vectorization.

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

why is the test case in 1040 B giving wrong answer

30 Time: 0 ms, memory: 0 KB Verdict: WRONG_ANSWER Input

4 2

Participant's output

1 4

Jury's answer

1 3

Checker comment

wrong answer Skewer 1 remains at initial state.

AND why is Jury's answer correct when we take 1 and flip it then both 2,3 with rotate with it and if we rotate 3 later, then both 1,2 will again flip to their natural position ?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    The output format is 

    1//the number of shifts
3//indexes

    So in your case you take the 4 skewer and the skewers 2, 3, [4] are turned over(but not 1). Jury answer: to take the 3 skewer and the skewers 1, 2, [3], 4 are turned over,

    → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Div 2 E, Compare to Previous Submission

Changed from C++17 to C++14, TLE becomes AC in less than half the allotted time limit...

I'm hecking bamboozled!

→ Reply
»
5 years ago, # |
← Rev. 3   Vote: I like it +3 Vote: I do not like it

Explaining Div2 B or 1040B : Considering L = 2*k + 1, we will have 2 cases :

  1. (n % L) == 0: In this case, we can just consider center points starting from k+1 at intervals of L .

  2. (n % L) != 0 : We notice that there will be two cases i.e( if n%L >= k+1 or n%L < k + 1 ) Notice that n%L tells us the number of points left to cover.

Hence , if n%L >= k+1 we can normally iterate as done in Case 1. (why?) because iterating from left to right we are ensuring that no points in b/w are left untouched also we are sure that moving at intervals of L will not overflow because remaining elements are >= k+1.(think! sample eg 2) .

So what if n%L < k+1 ?? Notice that in former cases the starting point was k+1. To make this case similar to the previous case(n%L >= k+1), we can choose the starting point as 1 ( check the remaining points now will be similar to previous case ). therefore now we just have to iterate the same as former cases but with starting point as 1 !! ( sample eg 1 ) .

My Solution

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

The editorial in Div1D says: "Introudce a dynamic programming on subtree, the dp of the vertex is the number of paths, which can be taken from the subtree and the maximum length of incomplete path, which ends exactly in vertex v."

What exactly does it mean for a path to be complete or incomplete? Are there any constraints on the length of the paths in the way the dp is defined? (it's not clear from the editorial explanation)

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem 1B, Isn't the bound 4k + 2? why is it exactly 4k

→ Reply
»
5 months ago, # |
  Vote: I like it 0 Vote: I do not like it

good tutorial

→ Reply