pabloskimg's blog

smallest K such that number of arrangements of prime factors of K equals N?
By pabloskimg, history, 5 years ago, In English

Basically the title. The problem statement can be found here. No idea how to solve it efficiently.

UPDATE 1: why the downvotes?

UPDATE 2: based on the answers so far, the solution would be to exhaustively explore all combinations of exponents k1, k2, ..., kr (ki ≥ kj for all i < j) such that 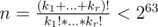and k = 2k1 * 3k2 * 5k3 * 7k4 * 11k5 * ... < 263. During the exhaustive search one can map each n to its minimum k found (for instance, using an unordered_map) and then the queries can be answered in O(1). The problem is: how can you estimate the complexity of the exhaustive search? Any easy way to estimate an upperbound for it?

UPDATE 3: pshishod2645 says there are around 2 * 106 valid combinations of exponents, where did he get that number from?

  • Vote: I like it
  • -24
  • Vote: I do not like it

»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Let the prime factorisation of n be p1n1p2n2....pknk, then we have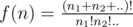 , which means that f(n) doesn't depend on primes but instead on the exponents. So you can find all numbers ( < 263)which are formed by first few primes, Mathematically , you have to find all such numbers such that if the prime factorisation of n contains prime p, then it must contains all primes less than p. The number of such numbers is around 2 * 106, so you preprocess f(n) for all those n and get the answer for all given n in O(1). My code for finding such numbers is in spoliler

Spoiler
→ Reply
  • »
    »
    5 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    "So you can find all numbers (< 2^63) which are formed by first few primes" What do you mean by first few primes? Which are those first few primes?

    "you have to find all such numbers such that if the prime factorisation of n contains prime p, then it must contains all primes less than p" Why do I have to find these numbers?

    Would you mind elaborating your points a little more?

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      The value of f(n) is same for n = 23 * 57, 23 * 57, 313 * 477, so the actual primes doesn't matter but their exponents do, so you have to find all such numbers which contains all primes from 2 to largest prime factor in their factorisation. for example you have to consider n = 23 * 37 but not 23 * 57, because in second 5 is present but 3 is missing.

      → Reply
  • »
    »
    5 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Would you mind explaining how you calculate/estimate that there are around 2 * 106 such numbers? I think knowing how to do this estimation is crucial before one can decide to use this approach.

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I used the code provided in spoiler.

      → Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by pabloskimg (previous revision, new revision, compare).

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by pabloskimg (previous revision, new revision, compare).

→ Reply