Saturday there will be COCI exam in this link: http://hsin.hr/coci/ You can study for the old COCI's here: https://oj.uz/problems/source/122 Also this site has an online judge. The contest will begin at:17.11.2018.14:00 GMT/UTC and it will take three hours.
Please subscribe to the official Codeforces channel in Telegram via the link https://t.me/codeforces_official.
×
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | SecondThread | 148 |
| 5 | atcoder_official | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 9 | TheScrasse | 144 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/23/2024 05:30:08 (j3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Auto comment: topic has been updated by Ahmet.K37 (previous revision, new revision, compare).
Good luck to everyone.
did the registeration begin?
No.
When it will going to begin?
In two days.
Registrations began. you can go to the site with this link: http://hsin.hr/coci/ look at to contest 2
5.00 hours before the exam begins
Thanks dude. I'd miss if I didn't see the topic.
No problem!
Will it take five hours or three hours (same as the previous one)?
it will take 3 hours
Where did your get that information? Here it says three hours and five problems.
Yes
lol so is it 3 or 5?
As far as I know, 3 hours, 5 problems.
thank you
Last 1 hour to the contest
Is the site down ?
Auto comment: topic has been updated by Ahmet.K37 (previous revision, new revision, compare).
How to solve second? I solved the third but not that one.
Thank you, I got the idea.
How to solve the third?
Main idea: We find the answer by counting the number of the ranges for each bit. For that, root tree at one and calculate top to bottom xor's. Now, traverse the tree and you can count the number of the ranges by counting {(0,0) and (1,1)} or {(0,1) and (0,1)} pairs.
Code: https://pastebin.com/Sr9EskiG
UPD: I got AC.
We keep 2 arrays, row[] and column[] which store 2 values; 1 if someone at some point has seen a square that was blocked and -1 if nobody saw it just yet. First we go from left side through all rows, if input at the current row is -1 we set row[current_row] to -1 and continue, otherwise we set both row[current_row] and column[input] to 1. Then we continue to other three sides and we will have 2 cases: 1. if input is -1 then we ask if someone before has seen a value in that row/column before (i.e if element in array row/column is 1), if someone did see it then we print "NE", otherwise continue 2. if input is 1 then we ask if someone before hasnt seen a value in that row/column before (i.e if element in array row/column is -1), if someone didnt see it then we print "NE", otherwise continue
Code: https://pastebin.com/KNqzESdU
See also Noam's notes below.
We iterate over the row number/column number. Consider the i-th value in the L array, Li. Since the first Li fields in row i must be empty, we must have that Uj ≠ i - 1 and Dj ≠ N - i for all 1 ≤ j ≤ Li. Also the (Li + 1)th field in this row must be a blocked so ULi + 1 ≤ i - 1 and DLi + 1 ≤ N - i since otherwise this blocked area would have to be empty. Both of these conditions can be checked in O(1) by pre-constructing various arrays.
Then just do this for U, R and D.
When standings will be avaliable?
Commonly within an hour
Results are out!
Link for the lazy: https://evaluator.hsin.hr/results.php
Brief solutions/hints for the problems (except A because there's no reason to):
For both rows and columns, you get 2 ends X, Y such that before X and after Y there must be white, X and Y must be black and between them it's unknown.
For each row find these endpoints, and then iterate over all columns and check whether some cell that needs to be black according to a column, has to be white according to a row (this can be checked in constant time). After all these checks, swap between the rows and columns and check again.
Hint: solve separatedly for each bit (so each node has a value 0 or 1). You can solve it using a dfs run on the tree.
If K is large enough, then at some point you will jump between 2 adjacent cells. K should be at least (approximately)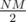 . If K is smaller than twice this limit, you solve by doing dp in
. If K is smaller than twice this limit, you solve by doing dp in 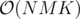 . Otherwise you solve upto the limit, and find the best pair of points you should jump between (It's probably one with the maximal sum but there's no need to solve further).
. Otherwise you solve upto the limit, and find the best pair of points you should jump between (It's probably one with the maximal sum but there's no need to solve further).
Brief explanation/hint of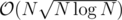 :
:
We first reverse the order of rectangles (and also do coordinate compression). A rectangle is good now, if none of the previous rectangles took any space of the current rectangle. We split the rectangles to blocks of size K, within each block we check all pairs of rectangles for intersections in (total). For each block we also compare it with all previous blocks in
(total). For each block we also compare it with all previous blocks in 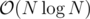 (per block) using sweepline and a segtree: past rectangles represent updates, current rectangles represent queries. The (lazy)segtree I made supports setting each value V in a range to max(V, C) for some constant C, and range query for max.
(per block) using sweepline and a segtree: past rectangles represent updates, current rectangles represent queries. The (lazy)segtree I made supports setting each value V in a range to max(V, C) for some constant C, and range query for max.
K should be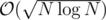 .
.
Edit: Looking at the results, I think my solution to D takes a little too much time. Can anybody else explain their solution? Also for E I'm not sure if my solution can pass in time, I didn't submit it, will check soon.
Edit2: This solution for E recieves TLE on the last 2 testcases when K is 1000, but it passes with 1500. Anyway, did anybody have a better solution?
I spent last couple of hours trying to solve D.
I'm not quite sure I understand some of your points.
Do you mean that, if K < NM then we run the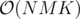 DP?
DP?
I also thought about this, but don't know how to prove it. Do you have some insights?
This is the part I am most confused about. Let's say we pick some pair of adjacent cells (x1, y1) and (x2, y2). How do we choose the number of times we'll jump between them and the lengths of the paths from (A, B) to (x1, y1) and from (x2, y2) to (A, B)?
I was thinking about choosing some lengths k1 and k2, then using DP to find f(k1, x1, y1) — maximum weight of the path from (A, B) to (x1, y1) using k1 steps, same with f(k2, x2, y2). So we are left with K - k1 - k2 jumps that we can do between (x1, y1) and (x2, y2). But what are the limits on k1 and k2 in this case? If we choose some L as the limit (i.e. k1, k2 ≤ L), then the complexity will be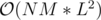 , so L cannot be very big. But choosing small L will lead to nonoptimal answer.
, so L cannot be very big. But choosing small L will lead to nonoptimal answer.
Here's what finally worked for me:
If we assume that when K is large, we'll be jumping between two cells at some point. Then after some k steps, where k < K, the weight of the optimal path will be increasing by the same amount each 2 steps. In other words for some large enough k, it should be true that
So we can use this difference for the rest K - k steps and the result will look something like
But how do we choose large enough k? I don't know :) Maybe someone can help with this?
Here are some values that I tried: