Hmm.. Am I the only one not appearing in the scoreboard?!?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/27/2024 02:25:08 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Same here... Are only people that participated at the MIPT camp shown on the scoreboard?
We see a bug in Yandex.Contest standings generator that won't allow us to properly generate standing for contests with large number of registeder users (aounr 6000 for opencup rounds because of sector system). We're investigating the issue, will do our best to fix it by the next opencup round. I am very sorry for the trouble.
This bug is at least several months old =)
not exactly, contest log generation for previous opencup round took around 5 minutes and allowed teams to appear on official opencup standings (though it is definitely far from good)
The important thing on B:
You SHOULD NOT output the answer like
! 2 2
11
00
The "correct" answer is:
!
11
00
How to solve C.Array and D.Modular Knapsack?
C: Let M = min(A). If M occurs in A once, then the answer is M. Otherwise, consider the first occurence of M.
Note that, any aj such that aj > ai, j > i are useless. Thus, we can conclude that the "modulo chain" before the first occurence are strictly decreasing. Also, After passing the first occurence, the value Xi will never decrease unless it is M. We will find a set of numbers that can be the result of xi after passing the first occurence.
Then, we should find all number N such that N can be represented as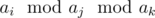 ... when ai > aj > ak. This can be done with DP. Sort A and remove duplicates. Let DP[i][j] = (true iff j is possible outcome after passing some subset of modulo chain for length-i prefix). This can be calculated easily in O(n2), and with some bitset labor you can reduce it to O(n2 / 64).
... when ai > aj > ak. This can be done with DP. Sort A and remove duplicates. Let DP[i][j] = (true iff j is possible outcome after passing some subset of modulo chain for length-i prefix). This can be calculated easily in O(n2), and with some bitset labor you can reduce it to O(n2 / 64).
D: Let's solve minimization problem instead. It seems that the one with large weights are mostly useless, as it seems they can be replaced with smaller ones. The tests are intentionally broken, so this is enough. Add the item in the order of weights, run the program for 1.45 second and quit. You can easily transform the min. problem solution into max. problem.
In C, is it like: say upto i, the bitset is B, then at i+1, you will divide the bits in a[i+1] lengths, and OR them with B to get newB? That yields, n^2log(n)/64, right? Any better way?
Exactly that. And it is N^2/64 + NlogN.
How do you get [bit_i, bit_j] quickly?
I implemented my own bitset.
Finally I solved this problem and it was really difficult for me to implement operation get_segment in bitset and what I done is something like sqrt decomposition: shift left pointer until it is on a start of some bucket (in our case bucket is an int and it's size is 32), then shift right pointer until it is on the end of some bucket and then process all buckets between left and right pointers. Processing is just splitting current bucket into two parts — one with size (32 — how_much_we_shifted_left_pointer) (head) and the other one is what is left (tail), and then save these parts in a new bitset in bucket i and i+1 respectively — head part goes to i and tail part goes to i+1 bucket.
My implementation is here. It uses long insted of int, but it doesn't matter.
It may seem overcomplicated, but this is the only proper method I can imagine. Could you share your bitset implementation or/and tell something how it works?
https://ideone.com/XGSZaC
It's so beautiful! Thank you!
Also there is deterministic solution for D with idea of convex hull and stack.
Oh, your reply reminded me a very similar problem. Unfortunately (or fortunately) I didn't remembered this in contest :p
How to solve B?
+1
How many people who wrote AC solution for B are interested in how to solve it?
Let me try. (I'm not very confident, I don't understand suffix automatons very well.)
Let's call a string of length n "row string" if it appears at least once as a row of the secret board. We want to determine all row strings. Then it's easy to recover the entire board in O(n2) more steps.
Suppose that we currently know that s1, ..., sk are row strings for sure. We want to find another row string, or conclude that there are no more row strings.
Let's construct a suffix automaton for the string s1 + 'x' + s2 + 'x' + ... + sk. For each state in this automaton, let t be the shortest string that reaches this state. Let's query "t + 'a'" in case the automaton doesn't accept it; if the secret board contains it, we can get a new row string by extending it. Do the same for t + 'b'. If we can't find new row strings this way, we've found everything.
Since we can construct the automaton incrementally, the total number of new states we get is O(n2), and the number of queries is O(n2).
The solution is to find all different rows of the table one by one and then in n2 queries restore it.
If you have found k rows, you need to find any string that is not a substring of any of these k rows. Then it can be expanded to the whole row in at most 2n queries.
Consider a trie of all substrings of already found rows. You can try to go by non-existent transitions of the trie and ask if there is such a string in the whole table, do this in the order of length increase. However, in its simplest form, it will work in cubic number of queries. Here comes the trick to make it 2n2 overall — if you already know that some substring of the string you are about to ask doesn't exist, skip this query.
If you consider the trie as a suffix automaton of k strings, you can prove this upper bound. There will be at most 2n2 states in the automaton and among all transitions by the same character from each vertex you will ask only about the shortest string, skipping the others.
When the upsolving of this and past div.2 contests will be available?
How to solve the "hellish" problem G? Is there an article on arXiv or somewhere else about this problem?
I have some kind of "editorial" for G.
Recall the algorithm for building automaton. Let's calculate expected number of cloned states then add n + 1. Consider adding last character of string s. Let t be the longest suffix which occurs more than once and let a be the character preceding t. Then vertex cloning had happened iff there is character b ≠ a such that it preceds each occurence of t except for the last one.
For string s denote sequence |s|, |π(s)|, |π(π(s))|, ... 0 as chain(s) (here π(t) is longest suffix shorter than t equals to prefix of t). Let's calculate all possible triples (chain(t), chain(at), chain(bt)), where a and b are different characters. Also for each triple we need to know the number of triples of strings (t, at, bt) which corresponds to this triple. Knowing only (chain(t), chain(at), chain(bt)), it's possible to calculate number of strings s such that vertex cloning happened.
You don't need triples. You need to calculate for each t number of strings that contain it and subtract those in which all occurences of t are preceded by the same character a. Only pairs (chain(t), chain(at)) are needed for that.
Is it really possible to solve problem J in 19 minutes or is that AC in 19 mins some kind of a hoax xd?
It took me 30 minutes to solve it, 19 mins doesn't sound crazy.
Btw how to solve it?
Suppose that all coefficients of polynomials are in F2. The key observation: P(x)2 = P(x2).
For an integer n and a polynomial Q, let f(n, Q) be the number of nonzero terms in Pn * Q.
In case n is odd, use f(n, Q) = f(n - 1, PQ).
In case n is even, first decompose Q into "even part" and "odd part": Q(x) = R(x2) + xS(x2). Then f(n, Q) = f(n / 2, R) + f(n / 2, S).
This way we reach only O(2dlogn) states.
Did you actually implement this as recursion with memoization? Because it looks like it's rather hard to fit into the memory.
rng_58's solution is cool and I think that I do mostly the same thing, but I came up with that in a very different way.
I will also use that P(x)2 = P(x2), so P(x)n = P(x2a0)P(x2a1)... P(x2am - 1). Now let's calculate (imaginary) DP[i][j]: we multiplied first i polynomials and interested in coefficient for xj (basically DP[i] is a product of i first polynomials). We can see that if j1 and j2 have different remainders modulo 2ai then they are independent, so our DP is a set of 2ai independent DPs, corresponding to different remainders modulo 2ai. Each of these DPs have only d interesting states, all other values are zeroes. So we can count the number of DPs with given mask of values in another dp, now real (in the code). We have to make transitions for imaginary DP, they will correspond to transitions in our real DP.
You're crazy, it took me rather something like 2-3 hours xd. But it seems my solution looks significantly more complicated. I didn't even use explicitly the fact that P(x)2 = P(x2), I base my solution on fact that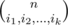 is odd iff i1, i2, ..., ik are submasks of n in binary system.
is odd iff i1, i2, ..., ik are submasks of n in binary system.
J is a well-known problem in China:
Version 1
Version 2
We were afraid that it could be well-known(
OK, "HDU-coach" team name and this question being asked on HDU online judge explains a lot, I suspected that's likely reasonable explanation.
How to solve A, E, H?
H: Note that if k is the largest value of a n-beautiful multiset A, then the elements of A that are smaller than k have to form a k - 1-beautiful multiset. If there are x copies in k, then we get x·k + (k - 1) = n, so k is a proper divisor of n + 1. Conversely, taking such a k and adding x copies of k to a k - 1-beautiful multiset, we always get a n-beautiful multiset. We can hence use dp to compute the number and total size of n-beautiful mutisets as follows
The number of states used in computing DP[n] is equal to the number of divisors of n + 1.
Edit: Does someone have a good bound on the number of divisors summed over divisors of n to bound the total runtime? (Something better than this comment.)
Actually, intended solution for H was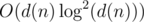 with convolution repeated
with convolution repeated 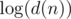 times, but we failed to set time limit properly.
times, but we failed to set time limit properly.
If number of good pairs of good divisors for maxtests is something like d(n)2 / 60 (with d(n) ≈ 60000 then good luck with distinguishing it from :P
:P
Yes, the number of good pairs is around 107, but I also had to index all the states properly. I wrote solutions with a binary search and a trie to do indexing on dp states, and they both worked very slow comparing to the main solution. My bad I didn't force somebody not so retarded in writing fast solutions to try to fit this into TL.
But anyway, the possible solution would only be to increase constraints to 1018 (and make bigger TL also). I'd say it's controversial whether it'd really improve the problem.
I agree that indexing is some kind of an issue we should deal with (and I used unordered_map for this on beginning), but it can be easily solved by computing corresponding indices recursively along with other info we compute (I was not sure whether by last sentence in first paragraph you meant that you're retarded cause you didn't notice it or whether because you didn't try hard enough to do some other optimizations)
A: Let's say that ai dominates aj if i, j are incompatible and ai > aj. For every k, we can color it with the length of the longest dominating chain ending with ak (so ak the the largest element in the chain). Note that is is optimal, as every chain forms a clique.
To compute the coloring quickly, we compute for every bitmask m two numbers: The largest color C of a value ai contained in the mask and the maximum number D of bits in which some such ai differs from m. If m occurs in a and D ≥ k, then we increment C and set D to 0. From every mask, we can transition to other masks by setting another bit. The total runtime is O(22·222 + n).
I also had a funny issue where declaring
array<pair<int8_t, uint8_t>, 1<<22>exceeded the compiler memory limit for some reason.E: For every node we'll compute the total cost if the capital was placed there. This can be done efficiently with centroid decomposition.
For a fixed centroid C, we root at C and compute for every vertex v the contribution of towers t not located in the subtree of C containing v. For a fixed tower t, its contribution on a vertex v in a different subtree only depends on the depth (=distance from v to C). Moreover, as a function of this depth, the contribution is piece-wise constant with pieces of length k (and an infinitely long piece for 0), so we can efficiently get the total contribution for every depth by prefix-summing over each residue class mod k separately, then prefix summing over the whole array.
To deal with the whole not-in-its-subtree, we compute the contribution of every subtree (only for depth up to the height of the subtree) and the total contribution for every depth. The total runtime is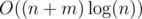 , even for k up to n.
, even for k up to n.
Can I be solved in O(nlogn)?
Can you tell the easier (slower?) approach, please? :D
After the contest BledDest told me the solution and also mentioned that it's about the same as in 911G - Mass Change Queries. I can't believe that's what everybody submitted, looks really advanced to me tbh. :D
solution and also mentioned that it's about the same as in 911G - Mass Change Queries. I can't believe that's what everybody submitted, looks really advanced to me tbh. :D
Let's maintain the segment tree over the queries (segments). At the beginning every node is the identity 2x2 matrix. The merge is matrix multiplication. Then you process all 2n ends of segments in the ascending order. When reaching the beginning of some segment, update the corresponding node in the segment tree with matrix ((100 — p, p), (p, 100 — p)), the end is back to identity matrix. The answer for the end is the root of the tree.
You can just build a lazy segtree (where you only do updates, no queries) over the positions, where the lazy stores the probability of being repainted. The lazy-merge function is similar to what you get with your matrix multiplication: merge(p1, p2) = (1 - p1)p2 + p1(1 - p2). First compress the li and ri to 0, ..., 2n - 1. For every request, you update [li, ri - 1] with p. Then you push all updates down to the leaves of the segment tree. For every leaf, you add it's value times the length of the corresponding uncompressed segment to the answer. Total runtime is .
.
Ye, it's not the application of ST that seems advanced to me but that presence of ST by itself. Like that path I took was about "do the basic events sort thingy; however, we want to delete elements, that would require matrix division". Then I coded some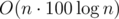 (so it would not require division, like recalcing the whole dp with matrix exponentiation on each step) that somehow turned not precise enough, I believe (or that WA was purely of my bad implementation). I can't understand what should have pushed me to think about ST.
(so it would not require division, like recalcing the whole dp with matrix exponentiation on each step) that somehow turned not precise enough, I believe (or that WA was purely of my bad implementation). I can't understand what should have pushed me to think about ST.
My solution is in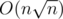 . It's unnecessarily complicated. Basically, I have decomposed the segments into
. It's unnecessarily complicated. Basically, I have decomposed the segments into  chunks. Then proceeding the events from left to right, when an enter/exit event occurs we have to update it's corresponding chunk in time order of chunk size. By updating, for each chunk we will keep the probability of taking odd segments from this chunk. Each query can be answered in
chunks. Then proceeding the events from left to right, when an enter/exit event occurs we have to update it's corresponding chunk in time order of chunk size. By updating, for each chunk we will keep the probability of taking odd segments from this chunk. Each query can be answered in  by going over the values calculated for each chunk.
by going over the values calculated for each chunk.
It was not the intended solution. I had to optimize a lot to ACe it. However, what I was doing in my solution can be done with a segment tree too. But I didn't notice during contest time.
My solution is the same and the only thing I had to optimize is to replace
List<Integer>toint[]. I thought it would be absolutely useless, but it worked =)This solution doesn't seem complicated as for me. And yes, after the contest I realized that it worked for 0.983s.
I had some wrong ideas at the beginning and wrote more complicated O(pn) solution (p = 101). I basically maintain the count for each pi, and compute the matrix multiple in O(p) time with appropriate precomputation.
What are those precomputations? It seems, I can't squeeze my by any means)
by any means)
WLOG assume 0 ≤ Li < Ri ≤ 2N. For each interval [i, i + 1] we can have the histogram of each pi occurence with difference arrays. Let qpi be such occurence. Then we want to calculate M0q0 × M1q1 × ... when Mi is the state transition matrix for probability i. We can simply precompute those powers in O(pn) time, Now we can calculate the answer in O(p) time.
Oh, I thought about the difficulty of storing all of them and never even cosidered multiplying them right away. Nice approach, thanks)
This is probably the fastest to code solution.
I tried to implement the same idea after the contest, but got WA. Probably because I did multiplication/division instead of log addition/subtraction which cost a lot of precision error. How did you know that you need to do the calculations in logarithmic scale at first?
It's a common practice actually, without logarithms it's possible to construct a test in which at first the product becomes very small (of order 2 - n), and after that it becomes close to 1 again, but the precision is lost in the first phase.