Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
cin >> t;
for (int i = 0; i < t; ++i) {
int x;
cin >> x;
cout << x / 2 << endl;
}
return 0;
}
Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
cin >> t;
for (int i = 0; i < t; ++i) {
string s;
cin >> s;
sort(s.begin(), s.end());
if (s[0] == s.back()) cout << -1 << endl;
else cout << s << endl;
}
return 0;
}
1093C - Mishka and the Last Exam
Tutorial
Tutorial is loading...
Solution (PikMike)
n = int(input())
l, r = 0, 10**18
b = list(map(int, input().split()))
a = [0 for i in range(n)]
for i in range(n // 2):
a[i] = max(l, b[i] - r)
a[-i - 1] = b[i] - a[i]
l, r = a[i], a[-i - 1]
print(*a)
Naive (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const long long INF64 = 1'000'000'000'000'000'000ll;
const int N = 200 * 1000 + 13;
int n;
long long a[N], b[N];
void brute(int x, long long l, long long r){
if (x == n / 2){
forn(i, n)
printf("%lld ", a[i]);
puts("");
exit(0);
}
for (long long i = l; i <= b[x] / 2; ++i) if (b[x] - i <= r){
a[x] = i;
a[n - x - 1] = b[x] - i;
brute(x + 1, i, b[x] - i);
}
}
int main() {
scanf("%d", &n);
forn(i, n / 2)
scanf("%lld", &b[i]);
brute(0, 0, INF64);
return 0;
}
Tutorial
Tutorial is loading...
Solution (Ajosteen)
#include <bits/stdc++.h>
using namespace std;
const int N = int(3e5) + 999;
const int MOD = 998244353;
int n, m;
vector <int> g[N];
int p2[N];
int cnt[2];
int col[N];
bool bad;
void dfs(int v, int c){
col[v] = c;
++cnt[c];
for(auto to : g[v]){
if(col[to] == -1) dfs(to, 1 - c);
if((col[v] ^ col[to]) == 0)
bad = true;
}
}
int main() {
p2[0] = 1;
for(int i = 1; i < N; ++i)
p2[i] = (2 * p2[i - 1]) % MOD;
int tc;
scanf("%d", &tc);
while(tc--){
scanf("%d%d", &n, &m);
for(int i = 0; i < n; ++i)
g[i].clear();
for(int i = 0; i < m; ++i){
int u, v;
scanf("%d %d", &u, &v);
--u, --v;
g[u].push_back(v);
g[v].push_back(u);
}
int res = 1;
for(int i = 0; i < n; ++i) col[i] = -1;
for(int i = 0; i < n; ++i){
if(col[i] != -1) continue;
bad = false;
cnt[0] = cnt[1] = 0;
dfs(i, 0);
if(bad){
puts("0");
break;
}
int cur = (p2[cnt[0]] + p2[cnt[1]]) % MOD;
res = (res * 1LL * cur) % MOD;
}
if(!bad) printf("%d\n", res);
}
return 0;
}
1093E - Intersection of Permutations
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int N = 200 * 1000 + 13;
int n, m;
int a[N], b[N], pos[N];
vector<int> f[N];
vector<int> vals[N];
void addupd(int x, int y){
for (int i = x; i < N; i |= i + 1)
vals[i].push_back(y);
}
void addget(int x, int y){
if (x < 0 || y < 0) return;
for (int i = x; i >= 0; i = (i & (i + 1)) - 1)
vals[i].push_back(y);
}
void upd(int x, int y, int val){
for (int i = x; i < N; i |= i + 1)
for (int j = lower_bound(vals[i].begin(), vals[i].end(), y) - vals[i].begin(); j < int(f[i].size()); j |= j + 1)
f[i][j] += val;
}
int get(int x, int y){
if (x < 0 || y < 0) return 0;
int res = 0;
for (int i = x; i >= 0; i = (i & (i + 1)) - 1)
for (int j = lower_bound(vals[i].begin(), vals[i].end(), y) - vals[i].begin(); j >= 0; j = (j & (j + 1)) - 1)
res += f[i][j];
return res;
}
struct query{
int t, la, ra, lb, rb;
query(){};
};
query q[N];
int main() {
scanf("%d%d", &n, &m);
forn(i, n){
scanf("%d", &a[i]);
--a[i];
pos[a[i]] = i;
}
forn(i, n){
scanf("%d", &b[i]);
--b[i];
b[i] = pos[b[i]];
}
forn(i, m){
scanf("%d", &q[i].t);
if (q[i].t == 1){
scanf("%d%d%d%d", &q[i].la, &q[i].ra, &q[i].lb, &q[i].rb);
--q[i].la, --q[i].ra, --q[i].lb, --q[i].rb;
}
else{
scanf("%d%d", &q[i].lb, &q[i].rb);
--q[i].lb, --q[i].rb;
}
}
vector<int> tmp(b, b + n);
forn(i, n) addupd(i, b[i]);
forn(i, m){
if (q[i].t == 1){
addget(q[i].rb, q[i].ra);
addget(q[i].lb - 1, q[i].ra);
addget(q[i].rb, q[i].la - 1);
addget(q[i].lb - 1, q[i].la - 1);
}
else{
addupd(q[i].lb, b[q[i].lb]);
addupd(q[i].rb, b[q[i].rb]);
swap(b[q[i].lb], b[q[i].rb]);
addupd(q[i].lb, b[q[i].lb]);
addupd(q[i].rb, b[q[i].rb]);
}
}
forn(i, n) b[i] = tmp[i];
forn(i, N){
sort(vals[i].begin(), vals[i].end());
vals[i].resize(unique(vals[i].begin(), vals[i].end()) - vals[i].begin());
f[i].resize(vals[i].size(), 0);
}
forn(i, n)
upd(i, b[i], 1);
forn(i, m){
if (q[i].t == 1){
int res = 0;
res += get(q[i].rb, q[i].ra);
res -= get(q[i].lb - 1, q[i].ra);
res -= get(q[i].rb, q[i].la - 1);
res += get(q[i].lb - 1, q[i].la - 1);
printf("%d\n", res);
}
else{
upd(q[i].lb, b[q[i].lb], -1);
upd(q[i].rb, b[q[i].rb], -1);
swap(b[q[i].lb], b[q[i].rb]);
upd(q[i].lb, b[q[i].lb], 1);
upd(q[i].rb, b[q[i].rb], 1);
}
}
return 0;
}
Tutorial
Tutorial is loading...
Solution (Ajosteen)
#include <bits/stdc++.h>
#define fore(i, l, r) for(int i = int(l); i < int(r); ++i)
#define forn(i, n) fore(i, 0, n)
#define nfor(i, n) for(int i = int(n) - 1; i >= 0; --i)
#define for1(i, n) for(int i = 1; i < int(n); ++i)
#define mp make_pair
#define pb push_back
#define sz(a) int((a).size())
#define all(a) (a).begin(), (a).end()
#define x first
#define y second
#define correct(x, y, xmax, ymax) ((x) >= 0 && (x) < (xmax) && (y) >= 0 && (y) < (ymax))
#define max(a, b) ((a > b)? a : b)
#define min(a, b) ((a < b)? a : b)
#define abs(a) ((a < 0) ? -a : a)
#define sqr(a) (a * a)
using namespace std;
const int N = int(1e5);
const int M = 105;
const int MOD = 998244353;
int sum(int a, int b){
return (a + b) % MOD;
}
int n, k, len;
int a[N];
int dp[N][M];
int sumdp[N];
int cnt[M][N];
int main() {
scanf("%d %d %d", &n, &k, &len);
forn(i, n){
scanf("%d", a + i);
if(a[i] != -1) --a[i];
}
forn(i, k)
forn(j, n)
cnt[i][j + 1] = cnt[i][j] + (a[j] == i || a[j] == -1);
forn(i, n){
forn(j, k){
if(!(a[i] == -1 || a[i] == j))
continue;
int add = 1;
if(i > 0) add = sumdp[i - 1];
dp[i][j] = add;
bool ok = i + 1 >= len;
int l = max(0, i - len + 1);
int r = i + 1;
ok &= (r - l == cnt[j][r] - cnt[j][l]);
if(!ok) continue;
if(i + 1 == len){
dp[i][j] = sum(dp[i][j], MOD - 1);
continue;
}
add = sum(dp[i - len][j], MOD - sumdp[i - len]);
dp[i][j] = sum(dp[i][j], add);
}
forn(j, k) sumdp[i] = sum(sumdp[i], dp[i][j]);
}
printf("%d\n", sumdp[n - 1]);
return 0;
}
1093G - Multidimensional Queries
Tutorial
Tutorial is loading...
Solution (BledDest)
#include <bits/stdc++.h>
using namespace std;
const int N = 200043;
const int INF = int(1e9);
int T[4 * N][32];
int A[4 * N][5];
int n, k;
void build(int v, int l, int r)
{
if(l == r - 1)
{
for(int i = 0; i < (1 << k); i++)
{
int cur = 0;
for(int j = 0; j < k; j++)
if(i & (1 << j))
cur += A[l][j];
else
cur -= A[l][j];
T[v][i] = cur;
}
}
else
{
int m = (l + r) / 2;
build(v * 2 + 1, l, m);
build(v * 2 + 2, m, r);
for(int i = 0; i < (1 << k); i++)
T[v][i] = min(T[v * 2 + 1][i], T[v * 2 + 2][i]);
}
}
int query(int v, int l, int r, int L, int R, int x)
{
if(L >= R) return INF;
if(L == l && R == r)
return T[v][x];
int m = (l + r) / 2;
return min(query(v * 2 + 1, l, m, L, min(R, m), x), query(v * 2 + 2, m, r, max(L, m), R, x));
}
void upd(int v, int l, int r, int z)
{
if(l == r - 1)
{
for(int i = 0; i < (1 << k); i++)
{
int cur = 0;
for(int j = 0; j < k; j++)
if(i & (1 << j))
cur += A[l][j];
else
cur -= A[l][j];
T[v][i] = cur;
}
}
else
{
int m = (l + r) / 2;
if(z < m)
upd(v * 2 + 1, l, m, z);
else
upd(v * 2 + 2, m, r, z);
for(int i = 0; i < (1 << k); i++)
T[v][i] = min(T[v * 2 + 1][i], T[v * 2 + 2][i]);
}
}
int main()
{
scanf("%d %d", &n, &k);
for(int i = 0; i < n; i++)
{
for(int j = 0; j < k; j++)
{
scanf("%d", &A[i][j]);
}
}
int q;
scanf("%d", &q);
build(0, 0, n);
for(int i = 0; i < q; i++)
{
int t;
scanf("%d", &t);
if(t == 1)
{
int z;
scanf("%d", &z);
--z;
for(int j = 0; j < k; j++)
scanf("%d", &A[z][j]);
upd(0, 0, n, z);
}
else
{
int ans = 0;
int l, r;
scanf("%d %d", &l, &r);
--l;
for(int i = 0; i < (1 << (k - 1)); i++)
{
int x = query(0, 0, n, l, r, i);
int y = query(0, 0, n, l, r, ((1 << k) - 1) ^ i);
ans = max(ans, abs(x + y));
}
printf("%d\n", ans);
}
}
return 0;
}
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int N = 200 * 1000 + 13;
const int INF = 1e9;
struct point{
int a[5];
point(){};
int& operator[](int x){
return a[x];
}
};
int n, k;
point a[N];
int t[32][4 * N];
int apply(point& p, int mask){
int res = 0;
forn(i, k){
res += (mask & 1 ? p[i] : -p[i]);
mask >>= 1;
}
return res;
}
void build(int v, int l, int r){
if (l == r - 1){
forn(mask, 1 << k)
t[mask][v] = apply(a[l], mask);
return;
}
int m = (l + r) / 2;
build(v * 2, l, m);
build(v * 2 + 1, m, r);
forn(mask, 1 << k)
t[mask][v] = min(t[mask][v * 2], t[mask][v * 2 + 1]);
}
void upd(int v, int l, int r, int pos, point& val){
if (l == r - 1){
forn(mask, 1 << k)
t[mask][v] = apply(val, mask);
return;
}
int m = (l + r) / 2;
if (pos < m)
upd(v * 2, l, m, pos, val);
else
upd(v * 2 + 1, m, r, pos, val);
forn(mask, 1 << k)
t[mask][v] = min(t[mask][v * 2], t[mask][v * 2 + 1]);
}
int bst[32];
void get(int v, int l, int r, int L, int R){
if (L >= R)
return;
if (l == L && r == R){
forn(mask, 1 << k)
bst[mask] = min(bst[mask], t[mask][v]);
return;
}
int m = (l + r) / 2;
get(v * 2, l, m, L, min(m, R));
get(v * 2 + 1, m, r, max(m, L), R);
}
int main() {
scanf("%d%d", &n, &k);
forn(i, n) forn(j, k)
scanf("%d", &a[i][j]);
build(1, 0, n);
int m;
scanf("%d", &m);
forn(_, m){
int t;
scanf("%d", &t);
if (t == 1){
int i;
scanf("%d", &i);
--i;
point tmp;
forn(j, k)
scanf("%d", &tmp[j]);
upd(1, 0, n, i, tmp);
}
else{
int l, r;
scanf("%d%d", &l, &r);
--l, --r;
forn(mask, 1 << k)
bst[mask] = INF;
get(1, 0, n, l, r + 1);
int ans = 0;
forn(mask, 1 << k)
ans = max(ans, abs(bst[(1 << k) - 1 - mask] + bst[mask]));
printf("%d\n", ans);
}
}
return 0;
}










Can someone link this editorial to the contest materials?
Done
Can someone explain the Intersection of Permutations editorial in more detail?
You can read about 2D-BIT at topcoder.
The idea about offline trick comes from the treap implementation. With treap you would do something like: for each BIT x in query sum up the amount of numbers which are less than or equal to y. Imagine processing the same thing with BIT. At first glance it seems like you would need to do operations "add 1 in y" and "get prefix sum up to y". However, you don't need all the points up to max coordinate. You can compress the numbers in each BIT and find needed position with binary search.
deleted
Can anybody help me why I m getting Runtime Error On Test Case 9 in The Most Discussed Beautiful Graph Problem My solution.
You have set N = 10^5, but it can be 3 x 10^5. :)
Could someone tell me why I got TLE in problem D? Here's my submission. Thanks a lot!
Number of test cases = 3e5, and for each test case you memset the whole colour array and first array, which are also 3e5.
It is stated that it is guaranteed that summation N over all test cases doesnt exceed 3e5, so for each test you should manually loop on array 0->n and clear it yourself, which gives a total accepted complexity of 3e5 over all test cases.
Here is your 47162894 updated :D
Thank you for your detailed explanation, which helped me a lot :D
Its okay :D, I also got time limit for this reason in the contest :(
It's giving me runtime error on Scanner Class.
https://codeforces.com/contest/1093/submission/47155880
Every time I got stuck with this scanner shit.Please give me any alternative.
Please help me
The only reason i can think of is u have used 2 Scanner objects to scan from same source.
I think this is ur solution
Is there a recursive(with memoization) implementation of Problem F? I didn't fully get the editorial.
You can code it recursively but it won't look easier. I can tell you my more straightforward approach.
Let it be the same dp and sdp definitions. Now you want to update dp[i][lst] by making the last segment of value lst. That means that there is some position prv, where the segment of maximum length of value lst could start (this length is found with len and position of the rightmost element not equal to - 1 or lst.
Thus you want to sum up all the dp[j][l] for j = prv... i - 1 and l = 1... k, that is sdp[j]. However, the previous segment couldn't end with lst, subtract dp[j][lst].
Add a little bit of maintaining partial sums over both dp and sdp arrays and you'll get the same complexity.
Code
Can anyone explain to me why problem F's solution is right?
Can someone explain the reason behind solving 2^a+2^b in problem D ?
The last sentence explains it? If the graph is bipartite then the only coloring exists (color vertices of the first partition white and the second is black). White is one of {1, 3}, black is {2}. That is 2size colorings. And then change white to {2} and black to {1, 3}.
Hard to Understand the solution of D. What have changed if there were only two numbers 1 and 2(not 3).Please explain the reason for 2^a + 2^b .
1 and 3 are the same in terms of making pairs. So you can put either 1 or 3 on each vertex, that is 2 options. Thus it's 2size. With only 1 and 2 you'll have a single option for each vertex, it would be just 1.
Then why, 2^size for both parts. By your explanation it should be 2^a for one part(1,3) and simply 1 for another part(2).
Can also you explain why res = res * cur for each iteration on Node in Code.
It is 2a for part {1, 3} and 1 for part {2}. But then you swap parts and color the first part {2} and the second part {1, 3}.
The colorings on each connected component are independent, so we multiply their answers.
Can someone help me out with my code? I did exactly what is mentioned in the tutorial however couldn't pass the second pretest during the contest. Here is the link to my code: https://ideone.com/jWlp4l
Shouldn't fl be the other way around? The answer is 0 if at least one connected component isn't bipartite.
Oh! Didn't take care of that. Thanks, it worked by changing fl the other way round. Was a little bit confused.
Can someone help me out with my code? It kept getting Runtime Error on Test Case 10 in problem E. I'm using persistent segment tree and I can't find anything wrong with it. Here is my code. Thank you so much if you could help me figure out the problem.
Another approach for problem F:
Let dp[i][j][k] : the number of ways of fill the firsts i elements where j is the last element and appear k times, this is O(N * K * N) in memory, but only need dpi - 1 for update dpi so the memory become O(N * K).
Looking what happen into the transition when a element x come? There is two cases:
x ≠ - 1: how the element is fixed dp[j][k] will be 0 except for j = x, more precisely dp[j] should be shift one position because all the ways of end with j increase by 1, and a new value should by put in dp[x][1], these value is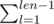 such that l ≠ j
such that l ≠ j 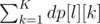 , in other words all the ways of end with other element, and if dp[x][len] become greater that 0 then make it 0, because this is a invalid array.
, in other words all the ways of end with other element, and if dp[x][len] become greater that 0 then make it 0, because this is a invalid array.
x = - 1: fix every possible element and do the same as for x ≠ - 1 K times.
So i need something that support insert one element in the front and delete in the back, and have the sum of all of it's values, this is possible with a deque!!!
Keeping K deque one for each possible element the transition can be done in O(K), and the time complexity become O(N * K).
For more details of the implementation see my code:
47081307
Can someone explain me, In the F problem.. Why are we subtracting dp(cnt-len,lst) as well and not only sdp(cnt-len). Thank you.
If you don't connect new correct segment of color lst with some previous one then you'll never break any conditions. And if optimal answer has these segments merged then you'll still visit this state.
Where does this color come from? Are you saying that gray is much far from Red? :P
For Problem F... I still can not understand why the number of the bad status is sdpcnt - len-dpcnt - len, lst,can you explain it more specifically?Thx...
From what I understand, the soln for G will NOT work if the queries is asking for minimum distance, right? Is there some other way to solve it if the problem asks for minimum?
if((col[v] ^ col[to]) == 0) bad = true; anyone please explain the working of the statement from the editorial of BEAUTIFUL GRAPH??
If two neighbor vertices have numbers 2 or {1,3} both then sum would become even. So it's checking this only. Like col[1]=1 and col[2]=1 then col[1]^col[2]=0.
For problem E, I don't understand what the tutorial is talking about. What is "update in point and sum on rectangle"? And how exactly are we remunerating the numbers?
Edit: Finally got it, I was imagining you meant reordering rather than renumbering. So for example if
a = [5, 1, 4, 2, 3, 6] b = [2, 5, 3, 1, 4, 6] then the new b should be [4, 1, 5, 2, 3, 6], changing each number in b to the position of the corresponding element in a. So the first element in b becomes 4 because the index of 2 in a is 4.
Despite what they said in the editorial sqrt decomposition is fast enough to pass E. General idea split a and b into chunks. Each chunk of b has a segment tree that keeps track of how terms the chunk has in common with all other chucks of a. Updates take
chunks. Each chunk of b has a segment tree that keeps track of how terms the chunk has in common with all other chucks of a. Updates take  , since you have to update at most four segment trees. For the other type of query you brute force part of the query so you only have to deal with intersections between whole chunks of a and whole chunks of b. Then for each chunk of b contained in the query you use the segment tree to find the number of terms it has in common with all chunks of a contained in the query. Worst case complexity for queries is
, since you have to update at most four segment trees. For the other type of query you brute force part of the query so you only have to deal with intersections between whole chunks of a and whole chunks of b. Then for each chunk of b contained in the query you use the segment tree to find the number of terms it has in common with all chunks of a contained in the query. Worst case complexity for queries is 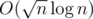 . Final complexity
. Final complexity 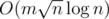 , and yes this is fast enough to pass. My code 47287195.
, and yes this is fast enough to pass. My code 47287195.
I used a similar sqrt-decomposition technique with BIT. One important thing to note is block size you choose can have a big impact on your runtime. For my implementation, I was updating the BITs for each block frequently, so it was advantageous for me to choose a larger block size. With a block size of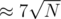 , I was able to get it to run under 2000 ms, faster than the official soln. 47315299
, I was able to get it to run under 2000 ms, faster than the official soln. 47315299
That makes sense to use a larger block size. It seems like the trade off is between how far you travel to get to the ends and starts of blocks in the brute force part which favours a smaller block size and how many blocks you have to iterate over in the segment tree/BIT query part which favours a larger block size. The second part is more costly because there is an extra log factor when you do the queries. I suspect you could use calculus to figure out the optimal block size.
For my implementation a block size is much slower (3931 ms) than
is much slower (3931 ms) than  (2558 ms). The best block size that I have found for my implementation is
(2558 ms). The best block size that I have found for my implementation is  it gets (1825 ms) 47317374.
it gets (1825 ms) 47317374.
It is interesting how a similar sqrt-decomposition approach can have such different optimal block sizes.
Problem D Can someone help me? My solution is giving TLE on test case 13 https://codeforces.com/contest/1093/submission/47291028
1093A
https://codeforces.com/contest/1093/submission/47239530
Why was this solution not accepted? Can somebody help?
plz the read all the information on your soultion page. it says your ans is wrong for xi = 36
Anybody please explain why 2^a+2^b work in problem 1093D — Beautiful Graph.I need mathematical proof.Please help
You have two parts of size a and b, we want to proof that one of them should be totally odd and one of them should be even. We obtain this fact using induction on length of a path. We assume that vertices of this path should be like: odd,even,odd,even,... now erase the last vertex and we can apply to induction hypothesis, after that add this vertex and the erased edge. Since one of the endpoint of that edge is odd(for example), this vertex should be even. So for each two vertex in same part, they should be as same cause length of every path between them is even. Now there is two case: 1:part with a vertices be odd, we have 2^a to choose that every vertex should be 1 or 3. 2:part with b vertices be odd, we have 2^b like previous case.
Thanks for problem G, short and nice.
can anyone explain me the last statement in pikmike solutions forn(mask, 1 << k) ans = max(ans, abs(bst[(1 << k) — 1 — mask] + bst[mask])); printf("%d\n", ans);
In bst I have the minimum value for each mask (the values of ci of editorial). And I also know that ci will have all its signs turned if I replace 0 with 1 in mask and 1 with 0. That is the same as doing (2k - 1)^mask (or minus as I do). Thus bst[(2k - 1)^mask] will have the maximum value of mask but with multiplied by -1. I wanted to update the answer with (max - min) and I have min and ( - max). So I can do ( - ( - max) - min) or |max + min| (as I surely will have the non-negative value in a result).
all clear.
In tutorial for problem G, should time complexity be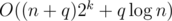 for the code you give? I think they are quite different.
for the code you give? I think they are quite different.
What makes you think that?
In your code, it cost you time on the segment tree and O(2k) time to modify or update
time on the segment tree and O(2k) time to modify or update 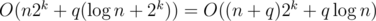 . To get the result
. To get the result 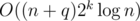 , we could build 2k segment trees, and I got TLE when implementing this(my submission). Actually, the difference occurs when dealing with query and modification, one is
, we could build 2k segment trees, and I got TLE when implementing this(my submission). Actually, the difference occurs when dealing with query and modification, one is 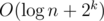 each time and the other is
each time and the other is 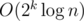 , which makes me think they are quite different.
, which makes me think they are quite different.
bstafter it for each modification or query. The time used when building the tree is O(n2k). Thus the time complexity isIt costs me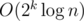 on both update and get queries. There are loops of 2k iterations on each of these functions. I also do have 2k segment trees, it's just the traversal order that differs. I have the other submission, which does about the same as yours and it works twice as slow. It seems, you should consider the time spent jumping around in memory while implementing it.
on both update and get queries. There are loops of 2k iterations on each of these functions. I also do have 2k segment trees, it's just the traversal order that differs. I have the other submission, which does about the same as yours and it works twice as slow. It seems, you should consider the time spent jumping around in memory while implementing it.
I got it. Thanks for your explanation and sorry to take up your time.
While I (somewhat) understand how the solution to problem E works, and I've also read the article on Topcoder (about BIT, and another about RMQ),
I really don't understand how to come up with such a solution , the rectangle method seems quite non-intuitive .... can someone give any suggestions on this based on their own experience ?
Thanks a lot !
To be fair, problems of kind "answer something on a segment" don't come in lots of different forms. Like all of them are divided into:
This problem clearly doesn't fit into Mo category, prefix is also kinda weird here. Thus is probably segment tree or some other online structure.
And there is another common trick. When you have several synchonized permutations but the exact values on them doesn't matter, you can renumerate one of them to identity permutation. I personally met this technique quite a few times.
Hi PikMike,
Thank you for taking out the time to answer my question.
Could you kindly clarify what you mean when you say "renumerate one of them" ? Do you mean getting rid of one of the permutations by finding a common property of the elements of the permutation (like in this question we reduce 2 permutation arrays to a single array by representing each number as a coordinate) ?
Yeah, essentially it is getting rid of one permutation. In some cases you can just abandon this one, in some you will still need it (but at least in will be 1, 2, ..., n). The latest problem on this trick I remember should be 1043D - Mysterious Crime.
Need help for problem G, from what i understand from the tutorial, we will build 2k segment tree, each tree will be based on the value of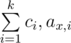 , then we will take the maximum and the minimum of each 2k and take optimal distance as the result, is this right? and how can do this since each of |ax, i - ay, i| already has their fixed ci?
, then we will take the maximum and the minimum of each 2k and take optimal distance as the result, is this right? and how can do this since each of |ax, i - ay, i| already has their fixed ci?
You don't take arbitrary ci but the opposing ones. Take the easiest case — point x is larger on each coordinate than point y. Thus, you'll need cx be all ones and cy be all minus ones. However, for any other pair of opposing in each position values of c the sum will not exceed the appropriate pair. This concludes that the right values of cx and cy will have the maximum result of all candidates. The other cases of relative positions also follow the same principle.
Hi @pikmike, i was solving october Long challenge and that has question very similar to question G . Can you please explain how we are querying the max and min in the range ??
I think the naive solution for Mishka and the Last Exam is not correct. It's getting TLE on the 9th test case. http://codeforces.com/contest/1093/submission/47462619 Or Should it get a TLE that's why it is the naive solution?
Yeah, it's TL but much simpler logic. That's why it's called naive.
can someone explain PROBLEM E in easier manner? i really confused.
Try reading the topcoder article and then read this on SO: https://stackoverflow.com/questions/15439233/bitusing-a-binary-indexed-tree
I think the SO explanation was decent. Visualize the
1) Query operation: going backwards (from a leaf node) on the right link.
2) Update operation: going backwards (from a leaf node) along left link,
The solution to problem E will simply extend this to both x and y dimensions. The GeeksforGeeks article also explains this well with a diagram: https://www.geeksforgeeks.org/two-dimensional-binary-indexed-tree-or-fenwick-tree/
Thanks for the article, but what is
addupdandaddgetfor? Especially thei |= i+1part and why do we have to sort them?In problem E, square root decompsition + binary indexed tree solution is getting accepted, when block_size is fixed about 800, but getting TLE when block_size is used by sqrt(n). In both solution each update is O(4*logn) and each query is O(2*block_size + (n/block_size)*logn) and pre build is O(nlogn).
So, is data set weak for problem E? Isn't it possible to create such input so that this solution can't get accepted?
Accepted using block_size = 800: 47504503
TLE on test 16 using block_size = sqrt(n): 47504554
**Update: ** Accepted solution runs in about 2.5 sec, when block_size is 1700.
My algorithm with block_size sqrt(n)[about 500] get Accepted. 96324829. I think it's not necessary use BIT and vector is enough.
I keep getting TLE in D on test case 22. Can anyone tell me what's the problem? Here's my solution.
u should set by hand, not memset ! With memset u get a complexity of O(N) so a total of O(N ^ 2). setting it by hand would result in a complexity of O(N) because the sum of N over all test cases is smaller than 3e5
Can somebody help me with my code on F ? I checked myself many times with the provided code but i find nothing suspicious. I get WA on test 4 47825046
Please, someone, suggest me some material of how to compress numbers in a 2D BIT. I am unable to get how Editorialist of the Problem E is compressing the numbers in each BIT.
I am getting wrong answer in prob. D, test case 3,that is , for some cases my code is giving output 0, anybody got any ideas? Link to the code :
Nevermind , I solved it :D
Hello, can anyone explain to me why my code of problem "D-Beautiful Graph" is not working? I tried to make it as similar to example code as possible but still does not work. my code
I did the same approach as Editorial for problem D but I got wrong answer at test 3. Could anyone help me figure out what wrong with my submission 62551741
I found out the bug.