Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 9 | TheScrasse | 144 |
| Name |
|---|



thanks for the tutorial!
How to split sequence into |LIS| decreasing sequence in E?
We'll use the "standard" LIS algorithm with binary searching: sweep through the array, and maintain an array of
dp[l] = min(A[i] s.t. there's an increasing sequence of length l ending at A[i]).When we see a new value
A[k], we binary search and find the maximum lengthlsuch thatdp[l] < A[k]; then we know there's an increasing sequence of lengthl+1ending atA[k]. Also,lis maximal, sodp[l+1] > A[k], so we should updatedp[l+1] = A[k].Now, note that the sequence over time of values of
dp[l]is decreasing. Thus, these are precisely a partition of the permutation into |LIS| decreasing subsequences, so we can store a vector for eachdp[l], and get the subsequences.But why is its running time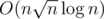
The running time of the LIS algorithm is only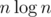 , but we have to run it
, but we have to run it  times because we're slowly removing one LIS at a time.
times because we're slowly removing one LIS at a time.
thanks
where does the Youtube tutorial go? :/
For 1097D why is the result multiplicative?
If you calculate the expected value for a given n with k = 1 (one step), you see that the answer is simply σ1(n) / σ0(n), where σ1(n) denotes the sum of divisors of n and σ0(n) the number of divisors.
It's well known that σ1 and σ0 are multiplicative functions (and easy to prove indeed). So, it's easy to see from there using induction that the function is multiplicative.
I wasn't sure when I was in the contest, so I used DFS to search all the divisors of n, the complexity is correct.
E[f(X)g(Y)] = E[f(X)]×E[g(Y)], if X and Y are independent. Here exponents of each prime divisor of N are independent of each other, and E(.) denotes the expectation value.
can anyone help me with problem B
Since the constrains are small, u can apply brute force, a simple approach is that for every given angle u can consider rotating it either clockwise(+) or anti-clockwise(-). Do it for all the angles in the array and keep summing them, if in one of the ways u get a final sum(after one complete traversal of array) which is divisible by 360, then output 'yes' other wise if non of the ways satisfy the condition sum%360==0 then output 'no'. There are total 2^15 ways(maximum) of obtaining the final sum. Refer to my solution for more clarity. https://codeforces.com/contest/1097/submission/47914337
Yes, we can approach all the possible combinations using bit masking
How to calculate dp(k,j) in problem D.
sum ( dp(k -1,j + i) * (1 / (j + i + 1)) ), i goes from 0 to (p -j). Not sure though
https://codeforces.com/blog/entry/64310?#comment-482095
In my opinion, posting fast such editorials without tutorials of some task is muuuch better
It gives time for problemsetter to write missing ones clearly and others an oportunity to read available parts and try to understand them
in problem c " The task is to connect some of them into ordered pairs so that each bracket sequence occurs in at most one pair and the concatenation of the bracket sequences in each pair is a correct bracket sequence". Can someone explain me the solution of c in context of the bold statement above.if we want each bracket sequence occur in at most one pair then how is the editorial solution is correct. for ex if sequences given are : "((,)),)())" then solution according to the editorial will be 1 but there will be one sequence left with no pair which violates the condition in the bold statement.Can someone clarify my doubt
At most one means zero or one.
For 1097B, how to solve it if N is bigger?
like this:47957456
it is O(nk) and can be O(nk / 32) if you use bitset
I will be glad if you make me understand these according to editorial: shanxizeng Aman_98 blitzitout
i) why should I chose 2^n-1 instead of 2^n
ii) If i-th bit is 0 so we should do it clockwise rotation for i-th, why?
In general, this is a technique for brute forcing and looking at all possible outcomes. Since, every angle has 2 options (either CW or ACW), we have at most $$$2^N$$$ possibilities. We can represent all possible outcomes in terms of binary representation of all numbers from $$$0$$$(all 0s) to $$$2^N-1$$$(all 1s). So, we can check a total of $$$2^N$$$ possibilities and see if we get the desired result.
Basically bit 0 represents one choice and bit 1 represents the leftover choice. There is no hard and fast rule, you can assign any direction to any bit. Either way it's fine.
shanxizeng Can you explain This Solution — 47957456 of yours for the problem 1097B - Petr and a Combination Lock.
I Have dried run it thoroughly but i am not able to understand the idea behind it.
Firstly,you can define h[i][j] as something that if you can get a j after rotate i time.If it's true,the value is 1,or it's 0.And you can simply get that h[i][j]=h[i-1][(j-a[i])%360] or h[i-1][(j+a[i])%360].This is a simple DP.
And then,you can define g[j]=h[i][j],f[j]=h[i-1][j].The method of calculating is similar as below.When all of the g[j] were done,you can copy g to f,and use f to calculate h[i+1].At last,you can get h[n][0].
47954506
How to solve G?
I came up with an idea that we can calculate the number of ways to choose k edge(s) from n-1 total edges, and for each way we calculate the number of the set of vertices which satisfies the condition(for every edge we chosen, there is at least one vertex(in the set) in both sides of the edge).
And that is the answer. Maybe can use DP on tree to solve it.
Because f(S)^k <--> choose k edge(s), that's equivalent.
Am I right?
sry for my poor English, wish you can understand me...
My idea is similar but not same with yours.
First we can use Stirling number to split power into several falling factorial,e.g
f(S)^k=sum{i=1...k}S(k,i)f(S)_(i),where x_(i)=x(x-1)...(x-i+1)=C(x,i)i!
then we should compute sum C(f(S),i), for every 1<=i<=k.
this is equivalent to choose i egdes and sum the number of sets valid(that means f(X) includes these edges).
then we can DP with dp(i,j) means choose j edges in i's subtree, and each egde chosen has at least one node of its subtree in the vertex set. and then the answer is dp(1,i) minus unvalid ways, the latter is only possible when (j-1) edges are all in the other's subtree(and no vertex outside this subtree is in the set). you can enumerate the "highest" edge, and the ways of this can be easily gotten use dp values.
I think problem C somehow matches to 990C - Bracket Sequences Concatenation Problem of previous codeforces contest ....
Same feeling...
yes seems same just the diffiernce is in cunting for balance strings
Could someone mind explaining to me why this solution for problem E doesn't work?
My approach is the same as described in editorial, except that I remove from list the maximum between LIS and LDS.
Unfortunately, that's just not efficient enough. That solution gives you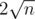 sequences, but you need around
sequences, but you need around 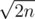 .
.
The key to the solution is that, if the LIS isn't long enough, we take the entire set of decreasing subsequences, not just the longest decreasing subsequence. Note that in general, repeatedly removing the longest/last decreasing subsequence doesn't give you the minimum cover: consider
3 0 4 2 1: you might want to take3 2 1, but the only minimal cover is3 0and4 2 1.Hmmm I'm still not fully sure I understand since at every single step I take the max between LIS and LDS, then shouldn't that mean that at least one of LDS or LIS should have size bigger K, for the case mentioned my code would work since if it takes 321 as LDS, then it would find 04 as LIS on the next step.
I don't have a case on hand which breaks it. Unfortunately, it's not true that either the LDS or the LIS has size at least K: see the sequence
3 6 9 2 5 8 1 4 7: both the LIS and LDS have size 3, but K = 4.But in that case 3 is fine, because its length is 9, not 10 and 6 is doable in 3
For N = 9, you need to solve it using 3 sequences. N = 6 only guarantees 3 additional sequences, so 9 — 3 = 6 isn't good enough.
If you want a larger case, the corresponding sequence for N = 25 has a similar issue: you can only remove 5 vertices from
5 10 15 20 25 4 9 14 19 24 3 8 13 18 23 2 7 12 17 22 1 6 11 16 21My bad
So I get what you mean which is that in the worst case you will find that LIS and LDS are both sqrt(N), so its possible that there is some sequence where by taking sqrt(N) every time instead of sqrt(2*N) it will require more iterations :S
It just seems very hard to find such case...
I tried to find a test which breaks my solution so I ran a program which tested all 9! permutations for N=9 in my code and all of them passed with K<=3, so if there is a case that breaks it it's at least N=13...
Also, do you have any idea on how you would demonstrate that the complexity of my proposed solution is 2*sqrt(N)? I did a this very simple code, and it plots approx 2*sqrt(N), but I don't know how to demonstrate it formally:
After adding the condition if len<K grab the decreasing sequences LCS generated my code passes.
My submission failed on test 9, which had permutations of size ~25. Maybe try permutations like that?
Hey I need some explanation for problem D, how to calculate the DP states, otherwise the solution is understandable.
https://codeforces.com/blog/entry/64310?#comment-482095
Thank you very much.
Can anyone explain in problem F Inclusion-exclusion. I don't understand the moment, that (i / x) is square-free.
Solve this: https://codeforces.com/problemset/problem/803/F
Inclusion-exclusion for the problem above explained: https://codeforces.com/blog/entry/51755?#comment-356983 the formula using mobius is in the editorial (it's the same thing)
I solved it :)
Thnanks!
Er
can anyone explain how to calculate dp[k][j]? I find it hard because dont we have to calculate gcd between dp[k][j] and p^j??
May be this is my personal problem, but the value of k was misleading for me, if it was 106 imo it will be better. For this value of k I wrote dp solution without knowledge of multiplicative function and it was very close to tl (about 3s on maxtest). When I wasted a lot of time I finally wrote correct solution, but this is D on div1+div2, so such trap is not good.
Actually I was a little afraid of having TLE even with correct solution. It was O(k log^2 n) with multiplications and modules. When I checked how long it takes on maxtest (2^something) it turned out it is quick, but it's not like k could have been increased significantly ... unless you would like to require binary exponentiation of matrices ;)
Hm, actually complexity equals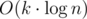 , not
, not 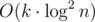
Ah yes, you're right. I mean, my code has log^2, but it is trivial to improve that, but I didn't realize since it was sufficient.
I think if you calculate with it's
it's 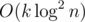 , if you calculate with
, if you calculate with 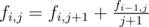 it's
it's 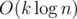 , isn't it?
, isn't it?
In problem D, can someone please explain the recurrence of the DP.
https://codeforces.com/blog/entry/64310?#comment-482095
Anyone knows of any other problem similar to problem D?
In problem F, I dont understand why operation 3 is bitiwse AND ?
If you have A[i] and B[i] multiples of i, there will be A[i] * B[i] multiples of i after taking gcd of all pairs. Also, multiplication mod 2 is &.
Thx!
Please link this editorial to contest.
Hint for G?
It's something about Stirling Numbers of the second kind.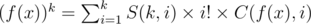 Where S(k,i) is the Stirling Number. And ... It become a DP problem. My code:https://codeforces.com/contest/1097/submission/48029930
Where S(k,i) is the Stirling Number. And ... It become a DP problem. My code:https://codeforces.com/contest/1097/submission/48029930
I wrote a tutorial of problem G. https://codeforces.com/blog/entry/64367
The first editorial is formatted so much better than the second. Thank you for both, though! :D
For problem E, how to guarantee this partition which calculates the smallest k
(Ah...I make a mistake, just forget the problem above
Perhaps irrelevant, but is there a sequence on OEIS for the term f(n) in problem E?
why in problem C, about brackets, answer is 2, but not 3?
How would you pair up the strings? I can guarantee that you only find 2 pairs, therefore the answer is 2.
like this one
"The task is to connect some of them into ordered pairs so that each bracket sequence occurs in at most one pair and the concatenation of the bracket sequences in each pair is a correct bracket sequence."
You are not allowed to combine 3 strings. So
4 6 7is not valid.sorry, I think I got it,
there it says pairs, then 3rd option is not valid
Thanks for reply.
soon™
Why are the editorials not linked with questions nowadays?
Seriously, what is the record for the latest tutorial for some problem? We're close to three weeks now.
Let me guess, Radewoosh is still enjoying the New Year, so he hasn't uploaded the editorial yet
In F,"instead of storing the parity of numbers equal to x, store the parity of numbers divisible by x." Is it divisible by X or divisors of X??
How can we solve this problem using Dynamic Programing, there is dp tag given to this problem. I am a beginner so could someone help me with this ....
which problem bro?
I am 5 years late but in B you can bitmask from 0 to (2^n)/2-1 instead of 0 to 2^n-1. all combinations from (2^n)/2-1 to (2^n)-1 are the same as the combinations from 0 to (2^n)/2-1 just different signs
can anyone explain me how are we calculating how many brackets need to be added to left of right of a bracket sequence in problem C