1102A - Integer Sequence Dividing
Tutorial
Tutorial is loading...
Solution 1
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n;
cin >> n;
n %= 4;
if (n == 0 || n == 3) {
cout << 0 << endl;
} else {
cout << 1 << endl;
}
return 0;
}
Solution 2
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n;
cin >> n;
long long sum = n * 1ll * (n + 1) / 2;
cout << (sum & 1) << endl;
return 0;
}
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, k;
cin >> n >> k;
vector<pair<int, int>> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i].first;
a[i].second = i;
}
sort(a.begin(), a.end());
vector<vector<int>> buckets(k);
vector<int> res(n);
for (int i = 0; i < n; ++i) {
buckets[i % k].push_back(a[i].first);
res[a[i].second] = i % k;
}
for (int i = 0; i < k; ++i) {
for (int j = 0; j < int(buckets[i].size()) - 1; ++j) {
if (buckets[i][j] == buckets[i][j + 1]) {
cout << "NO" << endl;
return 0;
}
}
}
cout << "YES" << endl;
for (int i = 0; i < n; ++i) {
cout << res[i] + 1 << " ";
}
cout << endl;
return 0;
}
1102C - Doors Breaking and Repairing
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, x, y;
cin >> n >> x >> y;
int cnt = 0;
for (int i = 0; i < n; ++i) {
int cur;
cin >> cur;
if (cur <= x) {
++cnt;
}
}
if (x > y) {
cout << n << endl;
} else {
cout << (cnt + 1) / 2 << endl;
}
return 0;
}
1102D - Balanced Ternary String
Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int n;
int needRep(const vector<int> &cnt, const vector<int> &need) {
int res = 0;
for (int i = 0; i < 3; ++i) {
res += abs(cnt[i] - need[i]);
}
assert(res % 2 == 0);
return res / 2;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
string s;
cin >> n >> s;
vector<int> cnt(3), cur(3, n / 3);
for (auto c : s) {
++cnt[c - '0'];
}
int need = needRep(cnt, cur);
int curRep = 0;
for (int i = 0; i < n; ++i) {
--cnt[s[i] - '0'];
for (int j = 0; j < 3; ++j) {
if (cur[j] == 0) continue;
int rep = j != s[i] - '0';
--cur[j];
if (curRep + rep + needRep(cnt, cur) == need) {
s[i] = j + '0';
curRep += rep;
break;
}
++cur[j];
}
}
cout << s << endl;
return 0;
}
Solution (PikMike)
n = int(input())
s = [ord(x) - ord('0') for x in input()]
cnt = [s.count(x) for x in [0, 1, 2]]
def forw(x):
for i in range(n):
if (cnt[x] < n // 3 and s[i] > x and cnt[s[i]] > n // 3):
cnt[x] += 1
cnt[s[i]] -= 1
s[i] = x
def back(x):
for i in range(n - 1, -1, -1):
if (cnt[x] < n // 3 and s[i] < x and cnt[s[i]] > n // 3):
cnt[x] += 1
cnt[s[i]] -= 1
s[i] = x
forw(0)
forw(1)
back(2)
back(1)
print(''.join([str(x) for x in s]))
1102E - Monotonic Renumeration
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
const int MOD = 998244353;
int main()
{
int n;
scanf("%d", &n);
vector<int> a(n);
for(int i = 0; i < n; i++)
scanf("%d", &a[i]);
map<int, int> lst;
vector<int> last_pos(n);
for(int i = n - 1; i >= 0; i--)
{
if(!lst.count(a[i]))
lst[a[i]] = i;
last_pos[i] = lst[a[i]];
}
int ans = 1;
int cur_max = -1;
for(int i = 0; i < n - 1; i++)
{
cur_max = max(cur_max, last_pos[i]);
if(cur_max == i)
ans = (2 * ans) % MOD;
}
printf("%d\n", ans);
return 0;
}
Tutorial
Tutorial is loading...
Solution 1
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
typedef long long li;
const int N = 18;
const int M = 100 * 1000 + 13;
const int INF = 1e9;
int dp[1 << N][N];
int n, m;
int a[N][M];
int mn1[N][N], mn2[N][N];
int calc(int mask, int v){
if (dp[mask][v] != -1)
return dp[mask][v];
dp[mask][v] = 0;
forn(u, n) if (v != u && ((mask >> u) & 1))
dp[mask][v] = max(dp[mask][v], min(mn1[u][v], calc(mask ^ (1 << v), u)));
return dp[mask][v];
}
int main() {
scanf("%d%d", &n, &m);
forn(i, n) forn(j, m)
scanf("%d", &a[i][j]);
forn(i, n) forn(j, n){
int val = INF;
forn(k, m)
val = min(val, abs(a[i][k] - a[j][k]));
mn1[i][j] = val;
val = INF;
forn(k, m - 1)
val = min(val, abs(a[i][k] - a[j][k + 1]));
mn2[i][j] = val;
}
int ans = 0;
forn(i, n){
memset(dp, -1, sizeof(dp));
forn(j, n)
dp[1 << j][j] = (j == i ? INF : 0);
forn(j, n)
ans = max(ans, min(mn2[j][i], calc((1 << n) - 1, j)));
}
printf("%d\n", ans);
}
Solution 2
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int N = 18;
const int M = 100 * 1000 + 13;
const int INF = 1e9;
int used[1 << N];
char dp[1 << N];
int g[1 << N];
int n, m;
int a[N][M];
int mn1[N][N], mn2[N][N];
bool calc(int mask){
if (dp[mask] != -1)
return dp[mask];
used[mask] = 0;
dp[mask] = 0;
forn(i, n){
if (!((mask >> i) & 1))
continue;
if (!calc(mask ^ (1 << i)))
continue;
if (!(used[mask ^ (1 << i)] & g[i]))
continue;
used[mask] |= (1 << i);
dp[mask] = 1;
}
return dp[mask];
}
bool check(int k){
forn(i, n){
g[i] = 0;
forn(j, n)
g[i] |= (1 << j) * (mn1[j][i] >= k);
}
forn(i, n){
memset(dp, -1, sizeof(dp));
forn(j, n){
dp[1 << j] = (j == i);
used[1 << j] = (1 << j);
}
calc((1 << n) - 1);
forn(j, n) if (mn2[j][i] >= k && ((used[(1 << n) - 1] >> j) & 1))
return true;
}
return false;
}
int main() {
scanf("%d%d", &n, &m);
forn(i, n) forn(j, m)
scanf("%d", &a[i][j]);
forn(i, n) forn(j, n){
int val = INF;
forn(k, m)
val = min(val, abs(a[i][k] - a[j][k]));
mn1[i][j] = val;
val = INF;
forn(k, m - 1)
val = min(val, abs(a[i][k] - a[j][k + 1]));
mn2[i][j] = val;
}
int l = 0, r = INF;
while (l < r - 1){
int m = (l + r) / 2;
if (check(m))
l = m;
else
r = m;
}
printf("%d\n", check(r) ? r : l);
}











Hey awoo , can you explain your solution for D ? I was thinking on similar lines but messed it up in placing 1's.
I thought of it the following way. You start with either a single amount greater than or a single amount less than
or a single amount less than  (the both zeros case is trivial).
(the both zeros case is trivial).
Case 1: Replace some of characters x with other characters. I just assumed that if the character to replace with is smaller than x then you should replace some prefix of x occurrences and if it's greater than x then suffix of occurrences. It should be easy to prove. Then the order of applying functions matters only if x = 0 or x = 2 (determining the order is trivial).
Case 2: Replace some character with character x. Following the same ideas you also determine when prefix/suffix is the best and the order of application.
The code itself is really self-explanatory. I believe that the proof is the hardest part of it.
Hey vovuh , can you explain about E? What are the possible answers for 4 1 3 3 7
There should be only three 3 closed subsegments. So answer = 2^2 = 4 But possible arrays for b is - 0 0 0 0 - 0 0 0 1 - 0 1 1 1 I can't think of the fourth answer as 0 1 1 0 can't be the answer Thanks in advance:)
0 1 1 2
Thanks:) Got it So can we say that if there are m subsegments. Then answer will be 2^(m-1), Because left most subsegments have the value 0 and all other subsegments have two options either have value of their left subsegment or increase previous value by 1 Is it correct
Yup. Correct
Shouldn't the answer be 8 (2^3) because there are four closed segments ( [4], [1], [3,3], [7])
The eight renumerations are as follows :
0 0 0 0 0
0 0 0 0 1
0 0 1 1 1
0 0 1 1 2
0 1 1 1 1
0 1 1 1 2
0 1 2 2 2
0 1 2 2 3
4 is the size of array 'a' . Not the number
Oh Sorry. My bad
We can also have another approach for Problem B (1102B - Array K-Coloring), which is also quite nice, and runs only in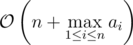 time complexity.
time complexity.
First of all, obviously if any value x exists more than k times, then there will be no coloring scenarios possible.
We'll traverse the array linearly from left to right, and color an element right after traversing it.
Let's initiate an array cnt storing the frequency of elements, a.k.a. cnt[i] is the number of elements with value i found so far.
Also, let's denote Max as the maximum index of any used colors. Initially Max = 0.
For each i (1 ≤ i ≤ n), we'll do the following:
Since this solution depends on the value of elements in a, so in case they're huge integers (maybe Int64 or such), we can use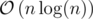 .
.
mapdata structure to implement cnt array — the complexity would beThe explanation seems long, but the it's mainly my explanation and proof for it. The implementation itself is pretty neat if you might ask. You can see it here: 48189557
P/s: I realized this comment of mine is longer than the source code itself :D
This Div 3 contest was quite interesting.
My code to D does a little more work than the editorial solution but I think my explanation might be a little easier to understand. :)
I solved it using these steps link.
nice approach
Thanks a lot for sharing your approach and solution. It made it look very simple.
You're most welcome. :)
Anyone help me to find the error in problem D? Why my solution 48190526 is getting WA in TC 13.
I think that my solution for E is a little bit easier to understand 48143299
1) a[i] == a[j] <=> b[i] == b[j] We can notice that our b value cannot become less with index increase, so if we are between two equal numbers, we can't increment our function value, because when we will come to this number (which is equal for our first number), we can't support a[i] == a[j] <=> b[i] == b[j].
So, we simply find the first and the last occurrences for every number in a[] (occur[n] = {first_oc, last_oc})
ans = 1 (because we can always make b[] = [0] * n);
Let's keep in memory value named depth, which will represent enclosure rate (just like in bracket sequences)
Simply iterate from 0 to n — 1:
if occur[N].first == i: depth++;
if occur[N].second == i: depth--;
if our depth is zero, we can put b[i + 1] = b[i] or b[i + 1] = b[i] + 1, so our ans become doubled.
I think that my explanation is incomprehensible, so you can check out the code! 48143299
In solution 1 of F, how do you ensure that the Hamiltonian path starts with i? I can see that you have changed the initial values in the DP for that but I am still not able to understand that. Can you please explain a bit?
I just make it overly unoptimal to start from any other vertex. That way any path that could have made the overall answer better will start from the vertex I want.
Where i can read about Hamiltonian path?
here
Thanks)
Could somebody please help me figure out why my O(n) solution is getting TLE for E? https://codeforces.com/contest/1102/submission/48244158
Try using 'set' instead of 'unordered_set'. I had the exact same problem of getting stuck on test 48 and changing to 'set' solved the issue. It seems that this particular test is a anti-hashing testcase made to stop people who used 'unordered_set' in their code. Relevant: https://codeforces.com/blog/entry/62393
for the problem F's first solution, can any one explain why the initialization is dp[1 << j][j] = (j == i ? INF : 0); instead of dp[1 << j][j] = (j == i ? 0 : INF); As we assume the i is the starting point, then any other node except i should be initialized to INF?
Yes, i is the starting point. But we are looking for the minimum weight of the Hamilton cycle. Setting
dp[1 << j][j](j != i) to 0 means that, the minimum weight for the other starting points are already 0, so that functioncalcwon't consider them anymore.And INF is the normal initialization, since we are looking for minimum weight and in status
1 << i, there is only one pointiand no edge (weight) has appeared.In F, solution1, what is the significance of
forn(j, n) dp[1 << j][j] = (j == i ? INF : 0);
in the main function's last nested for loop?
It ensures that path starts with i.
vovuh I have completely understood solution 1. But got stuck in solution 2. can you please explain what array dp ,used, g and function check and calc are doing in 1102F — Elongated Matrix SOLUTON2
The second solution of F can be optimised to O(2^n . n. log(MAXN))
As it is possible to check for hamiltonian path in O(2^n . n) time
https://codeforces.com/blog/entry/337