Continuing with the theme from last time, here's a quick writeup of my approaches:
1107A - Digits Sequence Dividing
Since we just want to make two numbers such that the first number is smaller than the second, our best bet is to use only the first digit for the first number and the rest of the digits for the second number. Note that since the numbers can have up to 300 digits we shouldn't actually evaluate the second number. Instead, since the digits only include 1 through 9, we can handle that case by checking the number of digits. Code: 49002957
1107B - Digital root
The key observation is that the digital root of an integer k is the single-digit number 1 ≤ d ≤ 9 such that 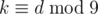 . You can prove this by noticing that
. You can prove this by noticing that 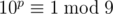 for all p. Once we observe this, finding the k-th number is very simple; see the code: 48993705
for all p. Once we observe this, finding the k-th number is very simple; see the code: 48993705
1107C - Brutality
Since we are only allowed to push the same button k times in a row, let's do a two-pointer sweep to find all segments of consisting of just one button. Within each segment, we'll sort and take the k highest values. See the code for details on the two-pointer sweep: 48994498
1107D - Compression
After some tinkering with the given condition, we notice that an x-compression is possible iff x divides n and the n × n matrix is divisible into x × x matrices such that each matrix is either all 1 or all 0. We can loop over all such x and check the condition in n2 time per x, but this is potentially too slow.
To speed this up, we can precompute rectangle sums for every rectangle containing the upper-left corner, which enables us to compute the sum of any rectangle in  . This improves our time complexity to
. This improves our time complexity to 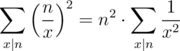 . Since
. Since 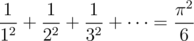 (really!), this means our solution is
(really!), this means our solution is 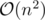 . Code: 49028814
. Code: 49028814
1107E - Vasya and Binary String
We set up a DP on (start index, end index, number of consecutive digits matching our start index). In other words, the current string we are solving is the substring from start index to end index, plus some number of additional digits (all equal to S[start]) added as a prefix to our substring.
We then have two choices from any given state:
- Cash in on our consecutive digits at the start and recurse on
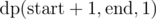 .
. - Pick an index i such that S[start] = S[i], and collapse everything between those two indices in order to merge them together for an even larger prefix. This results in a score of
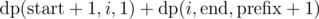 , and we can loop over all i to take the maximum.
, and we can loop over all i to take the maximum.
The runtime is 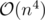 , with a very good constant factor. Code: 49036191
, with a very good constant factor. Code: 49036191
Does anybody have  ?
?
1107F - Vasya and Endless Credits
Notice that if we take offer i exactly m months before we buy the car, it will provide us with 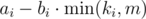 money at the time of the car purchase. Moreover, the only values of m that make sense are 0 ≤ m ≤ n - 1. This means we can immediately solve the problem via an algorithm for the assignment problem, such as min-cost flow or the Hungarian algorithm. This has a runtime of
money at the time of the car purchase. Moreover, the only values of m that make sense are 0 ≤ m ≤ n - 1. This means we can immediately solve the problem via an algorithm for the assignment problem, such as min-cost flow or the Hungarian algorithm. This has a runtime of 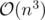 or
or 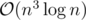 , which manages to fit under the time limit with a good implementation. Code: 49033783
, which manages to fit under the time limit with a good implementation. Code: 49033783
The better solution is to notice that for all offers i where we don't use up all ki months, it's best to sort them by bi (so that the highest values of bi have the lowest values of m). This leads to a very nice 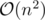 DP solution: 49035446
DP solution: 49035446
1107G - Vasya and Maximum Profit
We can first compute all values of 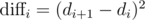 . Since we only care about the maximum such value within our segment, we can use div-conquer to solve every segment. In particular, if we know the index of the maximum value in
. Since we only care about the maximum such value within our segment, we can use div-conquer to solve every segment. In particular, if we know the index of the maximum value in 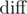 , we know that any segment crossing this index has this value as its maximum. We can thus solve all segments crossing this maximum and recurse on the left and right sides.
, we know that any segment crossing this index has this value as its maximum. We can thus solve all segments crossing this maximum and recurse on the left and right sides.
To find the best crossing segment, note that each problem contributes a value of a - ci. We can independently find the largest sum starting from our crossing index going left and the largest sum going right, and add these two together for the best overall crossing segment.
Unfortunately, since we can't guarantee that the maximum indices will divide our interval nicely in half, this does not lead to the usual 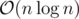 runtime of div-conquer but is instead
runtime of div-conquer but is instead 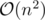 in the worst case. To improve on this, we can precompute partial sums of a - ci and use RMQ to find the minimum sum left of the crossing index and the maximum sum right of the crossing index. This reduces the crossing computation from
in the worst case. To improve on this, we can precompute partial sums of a - ci and use RMQ to find the minimum sum left of the crossing index and the maximum sum right of the crossing index. This reduces the crossing computation from 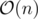 per index to
per index to 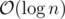 or
or 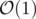 , giving an overall runtime of
, giving an overall runtime of 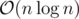 . Code: 49036431
. Code: 49036431











For D, I think I had a slightly simpler solution. For every row find the gcd of the lengths of continuous patches of 1 and continuous patches of 0. Do this for each row and for each columns and take GCD of all these numbers and that will be the answer. To do this you just need to traverse the matrix twice.
Nice, that works as well and should also be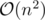 .
.
can you please explain what needs to be done in problem D?
lets A= 1111 1111 0111 1111
here for x=2, A[3][1]!=X[2][1] so 2 compression is not possible right? 3/2=1.5(round to 2) 1/2=0.5(round to 1)
Am I right?
I used to think in that way.But the problem wants us to dived A into (n/x)*(n/x) squares (n%x==0) each square is x*x and for every small matrixs all the number in the matrix is the same(then we can compress it in a single number).so ans of your example is 1 because (if it is a 4*4 square, then A[3][1] is wrong , if it is 4 2*2 square ,then A[3][1]!=A[3][2]=A[4][1]=A[4][2]).if the set is 0011,0011,1100,1100 then the answer can be 2.
How does that work? Any intuition or proof behind this? Pardon me if that is something trivial, but I don't a have a clue.
easy
if value at (x,y) != value at (x+1,y) then there is a border between them (they cant be in one compressed cell) so the answer is the divisor of x
same for y
consider d-compression
then the borders are at d,2d,3d,4d...
I just check the length of every continuous identical row and calumn as well, and then take the GCD of them as the answer. I'm not sure if it is right, but it passed the judge.
i am doing the same thing but it is giving me runtime error on case 3. https://codeforces.com/contest/1107/submission/49065786 ..what is wrong in this?
Bit of necroposting, especially since you have solved this problem already, but maybe it will be helpful for you anyway to not resign from bitset in the future :)
s3[i]=s[i].substr(1300-n2,n2);
n2 is bigger than 1300, hence the error. Probably you meant to write n2/4 ("probably", not sure since I didnt dive deep into the code, just took a look).
Thanks For Your fast editorials <3 Love it man <3
My solution to C is slightly different in implementation, but the same idea. I thought it would not be correct.
Rather than use pointers to find the beginning and end of each segment,
Here is a link to my submission. Can someone please help me in calculating the time complexity of this approach ? I know it's practical enough to fit in the time limit but it's difficult to calculate the time complexity.
In Worst Case ( all elements of press are same, sorting will take nlogn ) it would be O(nLog(n)),
Best Case: O(n) ( when all 2 contiguous presses are different ) .
Why is that the worst case ?
If all presses are same (e.g. aaaaaaaaaaaaaaaaa ), your array will have all N presses so now there are N elements in array, sorting will take at least nLogn time. (c++ sort uses merge sort which take nLogn.)
I understoood that but you have to prove that that is the worst case.
In my opinion sorting the entire string is easier than stopping and sorting parts of it.
It seems to be true but actually it is not.
e.g. suppose you have 16 elements and divide that into 4 equal portion.
When you take all 16Log16 = 64
when divided 4 * ( 4Log4 ) = 16Log4 ( < 16Log16 ) = 32
( base of Log is 2 ).
Also note that dividing 16 into 16 portion will give 16 * ( 1Log1 ) = 0 but that's not true because sort complexity for 1 element will be 1. So in this scenario it will be 16 * ( 1 ) = 16.
To prove see picture. How to prove
Also note that complexity means we are talking about asymptotic complexity.
P.S. Sorry for my handwriting :)
Your handwriting is nice. I appreciate your effort ! :)
Thanks!.
For C, I find it simpler to use a priority_queue, which will store the values of the ith click, where the character for all i in the priority_queue are the same.
For example, for the string abaaaac, max clicks=3, and array a[] contains the points, when at character 'c', the priority_queue will contain a[2],a[3],a[4],a[5], and you will then pop k elements. I think the complexity is O(NlogN)
For G alternative solution is existed.
Let define segment structure which consists of sum on this segment, gap, previous segments and next segment. Structure's comparer is: what gap is needed to merge with previous segment. Segments are stored in set.
Go from left to right. After step we must add new segment with parameters: gap = (d[i] — d[i — 1]) ^ 2, sum = 2 * m — c[i] — c[i — 1]. After it we merge all segments in set, which are needed gap < current gap to merge with prev. Let's remove mergeable, prev and next for mergeable and add mergeable and next for mergeable segments to set (it's needed for updating set, comparer for next was changed).
Answer is the best answer after each merge, segment's creating, best of m — c[i] and zero. Asymptotics — O(N * log(N)).
Code: 49039327
I find another way to solve problem D with O(n^2) first,init row.(i.e. 000111000 to 3,3,3 and 00111100 to 2,4,2) second init column.(Do the same thing with init row) Third,find the GCD of all the numbers we inited. Then we get the answer.You can see it clearly in my submission:49007032.
I also did something different at G. First update the solution to the maximum if we took any individual problem. Next choose a consecutive pair of numbers (you have to go through all of these pairs) and consider their gap the maximum in this particular solution. Suppose they were (i,i+1). Next find values lo and hi such that the gap between two adjacent pairs of problems between lo and hi is not greater than (i,i+1) and lo is lowest and hi is highest. This can be done with binary search and rmq, perhaps even segtree. Compute the partial sum array pr[i] = pr[i-1]+a-c[i] which gives the profit if we chose the first i problems. Now we need the highest value in pr between i and hi and lowest between lo-1 and i-2 (we are removing the smallest prefix from our highest prefix so that we are left with the best answer) and this can be done with segtree or another rmq. Lastly update the answer and go to the next pair. I personally used BS+rmq for (lo,hi) and segtree for the partial sum, the complexity being O(n*logn) both space and time.
Source code here: http://codeforces.com/contest/1107/submission/49022063
I wrote a program that has 5 nested loops, but it still runs very fast...
It cannot be O(n5), right?
I iterated over the matrix with interval x, then, I checked each submatrix of the size x * x, If this submatrix is diverse (it has both 0s and 1s) then x is impossible to be a correct compression.
The submission → 49019600
Can someone please analyze the complexity? Thanks :D.
It seems that my solution is similar to yours...I think it is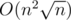
More precisely, it's O(n2σ(n)) where σ(n) is the divisor function. For n ≤ 5200, the largest value of σ(n) is 60 for n = 5040.
I think it runs faster than that. Because there is a
breakin the innermost loop. For many randomly generated tests, it is very easy to break in the first or second time.In fact,for your solution,O(n2σ(n)) is a tight upper bound...
For problem E : Is there anyone who wrote a dp bottom-up solution (as explained in the editorial) ?
You can just fill the table in increasing order of (end - start): 49056683
LeetCode 546...
For D, I noticed that O(n^2 * N) (where N denotes number of different values of x that had to be checked) solutions have also been accepted. This made me sad. :P
As we know that amount of divisors for N is about N^(1/3), we can simply iterate over all N's divisors and check if matrix can be x-compressed with x equal divisor in O(N^2). So O(N^2 * N^(1/3)) works
It is actually less than 60, according to meooow
Just a neat idea I found out for G :
Let s[i] = (d[i+1] — d[i])^2, sum[l->r] = sum(a-c[i] with i = l->r), What we are trying to do is to find a segment [l,r] that maximize:
The first part sum[l->r] is easy to handle while keep track of the second part is more difficult. So I came up with using double-ended queue to find largest l and largest r such that l<=i<= r and s[i] = max(s[j] with j = l->r) for every i = 1->n-1.
The problem turned out to be classic: We have n-1 queries, each query asks us to find out the maximum sum[i->j] with l<= i<= j<= n. This is a old Segment Tree problem (even with no update activities on the data structure), given l, r(l<=r) find the maximum consecutive sum lies within [l,r].
Just take care of 4 factors in a Node of the segment tree managing [l,r]: MAX, MAXSUMLEFT, MAXSUMRIGHT, SUM.
Oh just take care of the case when C = gap(l,r) = 0(when l==r). It is easy though
Nice solution of E! :)
for question Digital Root-B somebody please tell me why this code is running for 1 second time constraint 49002397 even though the user has run a loop till k which is 10 raise to power 12
It's one of the optimizations that g++ does as part of the
-O2flag.When the compiler sees the loop
it is actually smart enough to optimize that away into
b += 9*(a-1), therefore the code passesI had the same insight as you mentioned for DP solution of F but couldn't form a solution out of it. Could you please explain the DP solution a bit more.
So I'm back here after a while, this time with some idea of what the DP state in the solution means and the corresponding proof of correctness (not very formally tho, I believe state definition makes it sort of clear in case of DP based solutions).
Now some ground work, the solution shall have some offers that we don't pay off completely and some that we do. In an optimal ordering the relative order of these should clearly be ones paid off followed by one we didn't pay completely. Within the latter they should be ordered in decreasing order of b value, because you want to pay higher amounts fewer times. That's why the sorting. The sorting ensures that the quadratic DP solution does happen to cover the solution we need. This idea is called exchange arguments, I think.
dp[i] in neal's solution indicates the optimal value we can make given that the first offer that we don't pay off completely was taken i months before the month we decide to run off. This naturally also means that dp[i] considers a subset of the cases where we have at most i unpaid offers, more specifically the subset with one offer taken exactly i months before running off (if at all we have unpaid offers, it also covers the cases where we have 0 unpaid offers).
To avoid this complication (sort of) in the state definition, I decided to modify it a bit and write a slightly longer but easier to understand solution. In my solution dp[i] indicates the optimal value if we use at most i unpaid offers. That's it. Then we can simply return dp[n]. How do I code it ? Its very similar to neal's solution (of course!) but I've written the loop such that the updates to a particular state take place in one iteration. After I go through that iteration I go through the dp array and overwrite it with a running max, in order to follow what I think is an easier to understand state definition.
Code :- 91230696 Code2 :- 91234502
Can anyone please tell me what's wrong in my code? https://codeforces.com/contest/1107/submission/49065947
Your code that checks whether a divisor is okay or not, is wrong.
Can you point out the mistake? Thanks in advance.
I think the method itself that you are trying to use is wrong, not some small mistake. You could try something else or see how others did it.
Problem G:
For every diff[i], I calculated the range in which it is maximum and took maximum suffix from left side and maximum prefix from the right side to calculate the answer.
Before constructing the segment tree,just to verify the logic I submitted the code with O(n) function to calculate max prefix and suffix expecting a TLE, but surprisingly it got ACed.
Submission: 49068594
Are the test cases weak or is the time complexity of this solution lesser than O(n^2)
Nice observation. I did some testing and actually, since di only goes up to 109, it may not be possible to construct a test case under the problem's constraints that fail all worst-case n2 solutions of this form.
With larger constraints, it should be quite easy to break: set d1 = 1, d2 = 1 + 2, d3 = 1 + 2 + 3, ...,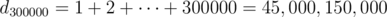 . Then
. Then 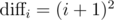 is a strictly increasing sequence.
is a strictly increasing sequence.
Of course, now you run into the problem that di2 overflows long long, which I assume is why the problem setters didn't increase the constraint further.
With that solution u may not even have calculate function and just go from index i while u can :)
Can someone explain how DSU can be used to solve Problem D? Example Submission
Can someone please explain the reason behind each matrix being either all 0 or 1 in question D ?
For problem F,the dp solution: dp[i + 1] = max(dp[i + 1], dp[i] + off.A — i * off.B); dp[i] = max(dp[i], dp[i] + off.A — off.K * off.B); I don't understand this two lines. Who understand it and please tell me.
I have tried to solve problem G in a simple way. But it's giving wrong answer verdict on test 7.Can someone please find the error in logic in my code?
https://codeforces.com/contest/1107/submission/49040214
Thanks in advance!
If you have done Kadanes algo then it's wrong because if you take positive profit and neglect negative profit ,then negative might become positive in future because of different max gap..
I think problem G can also be solved using the classic divide-and-conquer method. To get the answer in a range [l, r], we let mid = (l + r) / 2 and analyze two cases: the segment contains mid or not. For the latter one, we can solve recursively.
To find out the answer for the former case, we compute the cost and max(di + 1 - di)2 for each prefix/suffix spanning from mid. Then we need to combine the prefixes/suffixes to get the optimal answer. This can be done with the scanline technique, which is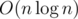 due to the sorting, and the overall complexity is
due to the sorting, and the overall complexity is 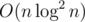 .
.
However, one can easily observe that max(di + 1 - di)2 for the prefix/suffix is already sorted, thus the problem can be solved in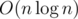 .
.
Code: 49522292
very clear solution.
I am not able to get the intuition for problem E. Can anyone explain DP states and transition in simpler terms?
I can't get the meaning behind the state of dp[i] in problem F, can someone help me?
+1
And the proof of its correctness??
Not very formal, but here you go.
+1, not really sure the correctness.
For D we can also check if it can be compressed into squares of size s, where s can be a prime divisor or a power of a prime divisor and then we multiply those that fulfill the condition to obtain the answer.
For instance, if n = 2^5 * 3^2 * 5, we can check the following: 2, 2^2, 2^3, 2^4 and 2^5 and get the greatest value among them (or 1 if none). 3, 3^2 and get the greatest value among them (or 1 if none). 5 and if it doesn't fulfill, then we take 1.
And finally we multiply those numbers to obtain our answer. This is correct because for instance if our array can be compressed into 2 or 3 size squares, then if we have a look on the top left 6 * 6 square we can see that the first 3 rows must have the same numbers (let's say 0) and thus the 2nd 2 * 2 square must also consist of only 0s, hence 4th row is 0 and therefore the 2nd 3rd square must have the same form. Therefore, we deduce that the top left 6 * 6 must be a compression. We can use similar reasoning for any other square as well as for any other two co-prime numbers whose squares are a valid compression.
We can see that we can perform at most 12 checks (2^12 = 4096 < 5200, the limit).
what if for 1107A — Digits Sequence Dividing if we have to divide it into maximum partitions ?
For Problem G: I used Kadane's algorithm but it gives wrong answer on test 7 and test 36 only. Could anyone point out the issue with this approach. Code with some comments.
problem b can someone explain me how we got that logic k=d%9