| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
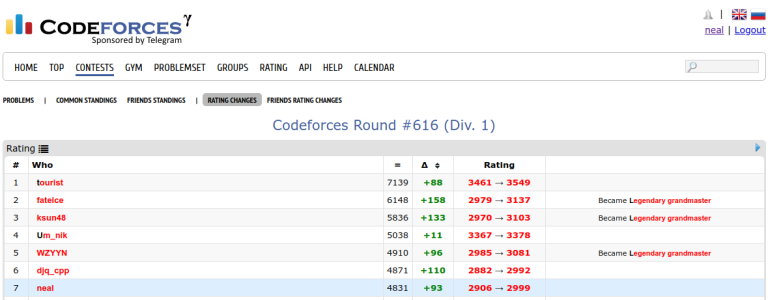
After making several submissions earlier today to 1463F - Max Correct Set that all involved calling clock(), I think I've found some major inconsistencies in clock timing on Codeforces.
I had a solution that was correct but borderline on runtime because it needs to generate enough data to extrapolate from (via Berlekamp-Massey). So I made it iterate until 3.8 seconds, and looking through the submission list, it appears I wasn't the only one with this type of idea. Unfortunately I got WA on several submissions: 101579005 101581695 101583625. The strange thing was that each test case that resulted in WA didn't actually run for the full 3.8s, but only about half of that. When I took the same code and ran it in custom invocation with the same input, it used the full 3.8 seconds and got the right answer each time.
So what's going on here? To try to figure this out, I set up a simpler version of some timed code since the submissions above are quite complicated. Here's what I've got now. This uses multiple different methods of timing, including clock(), wall time, and std::chrono::steady_clock. It also calculates a sum via a loop as kind of a proxy for "how much work" is actually being done.
#include <chrono>
#include <iostream>
#include <sys/time.h>
using namespace std;
long double wall_time() {
timeval tv;
gettimeofday(&tv, nullptr);
return tv.tv_sec + tv.tv_usec * 1e-6L;
}
const double TIME_CUTOFF = 1.0;
const int ITERATIONS = 1e6;
int main() {
long double clock_begin = clock();
long double wall_begin = wall_time();
auto chrono_begin = chrono::steady_clock::now();
int64_t sum = 0;
while ((clock() - clock_begin) / CLOCKS_PER_SEC < TIME_CUTOFF) {
for (int iter = 0; iter < ITERATIONS; iter++)
sum += iter % 3;
}
cout << "clock: " << (clock() - clock_begin) / CLOCKS_PER_SEC << 's' << endl;
cout << "wall: " << wall_time() - wall_begin << 's' << endl;
cout << "chrono: " << 1e-6L * chrono::duration_cast<chrono::microseconds>(chrono::steady_clock::now() - chrono_begin).count() << 's' << endl;
cout << "sum = " << sum << endl;
}
Most of the time you get an output you would expect, like either of the two outputs below:
clock: 1.006s
wall: 1.0058s
chrono: 1.00603s
sum = 1335998664
=====
Used: 1014 ms, 12 KB
clock: 1.008s
wall: 1.0082s
chrono: 0.979013s
sum = 1311998688
=====
Used: 998 ms, 4 KB
Very close to 1 second of runtime and about 1.3 billion loop iterations (computers are pretty fast!). But around 1 out of every 10 runs, you end up with something like this instead:
clock: 1.015s
wall: 1.0152s
chrono: 0.986539s
sum = 656999343
=====
Used: 483 ms, 4 KB
Or this:
clock: 1.01s
wall: 1.0108s
chrono: 0.981722s
sum = 653999346
=====
Used: 514 ms, 4 KB
(You can try this out for yourself in custom invocation. Make sure you change the input on the right side each time, because Codeforces caches the output when given the same input.)
This is very weird -- clock(), wall time, and chrono::steady_clock all agree here that the runtime has been 1 second, but Codeforces only outputs about half of that. On top of that, the actual sum outputted is also right around half, so the code is actually only doing half as much work. What's happening?
My best hypothesis for this now (warning: lots of speculation here; also shoutout to AnandOza for discussing) is that a small number of the Codeforces judges are older machines that run about 2x slower than the main machines. As a result CF implicitly gives twice as long of a time limit on these machines, so when 1 second of actual CPU time has passed on these machines, you have only used "0.5 seconds" of your time limit, and you've only done half of the amount of work you'd expect to be able to do in 1 second. This idea lines up neatly with the "Attention" notices on old problems that runtime is reported back doubled (e.g., see the top-right of 1C - Ancient Berland Circus).
Is there any workaround for this? Perhaps at least a way to be able to tell which of the two situations we're in? I think there are legitimate use cases for this, such as Berlekamp-Massey as above, randomized algorithms for constructive problems, or randomized algorithms which reduce the probability of error with each iteration. It would be unfortunate if these solutions didn't have a consistent method to tell time and ended up failing because of this random unpredictable factor.
Hi all, I just uploaded two videos to YouTube for today's Round #686 (Div. 3):
I finally got AC on problem G from Edu Round 98 earlier today. The editorial mentions centroid decomposition to get a runtime of $$$n \log^2 n$$$ or $$$n \log n$$$, but I actually had a completely different algorithm and I'm not 100% sure of the time complexity.
Like the editorial, my first idea was to compute the distances for each vertex to the closest of Bob's vertices using multi-source BFS. Then my goal is to iterate each vertex $$$v$$$, and for every vertex $$$u$$$ whose distance from $$$v$$$ is at most bob_distance[v] - 1, update answers[u] to be at least bob_distance[v].
Doing this directly via DFS is correct but obviously gets TLE, e.g., 99053280. I initially thought we could iterate $$$v$$$ in decreasing order of bob_distance[v] and stop the DFS anytime we reach a node that already has an answer. But this is incorrect because there can be cases where a smaller distance node reaches farther in some direction than a larger distance node.
Instead, by adding a key optimization to track the remaining steps we can still take from our current node and only continue the DFS when we strictly increase the maximum value of remaining this node has seen, the algorithm is correct and gets AC: 99053359.
I suspect this algorithm is $$$n \sqrt n$$$ in runtime. (I have a specific case where it takes $$$n \sqrt n$$$ steps to finish). Can anyone prove this runtime as an upper bound?
Hey Codeforces, quick note that I'll be doing a post-contest stream for Edu Round 98 immediately after the round ends. Planning to discuss what everyone thought of the round and share my approaches to the problems.
You can find my stream at https://www.twitch.tv/nealwu. Hope to see you there!
Update: YouTube link for the screencast and link for the stream.
Hey everyone, here's my screencast of Kickstart Round H which just finished. I also added commentary and explanations for each of the problems--let me know if this is helpful!
Hi Codeforces! I'll be doing my first stream ever in just under 45 minutes from now.
I'm planning to virtual Round #676 (Div. 2) and discuss the problems along the way; it should be pretty casual. The stream will be at https://www.twitch.tv/nealwu. Hope to see you there!
UPDATE: this stream and the stream after are now on YouTube.
Here are my approaches to the problems today:
1418A - Buying Torches
Since the second trade is the only way to get coal, we clearly need to perform the second trade $$$k$$$ times. So how many times do we need to do the first trade? We can see that in order to end up with enough sticks and coal by the end, we need to obtain $$$ky + k$$$ sticks ($$$ky$$$ to convert to coal and $$$k$$$ to save as sticks). Since the first trade really just gives us $$$x - 1$$$ new sticks each time, we'll need to make $$$\displaystyle \left \lceil \frac{ky + k - 1}{x - 1} \right \rceil$$$ first trades (reference to floor and ceiling functions for anyone unfamiliar).
For implementation details, note that for positive integers $$$a$$$ and $$$b$$$, $$$\displaystyle \left \lceil \frac{a}{b} \right \rceil = \left \lfloor \frac{a + b - 1}{b} \right \rfloor$$$. Code: 92851684
1418B - Negative Prefixes
We can think about the problem as follows: we want to order the $$$a_i$$$ to create the longest possible nonnegative prefix of $$$p_n, p_{n - 1}, \dots, p_1$$$ (in other words, the smallest possible $$$k$$$ such that $$$p_n \geq 0, p_{n - 1} \geq 0, \dots, p_k \geq 0$$$).
Notice that $$$p_n = a_1 + \dots + a_n$$$ is fixed. We can also see $$$p_{n - 1} = p_n - a_n$$$, $$$p_{n - 2} = p_n - a_n - a_{n - 1}$$$, etc. So we should make $$$a_n$$$ as small as possible (assuming it is unlocked), then $$$a_{n - 1}$$$, and so on. In other words the unlocked $$$a_i$$$ should be sorted in decreasing order from left to right. To prove this, you can use an exchange argument: if you consider an arrangement of the $$$a_i$$$ where two consecutive unlocked values are not in decreasing order, we can swap them with each other. This swap does not make any of the $$$p_i$$$ smaller (it can only make some $$$p_i$$$ bigger). Thus we can start with the optimal ordering and repeatedly apply swaps until the unlocked values are sorted, without making anything worse.
Code: 92797816
1418C - Mortal Kombat Tower
This is a DP where the state is the prefix of the bosses we've fought and the person whose turn it is next; the DP value is the number of hard bosses our friend had to fight, which we want to minimize. For each state we can simply consider both options of fighting one boss or fighting two bosses to progress to a future state.
See the code for details: 92798564. In this solution, dp[i][who] represents the minimum number of hard bosses for our friend given that we've finished the first i bosses and that it is who's turn to go next (0 is us, 1 is our friend). In the code I use a little trick that who * hard cancels out the hard bosses for us but includes them for our friend.
1418D - Trash Problem
Note that we can move multiple piles together at the same cost as moving a single pile. This means that if we have a group of piles we want to collect together, as long as we bring them together somewhere between min(x_i) and max(x_i), the cost of doing this will be max(x_i) - min(x_i).
In particular, since we can end up with two piles, we'll want to create two segments like the following in order to collect everything (* means pile, — means segment):
*----*-*-------* *-----*---*
We want to minimize the combined length of the segments, but notice that this combined length is equal to max(x_i) - min(x_i) - the gap in between the segments. So we just need to maximize the gap, by taking the maximum value of $$$x_{i + 1} - x_i$$$.
In order to do this and handle queries, we can store all of the positions in a set and all of the gaps in a multiset. Then when we add/erase a position $$$x_i$$$, we only have to adjust three gaps: $$$x_{i + 1} - x_i$$$, $$$x_i - x_{i - 1}$$$, and $$$x_{i + 1} - x_{i - 1}$$$.
Code: 92847621. Be careful that when erasing from a multiset, ms.erase(key) removes ALL occurrences of key from the multiset. Instead, we want ms.erase(ms.find(key)).
1418E - Expected Damage
Given $$$a$$$ and $$$b$$$, let's define big monsters as monsters with $$$d \geq b$$$, and small monsters as monsters with $$$d < b$$$. We will only take damage from monsters that come after the $$$a$$$-th big monster. In particular, if $$$a$$$ is larger than $$$big$$$ (the number of big monsters), we know the answer is immediately 0.
Otherwise, every big monster has a $$$\displaystyle 1 - \frac{a}{big}$$$ chance of doing damage (the chance it is not one of the first $$$a$$$ big monsters). For small monsters, they are equally likely to be in any of the $$$big + 1$$$ gaps before/between/after the big monsters. In the first $$$a$$$ gaps, they will not do any damage, and after that they will. So each small monster has a $$$\displaystyle 1 - \frac{a}{big + 1}$$$ chance of doing damage.
So the answer we want is $$$\displaystyle 1 - \frac{a}{big}$$$ times the sum of every big monster, plus $$$\displaystyle 1 - \frac{a}{big + 1}$$$ times the sum of every small monster. We can use prefix sums to quickly get the sum of all small monsters / all big monsters for each query. Code: 92809090
1418F - Equal Product
Given a particular value for $$$x_1$$$, we can determine the range of $$$y_1$$$ that would be valid based on the two constraints $$$1 \leq y_1 \leq m$$$ and $$$\displaystyle \frac{L}{x_1} \leq y_1 \leq \frac{R}{x_1}$$$. Let's call it $$$[y_{low}, y_{high}]$$$.
Let's say there exists a valid $$$(x_2, y_2)$$$ that fits the desired constraints such that $$$x_1 y_1 = x_2 y_2$$$. Then if we write $$$\displaystyle \frac{x_2}{x_1} = \frac{a}{b}$$$ as a reduced fraction, we must have that $$$a > b$$$ and that $$$b$$$ is a factor of $$$x_1$$$. Moreover, since $$$x_1 y_1 = x_2 y_2$$$ means that $$$\displaystyle \frac{y_1}{y_2} = \frac{a}{b}$$$, we must also have that $$$a$$$ is a factor of $$$y_1$$$.
If given $$$x_1$$$ we can find $$$y_1$$$, $$$a$$$, and $$$b$$$ that satisfy the above constraints, we are almost done. The only remaining constraint is to ensure that $$$\displaystyle x_2 = x_1 \frac{a}{b} \leq n$$$. So in particular, given values for $$$x_1$$$ and $$$b$$$ (such that $$$b$$$ is a factor of $$$x_1$$$), we want to find the smallest value of $$$a$$$ such that $$$a > b$$$ and $$$a$$$ is a factor of at least one number in our desired $$$y$$$-range $$$[y_{low}, y_{high}]$$$.
In-contest, I then found two separate algorithms that should be fast in different scenarios and decided to use whichever of the two I guessed to be faster for each value of $$$x_1$$$. The first algorithm is to iterate all of the factors of $$$x_1$$$ as $$$b$$$ and find all of the corresponding valid choices for $$$a$$$. Then loop up those choices for $$$a$$$ from smallest to largest, and for each it just takes a quick O(1) check to determine whether any number in $$$[y_{low}, y_{high}]$$$ is divisible by $$$a$$$. This has a worst case of $$$O(n)$$$ per $$$x_1$$$ but often returns early (as soon as it finds a solution).
In most cases where the first algorithm takes a long time, it's due to the range $$$[y_{low}, y_{high}]$$$ being very narrow. In this case, a separate algortihm is possible by iterating $$$y$$$ from $$$y_{low}$$$ to $$$y_{high}$$$, then iterating the factors of $$$y$$$ as $$$a$$$, and then checking whether an appropriate value for $$$b$$$ exists among the factors of $$$x_1$$$.
This was able to pass the tests in about half of the time limit: 92840659. I don't have a solid proof for the efficiency of this solution though. Maybe someone can find a way to hack it?
Instead by using a segment tree, you can end up with a clean $$$O((n + m) \log^2 m)$$$ solution. The main idea is that since $$$y_{low}$$$ and $$$y_{high}$$$ are bounded by $$$[1, m]$$$, we are really doing a 2D range query on $$$y_{low}$$$, $$$y_{high}$$$, and $$$b$$$ where we want to find the smallest factor $$$a$$$ of any $$$y$$$ in $$$[y_{low}, y_{high}]$$$ such that $$$a > b$$$. We can do a sweep on $$$a$$$ and $$$b$$$ instead to just handle these queries with a 1D seg tree instead (query minimum in range, update individual element). See the code for more details: 92847130
1418G - Three Occurrences
First let's try to count the number of subarrays where the number of times every integer occurs is a multiple of 3. We can think about creating a 'signature' for each prefix of the array, where the signature tells us how many times each value $$$a$$$ occurs in the prefix of the array, modulo 3. So if the prefix is [3, 2, 1, 2, 2], our signature should be [1, 0, 1], since 1 occurs once, 2 occurs three times (0 mod 3), and 3 occurs once.
Now a subarray satisfies our condition iff the prefix for its start and the prefix for its end have the same signature. But we don't have time to actually store every signature, so instead we'll compute a hash of every signature and count equal pairs using a hash map.
We need a hash which we can update quickly after updating a single element. One obvious option is the polynomial string hash, but there's something even better: generate a random 64-bit number for every index random[i], and then we define our hash as the sum of freq[i] * random[i] where freq[i] is in {0, 1, 2}. We can show that if two frequency arrays are different, their hashes collide with probability at most $$$\frac{1}{2^{63}}$$$.
Now the only thing left to handle is the "exactly thrice" condition. The way we do this is by iterating over the end point from left to right and keeping track of the last three locations of every value. We can then ensure that we only consider start points that are large enough so that our subarray will never contain more than three of any value. To remove invalid prefixes, we can simply subtract them out from our hash map. The final solution is very short and $$$O(n)$$$: 92855419
Congrats to all of the top 25:
- Um_nik
- Benq
- Radewoosh
- Geothermal
- PavelKunyavskiy
- ecnerwala
- Petr
- maroonrk
- neal
- tourist
- 300iq
- ksun48
- molamola.
- scott_wu
- Errichto
- stevenkplus
- never_giveup
- ko_osaga
- pashka
- geniucos
- hitonanode
- Alex_2oo8
- budalnik
- snuke
- dacin21
Fun fact: everyone on this list is an IGM or higher!
Haven't done one of these for a while! Here are my approaches to the problems:
1400A - String Similarity
We just need to make sure our string of $$$n$$$ characters matches each of the $$$n$$$ substrings in at least one spot. The easiest way to do this is to take every other character from $$$s$$$. Code: 90908018
Another fun solution: we can generate random strings and check them until we find one that matches everything. This works because the probability of failing to match any particular substring is $$$\frac{1}{2^n}$$$, so as $$$n$$$ gets bigger the probability of failing gets extremely low. Code: 90999219
1400B - RPG Protagonist
First iterate on the number of swords we will personally take. Then we should greedily take as many war axes as we can until we run out of money. At this point, our follower needs to take as many items as possible. They can do this by greedily taking whichever of swords or war axes are cheaper until they run out, followed by taking the more expensive of the two. Code: 90918673
1400C - Binary String Reconstruction
Note that $$$s_i = 1$$$ means "either $$$w_{i - x} = 1$$$ or $$$w_{i + x} = 1$$$," whereas $$$s_i = 0$$$ means "both $$$w_{i - x} = 0$$$ and $$$w_{i + x} = 0$$$." We can greedily solve this by starting out our string $$$w$$$ with all 1's, then marking $$$i - x$$$ and $$$i + x$$$ as 0 whenever we are forced to because $$$s_i = 0$$$. Then we can simply check whether all of the $$$s_i = 1$$$ conditions are valid to confirm. Code: 90915688
1400D - Zigzags
We can rethink this as counting the number of equal pairs $$$(a_i, a_j) = (a_k, a_l)$$$ where $$$i < j < k < l$$$. To do this we loop over $$$j$$$ from right to left and make sure we have all $$$(a_k, a_l)$$$ pairs where $$$k > j$$$ counted in a map. Then we simply iterate over $$$i$$$ and add up the number of occurrences of each $$$(a_i, a_j)$$$ in the map.
For implementation details, note that we don't actually want to use a map and make our code slower. We can just use an array of size $$$n^2$$$ and convert the pair $$$(a_i, a_j)$$$ to the number $$$a_i \cdot n + a_j$$$ since the $$$a_i$$$ are in the range $$$[1, n]$$$. As a bonus, even if the $$$a_i$$$ were larger than $$$n$$$, we could just compress them down to $$$[1, n]$$$ and repeat the solution above. Code: 91019003
1400E - Clear the Multiset
Notice that we can reorder the operations in any way we want without affecting the result. So let's do all of the first-type operations before the second-type operations. Then it's clear that the number of second-type operations we'll need is the number of nonzero elements left over after the first-type operations. So we just want to choose first-type operations to minimize the number of first-type operations plus the number of nonzero elements left after we're done.
Let's say we have an array $$$a$$$ where $$$a_m$$$ is the minimum value (if there is a tie, you can pick any tied index). I only have a messy proof for this at the moment, but it turns out we only need to consider two options: either take all $$$n$$$ second-type operations, or use $$$a_m$$$ first-type operations on the entire array and then recursively solve $$$a_1 - a_m, ..., a_{m - 1} - a_m$$$ and $$$a_{m + 1} - a_m, ..., a_n - a_m$$$ separately. This leads to a simple $$$n^2$$$ solution: 90999997.
Note that by using RMQ we can improve this to $$$\mathcal{O}(n \log n)$$$ or even $$$\mathcal{O}(n)$$$. The idea is very similar to the solution to problem G here.
1400F - x-prime Substrings
The key observation is that since $$$x$$$ is only up to 20, there can't be that many different $$$x$$$-prime strings total--turns out there are only about 2400 for the worst case of $$$x = 19$$$. So we can generate all of them and perform a DP where our state is represented by the longest prefix of any of the strings we currently match. We can do this by building a trie of all of the $$$x$$$-prime strings. We then need to be able to transition around in this trie; it turns out this is exactly what Aho-Corasick does for us. In particular, knowing which node of the Aho-Corasick tree we are currently at gives us the full information we need to determine whether or not we will match one of the strings after adding more characters later. This leads to a fairly simple DP: 90977148
1400G - Mercenaries
In order to take care of the $$$l_i$$$ and $$$r_i$$$ constraints, we can iterate on the number of mercenaries we'll choose and find the number of choices for each count. The key constraint in this problem is that $$$m$$$ is at most 20, which means that there can only be a few connected components that aren't just a single node. In particular, the largest possible connected component size is 21 (since a connected graph with $$$m$$$ edges has at most $$$m + 1$$$ nodes).
This means that for each connected component we can iterate over all of the subsets of nodes in that component and check whether the subset is a valid choice (i.e., is an independent set). We can then do a DP for each component where dp(mask, k) = the number of submasks of mask that have k ones and represent a valid independent set subset of the component.
Finally we can iterate over the total number of mercenaries we want. We can then do a knapsack over each of the components, making sure to only consider nodes in each component where $$$l_i$$$ and $$$r_i$$$ work with our number of mercenaries. Finally we determine how many valid $$$l_i, r_i$$$ mercenaries are available outside of our components, and the rest is a simple choose function. Code: 90977154
Today for problem 1391E - Pairs of Pairs I didn't come up with the clever DFS tree solution, but I found an interesting constructive algorithm instead:
The main idea is to build a path and a pairing at the same time. We will eventually include every node in either the path or the pairing, at which point we're done.
We keep a set of unused nodes, and we repeatedly try to extend the end of our path by adding one of these unused nodes to the end. We can keep making progress until the end node of our path u only has neighbors that are either already in our path or already in our pairing. When this occurs, we take u and pair it with any unused node v, and then we add this pair to our pairing.
What if this makes the pairing invalid? In that case, since none of our pairs have an edge directly in between them, there must be two other nodes a and b such that at least 3 of these 4 edges exist: u-a, u-b, v-a, v-b. In particular, this means either u-a-v or u-b-v exists as a path, so we can remove the a, b pair and use this to extend our path instead. We can show that this process will monotonically make progress toward our goal state of having every node in either the path or the pairing. But how do we check efficiently whether the pairing becomes invalid? Instead of iterating over every pair, we can iterate over the neighbors of u and check only the pairs containing any of those neighbors.
The potential issue here is that we could iterate over the neighbors of the same node many times, if we repeatedly get it at the end of our path. So it may be possible to TLE the solution. Can anyone find a case to hack this? Here's the link: 89441355
Let's look at two problems from the last round, Round 657 (Div. 2):
Problem D 1379D - New Passenger Trams currently has 367 solvers and had 77 solvers in the official contest (among rated participants).
Problem E 1379E - Inverse Genealogy currently has 44 solvers and had 0 solvers in the official contest.
Meanwhile both problems have the same difficulty rating of 2400. How does that make any sense?
I believe I have an $$$O(n \log n)$$$ solution to 1312E - Array Shrinking. Here's the code: 72938462
The main idea is to find all segments of the array that can be reduced to a single number. We do that via this DP:
reduce(start, x) = the end of the range starting at start that can be reduced to the single value x, or -1 if no such range exists. You can then solve this DP with the recurrence reduce(start, x + 1) = reduce(reduce(start, x), x).
The key claim is that there can be at most $$$n \log n$$$ such segments, no matter what the $$$a_i$$$ are. In fact, the maximum possible number of such segments seems to be exactly the number of segments when all of the $$$a_i$$$ are equal. This version of the code adds an assertion to test this claim: 72938781. It passes every small random test case I've given it.
Unfortunately I don't have a proof of this claim yet, but it feels like there should be a nice proof. Can anyone come up with something? One approach could be to prove a slightly stronger claim, that there are at most $$$n \log n$$$ segments where $$$\displaystyle \sum{2^{a_i}}$$$ is a power of two.
Given the numbers $$$1, 2, \dots, 20$$$, you want to choose some subset of these numbers such that no number you choose is divisible by any other number you choose. What's the largest subset you can get?
One simple idea is to choose all the primes: 2, 3, 5, 7, 11, 13, 17, and 19, leading to a subset of size 8. But you can do better! Try to figure out the solution yourself before reading below.
For 1292F - Nora's Toy Boxes from Round 614 Div. 1, after you make several observations and pull out a sick counting DP, you get a solution that is $$$\displaystyle \mathcal{O} \left (N^2 \cdot 2^S \right )$$$, where $$$S$$$ is the number of values in our array $$$A$$$ that are 1) not divisible by any other value in $$$A$$$ and 2) have at least two other values in $$$A$$$ divisible by it. (These are the only values we should consider using as $$$a_i$$$ in the operation described in the problem.) So what is that time complexity really?
Don't worry if you haven't actually read or tried to solve the problem. In the rest of this post I'll focus on this question: out of all subsets of $$$1, 2, \dots, N$$$, what is the maximum possible value of $$$S$$$? I'll show that we can attain a precise bound of $$$\displaystyle \frac{N}{6}$$$.
Let's call the numbers that satisfy our constraints above special. First, since each of our special numbers needs to have two other multiples in $$$A$$$, any special number $$$x$$$ must satisfy $$$3x \leq N$$$, so $$$\displaystyle x \leq \left \lfloor \frac{N}{3} \right \rfloor$$$. So we should just find the maximum subset of $$$\displaystyle 1, 2, \dots, \left \lfloor \frac{N}{3} \right \rfloor$$$ such that no number in our subset divides another, and then we can add every number greater than $$$\displaystyle \left \lfloor \frac{N}{3} \right \rfloor$$$ to ensure that we hit the second requirement of at least two multiples for each.
With $$$N = 60$$$ in our case, this leads to the problem described above: given the numbers $$$1, 2, \dots, 20$$$, what is the largest subset of these numbers we can choose such that no number we choose is divisible by another number we choose? The answer turns out to be 10. First we provide a simple construction: choose $$$11, 12, \dots, 20$$$. (We can also generalize this: for $$$1, 2, \dots, K$$$ the answer is $$$\displaystyle \left \lceil \frac{K}{2} \right \rceil$$$.)
Now we need to prove that this is the maximum possible. We can do this by building the following chains of numbers:
- 1 — 2 — 4 — 8 — 16
- 3 — 6 — 12
- 5 — 10 — 20
- 7 — 14
- 9 — 18
- 11
- 13
- 15
- 17
- 19
Every number occurs in exactly one chain, and we can never take two numbers from the same chain. So our subset can't be larger than the number of chains, which is again exactly 10. (In general it's the number of odd numbers up to $$$K$$$, which is again $$$\displaystyle \left \lceil \frac{K}{2} \right \rceil$$$.)
So in the general case, the maximum value of $$$S$$$ is exactly $$$\displaystyle \left \lceil \frac{\left \lfloor \frac{N}{3} \right \rfloor}{2} \right \rceil = \left \lfloor \frac{N + 3}{6} \right \rfloor$$$, meaning the algorithm has a complexity of $$$\displaystyle \mathcal{O} \left (N^2 \cdot 2^{\frac{N}{6}} \right )$$$.
Thanks scott_wu for discussing and thinking through this problem.
saketh and I were looking at 1272F - Two Bracket Sequences and challenged ourselves to solve it using as little memory as possible. From my initial submission using 118 MB, I was able to get down to 19 MB using int16_t for DP values and using single bits for the previous step markers: 66735626.
Saketh then got it down to 3.2 MB by solving the DP using BFS to remove the DP array entirely: 66740348 (according to him, the DP values are implicit in the BFS).
Finally, we came up with a new idea to both eliminate the previous step markers and store the DP values efficiently using the observation that each DP value is +1 or -1 compared to the previous value. This uses 1.4 MB: 66796767. It's actually still $$$n^3$$$ memory, but it uses only 1 bit per entry.
Can anyone do better than this? Perhaps someone can even come up with an approach using sub-$$$n^3$$$ memory.
Inspired by the discussion at Almost-LCA in Tree, I wanted to pose a similar question:
Is there a simple solution to
- preprocess a tree with weighted edges in $$$O(n)$$$ or $$$O(n \log n)$$$ and
- query the maximum edge weight along the path from $$$u$$$ to $$$v$$$ in O(1)?
Once again, jump pointers can be used to solve each query in $$$O(\log n)$$$ with bad constant factor. Are there faster solutions?
Since there was a fair amount of interest, I'll explain here how I optimized my solution to 1249F - Maximum Weight Subset from $$$\mathcal{O}(n^4)$$$ to $$$\mathcal{O}(n)$$$. One cool feature of this problem is that it's possible to get from $$$\mathcal{O}(n^4)$$$ all the way down to $$$\mathcal{O}(n)$$$ with fundamentally the same solution idea. This is unlike many other problems, where if you want to improve the runtime further you have to completely rethink the solution from scratch (e.g., switch to greedy rather than DP). Thanks MikeMirzayanov for writing a nice problem.
$$$\mathcal{O}(n^4)$$$
I'll briefly go over the inefficient solutions first. My initial idea was to compute for each node a two-dimensional DP: dp[n][d] = the maximum weight to choose n nodes in a valid manner within our subtree such that the node closest to the root of the subtree has depth d. Then when combining two subtrees, we need to add the node counts together and take the minimum of the two depths to get our new DP state. Code here: 63153425. Pay attention to the attach function in particular.
This looks like $$$\mathcal{O}(n^5)$$$, but it's actually $$$\mathcal{O}(n^4)$$$ due to this observation. I wasn't sure at first if this would manage to pass the time limit, but it turns out the worst case is only around $$$100^4$$$ with good constant factor, rather than $$$200^4$$$.
$$$\mathcal{O}(n^3)$$$
To optimize the above solution, notice that the nested inner loops on x and y can be optimized to linear time by computing suffix minimums of the original DP arrays. We consider two cases for min(x, y), one where x = min(x, y) (in which case we need both y >= x and x + y >= K, meaning y >= max(K - x, x)) and another case where y = min(x, y) (with similar constraints on x). Code: 63200545. Note that the innermost loops perform the equivalent of the commented-out loops on x and y, with complexity improved by a factor of $$$n$$$.
A better $$$\mathcal{O}(n^3)$$$
How can we do better? Well, it would be helpful if we realized that the n for node count in our DP state is completely useless. Let's get rid of it. Now our solution looks like this instead: 63200548. A much cleaner $$$\mathcal{O}(n^3)$$$.
[Correction: this is actually $$$\mathcal{O}(n^2)$$$ due to the same observation as above.]
$$$\mathcal{O}(n^2)$$$
Here we apply the same suffix max optimization again. Code: 63200549. We've now reached the best solution described in the editorial.
$$$\mathcal{O}(n \log n)$$$
How can we improve further? Let's take a look at the quadratic solution again and analyze which parts are causing it to be quadratic. First the algorithm requires inserting into the beginning of a vector; this is easy to fix by swapping out std::vector for a std::deque and using push_front(). On top of that, the inner loops to combine two subtrees clearly cause the algorithm to be quadratic.
However, note that we can rewrite the attach function to run in time proportional to min(root.size(), child.size()) rather than root.size() + child.size(). In particular, the code to combine the two subtrees is completely symmetric with respect to root and child, so we can swap if necessary in order to assume root.size() >= child.size(). We can then combine the two subtrees in O(child.size()) by
- saving the suffix maxes in the DP state so we don't have to recompute them and
- realizing that we can limit the loops on both
xandyto go up tochild.size()only, since any indices larger than that will not get modified for our combined DP state.
Thus, after being careful to pass everything by reference to avoid redundant copying, our new algorithm is $$$\mathcal{O}(n \log n)$$$, since every DP state can only be merged from smaller into larger $$$\log n$$$ times each. Code: 63206899. For an easier implementation, note that we can just use the suffix maxes as the DP state itself; in other words, we redefine the DP state to be dp[d] = the maximum weight we can get from validly choosing nodes in our subtree such that all chosen nodes are *at least* depth d from the subtree root.
$$$\mathcal{O}(n)$$$
But our time bound on our algorithm can be improved -- it's actually $$$\mathcal{O}(n)$$$. How come? This is due to the fact that instead of having one DP state per node in our subtree, we have one DP state per distinct depth in our subtree. In particular, this means that merging a smaller state into a larger state results in an output of the same size as the larger state, rather than the sum of the two sizes (like in the usual smaller-to-larger case). So when we merge smaller into larger, you can think of it instead as all of the smaller state values getting 'eaten' by the larger state, in O(1) time per value. Since each value can only get eaten once, we can finally conclude that our algorithm is $$$\mathcal{O}(n)$$$.
When trying to generate some of my own test cases for 1190E - Tokitsukaze and Explosion, I noticed that it was hard to make cases where even slightly large values of $$$m$$$ didn't all give the same answer. After some thinking this makes perfect sense, because with larger values of $$$m$$$, points that are very far away from the origin become almost freebies; only the few closest points to the origin should really matter.
So on a whim, I tried submitting some 'incorrect' code to the problem. After several rounds of experimentation (in other words, even more binary search), I found that you can add this line to your code:
M = min(M, 4);
and still get accepted. Turns out you don't need all the $$$2^k$$$ jump pointers which were mentioned in the editorial; you can just iterate each element four times instead. ;)
I'll try to generate some stronger test cases. Should be a good chance to try out the new uphacking feature.
EDIT: I generated three strong cases with M = 18, M = 200, and M = 1025 ("strong" meaning that increasing M further still changes the answer). They're now all in the system tests. You'll notice them if you get WA on test 149 or later.
Did anyone else notice this issue come up today? When trying to hack in my room (via Chrome on Linux), I got a message saying that I needed to update Flash in order to continue. I clicked the update button, which refreshed the page and showed me the code in an almost unreadable font: non-monospaced, letters were all squished together, and l looked exactly like 1.
I just tried installing more fonts which I think might fix it. Does anyone know a way I can check on my hacking font again? Now that the contest is over, when I open code in my room it just shows the normal copy-pasteable code window instead.
Continuing with the theme from last time, here's a quick writeup of my approaches:
1107A - Digits Sequence Dividing
Since we just want to make two numbers such that the first number is smaller than the second, our best bet is to use only the first digit for the first number and the rest of the digits for the second number. Note that since the numbers can have up to 300 digits we shouldn't actually evaluate the second number. Instead, since the digits only include 1 through 9, we can handle that case by checking the number of digits. Code: 49002957
1107B - Digital root
The key observation is that the digital root of an integer k is the single-digit number 1 ≤ d ≤ 9 such that 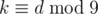 . You can prove this by noticing that
. You can prove this by noticing that 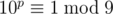 for all p. Once we observe this, finding the k-th number is very simple; see the code: 48993705
for all p. Once we observe this, finding the k-th number is very simple; see the code: 48993705
1107C - Brutality
Since we are only allowed to push the same button k times in a row, let's do a two-pointer sweep to find all segments of consisting of just one button. Within each segment, we'll sort and take the k highest values. See the code for details on the two-pointer sweep: 48994498
1107D - Compression
After some tinkering with the given condition, we notice that an x-compression is possible iff x divides n and the n × n matrix is divisible into x × x matrices such that each matrix is either all 1 or all 0. We can loop over all such x and check the condition in n2 time per x, but this is potentially too slow.
To speed this up, we can precompute rectangle sums for every rectangle containing the upper-left corner, which enables us to compute the sum of any rectangle in 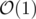 . This improves our time complexity to
. This improves our time complexity to 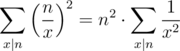 . Since
. Since  (really!), this means our solution is
(really!), this means our solution is 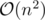 . Code: 49028814
. Code: 49028814
1107E - Vasya and Binary String
We set up a DP on (start index, end index, number of consecutive digits matching our start index). In other words, the current string we are solving is the substring from start index to end index, plus some number of additional digits (all equal to S[start]) added as a prefix to our substring.
We then have two choices from any given state:
- Cash in on our consecutive digits at the start and recurse on
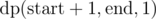 .
. - Pick an index i such that S[start] = S[i], and collapse everything between those two indices in order to merge them together for an even larger prefix. This results in a score of
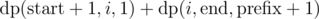 , and we can loop over all i to take the maximum.
, and we can loop over all i to take the maximum.
The runtime is 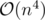 , with a very good constant factor. Code: 49036191
, with a very good constant factor. Code: 49036191
Does anybody have 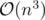 ?
?
1107F - Vasya and Endless Credits
Notice that if we take offer i exactly m months before we buy the car, it will provide us with 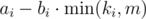 money at the time of the car purchase. Moreover, the only values of m that make sense are 0 ≤ m ≤ n - 1. This means we can immediately solve the problem via an algorithm for the assignment problem, such as min-cost flow or the Hungarian algorithm. This has a runtime of
money at the time of the car purchase. Moreover, the only values of m that make sense are 0 ≤ m ≤ n - 1. This means we can immediately solve the problem via an algorithm for the assignment problem, such as min-cost flow or the Hungarian algorithm. This has a runtime of 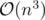 or
or 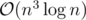 , which manages to fit under the time limit with a good implementation. Code: 49033783
, which manages to fit under the time limit with a good implementation. Code: 49033783
The better solution is to notice that for all offers i where we don't use up all ki months, it's best to sort them by bi (so that the highest values of bi have the lowest values of m). This leads to a very nice 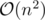 DP solution: 49035446
DP solution: 49035446
1107G - Vasya and Maximum Profit
We can first compute all values of 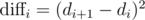 . Since we only care about the maximum such value within our segment, we can use div-conquer to solve every segment. In particular, if we know the index of the maximum value in
. Since we only care about the maximum such value within our segment, we can use div-conquer to solve every segment. In particular, if we know the index of the maximum value in 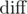 , we know that any segment crossing this index has this value as its maximum. We can thus solve all segments crossing this maximum and recurse on the left and right sides.
, we know that any segment crossing this index has this value as its maximum. We can thus solve all segments crossing this maximum and recurse on the left and right sides.
To find the best crossing segment, note that each problem contributes a value of a - ci. We can independently find the largest sum starting from our crossing index going left and the largest sum going right, and add these two together for the best overall crossing segment.
Unfortunately, since we can't guarantee that the maximum indices will divide our interval nicely in half, this does not lead to the usual 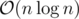 runtime of div-conquer but is instead
runtime of div-conquer but is instead 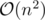 in the worst case. To improve on this, we can precompute partial sums of a - ci and use RMQ to find the minimum sum left of the crossing index and the maximum sum right of the crossing index. This reduces the crossing computation from
in the worst case. To improve on this, we can precompute partial sums of a - ci and use RMQ to find the minimum sum left of the crossing index and the maximum sum right of the crossing index. This reduces the crossing computation from  per index to
per index to  or
or 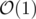 , giving an overall runtime of
, giving an overall runtime of 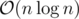 . Code: 49036431
. Code: 49036431
Just finished this contest in virtual mode and noticed the editorial is missing, so I thought I would share my approaches.
1100A - Roman and Browser
Loop over all values of b and take the sum of all indices that are not equivalent to 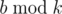 . Remember to take the absolute value at the end. Runtime is
. Remember to take the absolute value at the end. Runtime is 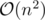 . Code: 48374675
. Code: 48374675
1100B - Build a Contest
Maintain a frequency array of size n and track the number of distinct values seen so far as we loop through the array. Once the number of distinct values reaches n, we hold a round and decrement each index of the frequency array. Note that this takes n time, but this is fine since we can only hold at most  rounds. Runtime is
rounds. Runtime is  . Code: 48374608. Note that
. Code: 48374608. Note that x++ means use the value of x and then increment, whereas ++x means increment and then use. Similar for x-- and --x.
1100C - NN and the Optical Illusion
Draw the line segments between the center of the inner circle and the centers of two adjacent outer circles. These three line segments form a triangle. If the inner radius is r and the outer radius is R, then the sides of the triangle are r + R, r + R, and 2R. We also know that the angle of the triangle at the center of the inner circle is 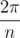 . Now we can apply the Law of Cosines and some algebra to solve for R. Code: 48374823
. Now we can apply the Law of Cosines and some algebra to solve for R. Code: 48374823
Update: for an even easier method, we can realize that we can cut the angle above in half, which results in 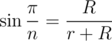 .
.
1100D - Dasha and Chess
This problem has a very clean mathematical solution. It turns out 666 rooks is just enough for us to solve the problem.
First, move to the center of the board, (500, 500). We can do this using at most 499 moves. If any rook is on our row or column we're done, so we can assume that's not the case. Then every rook is in one of the four quadrants surrounding us. Notice that by moving diagonally 499 times in a row, we can fully 'sweep' any of the quadrants we choose.
In addition, every rook is accessible by either row or column in exactly three of the four quadrants. Since 3 × 666 = 1998 > 4 × 499, there must be some quadrant where at least 500 rooks are accessible. We can simply sweep this quadrant fully in 499 moves, and there is no way for our opponent to remove all the rooks fast enough. Code: 48378396.
Make sure to handle this case correctly to avoid Wrong Answer: "The king cannot move onto the square already occupied by a rook." (In this case we should easily be able to find a move that immediately wins.)
1100E - Andrew and Taxi
First, struggle to solve the problem for a while. Then realize that you didn't pay enough attention to this sentence: "It is allowed to change the directions of roads one by one, meaning that each traffic controller can participate in reversing two or more roads." So in particular, we are not looking for the sum of modified edges' weights but instead the maximum edge weight we need to modify in order to remove all cycles from the graph.
When we want optimize the maximum of a set of things, it's a good idea to binary search. Let's say we are binary searching and we have a number C. Then we want to know if it's possible to remove all cycles by only allowing ourselves to reverse edges with c ≤ C.
This turns out to have an efficient solution. First, consider all of the edges with c > C. These edges must not contain a cycle, or else we can immediately decide that C is not good enough. If they don't contain a cycle then they will form a directed acyclic graph (or DAG), and we can perform a topological sort of this graph. Then for every remaining edge (c ≤ C), since we have the option to reverse it if we like, we can choose to point the edge in the same direction as the topological sort. Since all edges are then ordered according to the topological sort, there cannot be any cycles. Runtime is 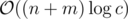 , which can be improved to
, which can be improved to 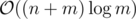 if desired by binary searching on the sorted list of edge weights instead. Code: 48376981
if desired by binary searching on the sorted list of edge weights instead. Code: 48376981
1100F - Ivan and Burgers
Except for the very weird cover story, this problem is similar to 1101G - (Zero XOR Subset)-less (but harder). I recommend solving that problem first before attempting this one. Both problems are made easier with some knowledge of linear algebra.
For this problem, we want to find the maximum number attainable via XOR within subarrays of our given array. The best way to do this is to treat the numbers as vectors in  and compute a basis (https://en.wikipedia.org/wiki/Basis_(linear_algebra)) of the vector space. In other words, we want to find a minimal set of numbers that we can combine together to generate the full vector space. Since the numbers only have
and compute a basis (https://en.wikipedia.org/wiki/Basis_(linear_algebra)) of the vector space. In other words, we want to find a minimal set of numbers that we can combine together to generate the full vector space. Since the numbers only have  bits, one can prove that the basis will have a size of at most 20.
bits, one can prove that the basis will have a size of at most 20.
My approach was then to create a seg tree on the array where each node stores a basis of its subarray. Note that it helps to store the basis in strictly decreasing order of highest bit. I join two bases in 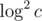 time, for an overall runtime of
time, for an overall runtime of 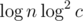 per query, which barely fits in the time limit at 2.6s. Code for reference: 48396593. Watch out that ci = 0 is allowed!
per query, which barely fits in the time limit at 2.6s. Code for reference: 48396593. Watch out that ci = 0 is allowed!
It is also possible to solve the problem in  or even
or even 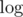 time per query. One key idea is to compute for each L the at most 20 different R values that increase the size of the basis for the subarray from L to R. See the comment section below for discussion.
time per query. One key idea is to compute for each L the at most 20 different R values that increase the size of the basis for the subarray from L to R. See the comment section below for discussion.
1043D - Mysterious Crime requires you to input 1 million integers and ultimately process them in either nm or 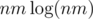 time. But the time limit was set to only 1 second. This is very unfriendly to any language that isn't C++, and it even puts
time. But the time limit was set to only 1 second. This is very unfriendly to any language that isn't C++, and it even puts 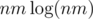 C++ solutions at risk of failing.
C++ solutions at risk of failing.
Case in point: tourist's contest submission uses an STL map and exceeded the time limit, causing him to drop over 100 places. Meanwhile, ksun48 and mnbvmar had almost exactly the same solution and barely squeezed by the time limit in 998 ms. tourist was also able to pass with the same code in practice mode by switching from C++11 to C++14, which shows how close it was.
I admit there are certain problems where it is interesting to distinguish O(n) and  solutions, but this doesn't fit that case, as it doesn't take any novel insight to remove the log from the runtime here. Overall it would have been much better with a time limit of 2 or 3 seconds; or alternatively, with m ≤ 5 instead of 10.
solutions, but this doesn't fit that case, as it doesn't take any novel insight to remove the log from the runtime here. Overall it would have been much better with a time limit of 2 or 3 seconds; or alternatively, with m ≤ 5 instead of 10.
For today's Div 1 problem D, 1067D - Computer Game, once you succeed at a quest, it's clear you should upgrade and play the quest that maximizes your expected reward pi × bi for the remainder of the game.
However, before you succeed at a quest, you have a difficult tradeoff to make: should you take a quest with a high probability of succeeding, to maximize your chances of upgrading and gaining optimal points for the rest of the game? Or should you take a quest that gives you more expected reward pi × ai right now?
It turns out the answer to this tradeoff depends on T, the number of seconds left. As T gets smaller, we should switch to quests with lower pi but higher immediate reward pi × ai. This is because the long-term value of upgrading and maximizing future rewards becomes less relevant compared to getting more reward now. In particular, the optimal quest to pick (when we have not yet succeeded at any) can change multiple times as T gets smaller and smaller. My solution 44819755 uses multiple binary searches along with a stack to determine the optimal switching points.
Unfortunately, the system tests are extremely weak at testing this logic. Many competitors submitted solutions that never even choose to switch quests. This actually passes all of test cases 1 through 104. It will only fail on test case 105, the very last test case, where ironically N = 2:
2 10
1000 1001 0.1
10 1000 0.5
In this case, except when T = 1 you should always perform the second quest, as this gives you a 50% chance of upgrading and getting 0.5 × 1000 = 500 expected reward every turn thereafter. However, when T = 1, upgrading has no more value, so you should perform the first quest instead for an expected reward of 0.1 × 1000 = 100, as opposed to the second which only gives 0.5 × 10 = 5 immediate reward. So this test case requires just one quest switch at the very end.
This case was enough to catch the majority of wrong submissions. However, since it's very simple, it was still possible for incorrect solutions to get through. In-contest, I believe only one did: 44804123. In particular here is a case where two switches are required:
3 3
3 4 0.5
6 25 0.4
15 16 0.2
The maximum pi × bi here is 0.4 × 25 = 10, which is the amount we will get each turn after succeeding and upgrading.
When T = 1, we should choose quest 3 for an immediate reward of 0.2 × 15 = 3, the maximum possible.
However when T = 2, we should choose quest 2, which gives us an expected value of 0.4 × (6 + 10) + 0.6 × 3 = 8.2. Choosing quest 3 only gives us 0.2 × (15 + 10) + 0.8 × 3 = 7.4. Similarly, choosing quest 1 only gives us 8 points.
When T = 3, we should actually choose quest 1, which gives us an EV of 0.5 × (3 + 2·10) + 0.5 × 8.2 = 15.6. This is higher than choosing quest 2, which gives us 0.4 × (6 + 2·10) + 0.6 × 8.2 = 15.32.
So the answer for this test case is 15.6. However bazsi700's Accepted solution above outputs 15.5 because it never uses quest 2.
If you're working on this problem in practice mode and want to know whether you actually solved it, make sure to test the case above and a few others like it!
C++ has always had the convenient data structures std::set and std::map, which are tree data structures whose operations take  time. With C++11, we finally received a hash set and hash map in
time. With C++11, we finally received a hash set and hash map in std::unordered_set and std::unordered_map. Unfortunately, I've seen a lot of people on Codeforces get hacked or fail system tests when using these. In this post I'll explain how it's possible to break these data structures and what you can do in order to continue using your favorite hash maps without worrying about being hacked
| Name |
|---|