Tutorial is loading...
Tutorial is loading...
Author's solution Tutorial is loading...
Author's solution Tutorial is loading...
Author's solution Solution of bonus task Tutorial is loading...
Author's solution Tutorial is loading...
Author's solution Tutorial is loading...
Author's solution Tutorial is loading...
Author's solution









Auto comment: topic has been updated by aleex (previous revision, new revision, compare).
For Div C ,i know that a[l]^a[l+1]........a[r]=0 . But how can we say that for every subarray of even length such that its xor sum=0 ,then xor of its first half is also equal to xor of second half.
Correct me if i am getting it wrong but can't there be any subarray whose xor sum is 0 but xor of first half != xor of second half.
There can't be any such subarray.
Let's say the xor sum of left half is x. So the xor value for right half will be 0^x = x
Yeah ,that was a silly question.
Let's focus on an 0/1 sequence, such as 0 0 0 1 1 0 1 1. Now, We have a[l]^a[l+1]........a[r]=0, that means the number of "1" in this sequence is even. We have the conclusion that even number of "1"'s xor is 0, and odd number of "1"'s xor is 1, so xor(l->mid) != xor(mid+1->r) means one part's count of "1" is odd, and the other's is even, which contradicts with the assumption. Sorry for my poor English :(
xor of right half is also 1 as the number of 1's odd's.
I got the same doubt during contest and couldn't figure out. :(
thanks for fast editorial!
Very interesting to know how many people got AC on Div.1 D without using google :)
Very interesting to know how many people you need to come up with such an interesting problem as D.
Was there a direct formula available online?
Yes!!! https://www.turgor.ru/lktg/2018/3/3-1ru-sol.pdf
3.4?
I didn't use Google, just thought that the formula looks something close to the Cayley's formula nn - 2 (appeared to be a little harder), drew some small cases and noticed the pattern.
Yes, but I think that you spend much time to find this formula without Google and people who used google had really more time to other tasks
Instant editorial
Here is the proof of the generalized Cayley's formula (link from Wikipedia sources).
I failed to work this out myself and lost an hour :(. Next time I'll try Google first.
Great contest, but It would have been better if the setter had allowed only O(n) to get accepted in DIV 2D.
I dont think it would really change anything since you can solve this task with hashes in linear time too, without any advancement in idea of solution. I reckon most of people would use it instead of risking and spending more time on thinking.
Well, I don't agree because if you see the submissions, almost everyone has used brtue force O(n^2) solution. Do you really think that Div. 2D should be all about implementation and brute forcing and checking every possible scenario ? Because of you solved in linear time doesn't mean everybody would have solved in linear time too.
UPD: Even he/she has used O(n^2) solution. LOL
You didn't understand me. I meant that O(n^2) can easily become O(n) if you use hashes. D div2 does not usually require knowledge of any algorithms at all, except the most primitive ones. But in the way you suggest, people who know algorithms would have an advantage over people who don't, which is not right if we are talking about D div2.
Sorry, but again I can't agree. It's solving Div. 2D that seperates a Div2 candidate from a Div1 candidate. Your line: "people who know algorithms would have an advantage over people which is not right", well this statement is incorrect for any problem.
Also, FYI in this question we are not using any algo to get O(n), It's simple string comparison.
You can do Div2D in O(N) without hashes, by using an ad hoc proof. See my other comment below.
In A Div2 If v=n-1 Isn't the answer equal to n-1?
For E, I think the maximum number of primes is 9 instead of 8 since 3 is also a prime
Really, I calculated it, but missed in editorial. Thanks
Can anyone explain what "So to count the answer just have two arrays cnt[0][x] to store elements from even positions and cnt[1][x] for odd positions. Then iterate i from 1 to n and add to the answer cnt[imod2][prefi]. After you processed i, increase cnt[imod2][prefi] by 1" mean in Editorial of Problem 1109A
Just try to read accepted solutions, should be helpful.
Thanks...will try..!
but can you please give some hint why are we doing it , and what does it do ?
Here are couple of hints: 1. Store even and odd positions separately because this is required for r — l + 1 to be of even length. A pair is found when a segment l....r is found whose xor is zero.
Why cnt[1][0] start from 1 not 0 ?
For a particular case when xor of whole array will be 0. Then we need cnt[1][0]=1 to get the answer=1.
Author's solution should be included too.
I solved 1109D - Sasha and Interesting Fact from Graph Theory without using the generalization of Cayley's formula — because I didn't know that generalization.
I tried to get O(n2) solution first. I iterated over the distance between a and b (just like the editorial describes) and then over the degree of the fake vertex (i.e. total degree of the path between a and b). Prufer codes give us a way to compute the number of trees where one vertex has some given degree: it means that this number must occur exactly deg - 1 times in the sequence of size n - 2, so the formula is for a tree with n vertices. We multiply that by some other stuff like (edges - 1)! for rearranging vertices on the path etc. This way we get O(n2) solution and to make it faster we need to compute the following sum fast for two constants C and D (I got something similar after simplifying formulas):
for a tree with n vertices. We multiply that by some other stuff like (edges - 1)! for rearranging vertices on the path etc. This way we get O(n2) solution and to make it faster we need to compute the following sum fast for two constants C and D (I got something similar after simplifying formulas):
It's easy to make a story for that to get a formula: we want to choose i of C soldiers, and then choose one of D colors for every chosen soldier. Instead, we can say that every soldier gets one of D + 1 types and the last type D + 1 means that this soldier is not chosen at all. So the sum is equal to:
I think that Prufer codes isn't a popular thing
Every tree corresponds to a sequence of length n - 2 where the degree of vertex a is equal to the number of occurrences of a in the sequence minus 1. Here you go, now you know it.
This is enough to solve div1D today and it's enough to get formula nn - 2 for the number of trees with n vertices. But there are some more facts about Prufer codes — read Wikipedia for that.
Thank you! Now I really know it, but now I know the generalized Cayley's formula too! The problem is that the most part of people (and me too) didn't know it before the contest!
Thank you very much for your nice solution! I also tried to solve the problem with the help of Prufer Code, but I didn't realize that I could enumerate the degree to get the O(n^2) solution... btw, the last step in your solution can be immediately shown from the binomial theorem.
For div.2 problem B please anyone explain following test case n=8 1 1 1 1 1 1 100 100
my question is how output is comes 125 please help anyone
1*10+1+1+1+1+1+100//10+100=125
thanks a lot for a quick response. i made mistake to read the question. " 2D can at most once choose an arbitrary integer x ". This Line.
same bro
In Div1D, when we fix edges, why are we taking combinations of edges-1 vertices and not permuations ?
I have TL with this code!
https://pastebin.com/ds9FkhiC
Do you know why?
After the competitetion I solve the same code and now I have AC https://codeforces.com/contest/1109/submission/50036496 https://codeforces.com/contest/1109/submission/50005524
You didn't use your fastio()
But why the same code have AC after round?
Your AC solution was close to TL.
There's always some variance between different runs of the same code, so it is possible to TLE on an unlucky run.
May be, but in AC variant time less than 0.960 s, it's rather strange
Auto comment: topic has been updated by aleex (previous revision, new revision, compare).
I did the Div2 B question using STL map in C++ , but got a runtime error in the last system test . I was erasing the keys having 0 value . I resubmitted it after removing the part where I am erasing from the STL map and it got accepted . This has happened before also when I was trying to erase from a STL set. Can anyone elaborate why runtime error occurs in such cases !!
Submission with runtime error : 50026129
Submission with AC : 50037712
Why don't you just copy failed test and try to debug your program locally?
3 1 36 38
Hf with that.
I did that my compiler is showing the correct answer without any runtime error !!
It's not correct to erase from map or set the way you do, while you iterating over it. Because the sequence of elements changes and further iterators changes too,i guess. Erase function returns correct iterator on the next element (you can read about return value there http://www.cplusplus.com/reference/set/set/erase/), so you should check first, is there such element to erase? if yes than it=Seta.erase(element), else ++it. Something like that. Hope i helped you.
50009667
O(n) solution for div1B without string algorithms. (Ignore everything before function go(l, r))
Nevermind, didn't notice author's solution for bonus problem.
Do you have any proof for your solution?
No, I don't. During the contest it just seemed to be the right solution, because I didn't notice the constraints on length of the string (I was solving for 105)
Div 1B: Bonus task is to solve this in linear time, but does not author's solution work in worst case O(n log n)?
No. The recursion has cost T(N) = O(N) + T(N / 2). This is O(N). Think of it as N + N / 2 + N / 4 + N / 8 + .... this is <= 2 * N
Worth remembering, thank you.
What's the proof that ans of div2D can be atmost 2 ?
Assuming your are in the case where there is an answer find the smallest i such that s[0] ≠ s[i] then cut off the substring from 0 to i and the corresponding part on the right. Swap these two pieces and you get a different palindrome as required. It is different because the first character is s[i] and it is a palindrome because the two parts cut off are the reverse of each other since s is a palindrome.
Thanks for the explanation. I just forgot that answer asked for minimum cut.
Think of it as s="aaaab anythinggnihtyna baaaa". You can always make 3 pieces in the following manner. s1="aaaab", s2=" anythinggnihtyna ", s3="baaaa". Swap s1 and s3 and you got yourself a new palindrome. Now, imagine the case where this s2 is empty string. Then it becomes actually 2 pieces only, so k=1 is the answer. Be extra careful to check whether this makes the new string same as the old one.
with "aaaab anythinggnihtyna baaaa" as string , I think we can split this just 2 pieces. str1 = aaaab anything str2 = gnihtyna baaaa
new string = gnihtyna baaaa aaaab anything.
That's exactly what I said (wanted to say, to be precise). Maybe I couldn't make it clear enough.
I said that you can always make 3 pieces in this manner, taking the first substring containing all same letters followed by the first different letter and its corresponding reverse string from the end of the string. What I actually meant here is that 3 pieces is the maximum you will need, ever, if the answer exists.
But you can make the s2 empty if you don't stop yourself at the first different letter and go upto the middle point, like you said in the example I used above.
And obviously this can't be done always if the substring upto the midpoint is actually repeated twice in the original string, such as ".aabbaa..aabbaa.", where this midpoint breaking will fail as this will return the same string as the initial one. However, you need to recursively check for such a midpoint breaking technique in the newly found 'half string', the string ".aabbaa." in this case. Here, the string ".aab" and "baa." are not the same, so you can start build the original new palindrome "baa..aabbaa..aab" starting from the later part, or 4th index of the string.
I hope this make it clear.
I wonder how we can solve Problem C from Div.1 using segment tree in O(log(q)) per query. I came up with nearly the same solution, but what I have in mind for the type-3 query is to binary search the earliest time that the time get under 0, which will cost O(log(n)2). Can someone tell me if there is a better way to do this?
You can do binary search on a tree in O(log). Start from a leaf that represents the start of interval L, then go up for some time, merging with right children all the time. Eventually we will get a merged interval that already contains the answer, so we start going down.
Oh, I get it. Essentially, the query interval will be split into O(log(n)) continuous intervals, and I can start merging from the leftmost interval to see whether the minimum is below zero. If mim becomes under zero upon merging a node, I can start descending from the current node to perform some binary-searchish thing.
Thank you for your explanation!
For 1113A — Sasha and His Trip
We can also solve it in less complexity O(1) without using any loop
Solution:
int n,v,ans; cin>>n>>v; if((n-1)<=v){ cout<<n-1<<endl; } else{ ans=((n-v)*(n-v)+(n+v))/2-1; cout<<ans<<endl; }In problem 1D, why we can just multiply f(n,edges+1)? Why it calculates all the cases? And I think that in each tree of these forests, we choose a vertex with the minimum index as a root, and connect edges+1 roots to a path from a to b. Is my understanding right?
Yes, but you missed a A(n - 2, edges - 1) part. At the beginning for fixed edges we choose roots of each of edges - 1 tree (for the first and the last tree roots are a and b) in A(n - 2, edges - 1) ways, then we calculating number of forests, in which chosen vertices are in different trees. It's easy to see that for any v1, v2... vedges + 1 the number of forests, where vertices 1, 2, ... edges + 1 are roots and they are in different trees, equals to the number of forests where vertices v1, v2, ... vedges + 1 are roots and they are in different trees.
I get it, thanks for your explanation:)
Sorry, I still don't understand it. Would you explain more? I think the number of forests, where vertices 1,..., edges+1 are roots and they are in different trees, is not equal to f(n, edges+1). It doesn't make that vertex 1 and vertex 2 are in different trees. Thanks.
In other words, Can the everyone of f(n, edges+1) guarantee that vertex a and vertex b are in different trees?
You miss one thing, where the meaning of f(n,k) has ensured that 1,2,...,y in different trees. You can try to count f(4,2)=8. 1,2-3-4 1,2-4-3 1,3-2-4 1-3,2-4 1-4,2-3 1-3-4,2 1-4-3,2 4-1-3,2
can anyone please explain why in Div2 problem C the "cnt[1][0] = 1;" is set to 1? I'm not able to get the logic here
pref0 = 0
And why is that, still not clear, can you please explain
take the second example given in the question try with/without cnt[1][0]=1 the answer will differ because without cnt[1][0] you will miss (1,4) pair.
Got it, to count the subarrays which start from the start of the actual array we add a zero to the beginning. Thanks!!
Let us say you have a sequence of
3 2 2 3 7 6. Now a pair say (i,j) will be of even length if both i and j are either even or both are odd. Now we have to find even length subsequences whose XOR is 0. Nowcnt[0][x]stores count of all x at even index , now after doing XOR operation on an array element say a[i] if we get x and ifiis even. It means all elements which between current element when we get thisxand when we got a previousx, there XOR is 0 and this a[i] can form subsequence with all the previous number where we gotxafter XOR operation. Therefore we add it to answer and increment the count ofcnt[0][x]so that it can be used for any otherxwhich we can encounter later in array. Hope it clears your doubt.In the Question: Sasha and a Bit of relax, in the Author's code, what is the use of cnt[1][0] = 1. Can anyone explain
Pref0-1 = Pref-1 And -1 is Odd.
For Div2 C what is L and R. Are they index of arrays or values between which we have to apply xor operation?
They are indices
But in sample test case 2 how can 6 be a index in an array of 6 numbers?
"The second line contains n integers a1,a2,…,an"
The problem is written using 1-based indexing.
How can L and R be the indices of array in DIV2 C? How can 6 be index of array of 6 elements ?I am unable to find what are L and R.
Indices are 1-based in problem description.
if that's 1-based indexing then r-l+1 should be even for r,l be (odd,even) or (even,odd). Right?
Yes.
Very nice to see a contest on the weekend : ), i hope there will be much more. Thank you.
I think I have a better solution for problem B (or main-tests are weak!) I guess that for every member of array (a[i]), the divisor of it that lead us to minimum (so we divide a[i] on it and multiply our minimum member of array to it) is the divisor that is nearest to square root of a[i]. so we can first sort the array, and then for every member of the array iterate back from sqrt(a[i]) to 1 and when we see a divisor of a[i] calculate the Delta that choosing it gives us. But I couldn't prove my conjecture. Anybody can help? I think the order will be O(n.sqrt(a[i])). Sorry for bad English.
Am I the only one who wonders how could several people solve Div. 2 C / Div. 1 A in only 2 minutes? Really, there is quite a bit of thinking and coding in this problem. And also, IMHO Div. 2 D is easier than Div. 2 C, I solved them for 10 and 30 minutes correspondingly.
why we initialize the array that count 0 for odd positions with 1? i mean why in the author's solution cnt[1][0]=1 ?
Because I you don't do it, some funny pairs that look like (1, r) won't be counted.
Proof / explanation of Div 1 B bonus solution in O(n)? Thanks for any help!
I think C is TooDificult
Yes, I didn't know about treap before. But, u know, DIV1 C can be solved in O(q^3/2) time complexity and its not that difficult.
Well...I think the "forsests" in the tutorial of 1D should be replaced by "forests".aleex
On Div2D / Div1B, an interesting theorem is that odd-length palindromes can never be rearranged into a different palindrome with only one cut. Bonus: Prove it :)
For example, this gets AC: http://codeforces.com/contest/1113/submission/50039408.
Thank you very much for this editorial! But, as I suspected, problem F was really too straightforward and boring. I came up with a simple greedy solution during first 10 minutes of contest, but sadly I couldn't solve it because I am still div2 and didn't participate.
Finally done with proof and implementation of Shasha and
Interesting Fact from Graph Theory(div2. F) question. One thing I am missing with the editorial is that why we have to first choose vertices on fixed path and then rerrange them? Shouldn't it be just picking up edges -1 vertices from n-2 available, and not rearranging them — (because as per question, "2 trees are distinct if there is an edge that occurs in one of them and doesn't occur in the other one. Edge's weight matters.")Div2D/Div1B can be easily solved in O(N), where N is the string length.
First, consider the cases where it is impossible. It is impossible iff: N is even and all the characters are the same, or N is odd and all characters but the center one are the same. In these cases, there is only one possible palindrome that can be formed anyway.
We show that ALL other palindromes can otherwise be solved in 2 cuts. There exists an i such that the prefix of i characters is different from the suffix of i characters. Cut off the prefix and suffix and notice that the remaining string is still a palindrome. Simply switch the places of the prefix and suffix and we get a different palindrome from what we started with. We know that i exists, because otherwise it would reduce to the impossible case.
Now, we identify the palindromes that can be done in 1 cut. I will use B to denote some string, then B' to denote its reverse. Notice that if B ≠ B', then B'B and BB' are distinct palindromes. Similarly, if we have BB'BB', we can use 1 cut to slice off the last B' and then place it at the beginning, which gives us B'BB'B, a different palindrome. If a string can be decomposed as a series of BB'BB'... BB', with B ≠ B', then it can be solved in 1 cut. A string canNOT be decomposed in such a matter if its length is odd; then, there would be some central pivot.
We thus implement a recursive function. If N is odd, then it definitely cannot be solved in one cut. If N is even, we check if the left half equals the right half. If they are not equal, we return true. If they are, we recurse on one of the halves to see if that can be decomposed (and since the two halves are equal, if one of them can, the other can too).
Naive string comparison of the left and right half is O(N), so the total work done is at most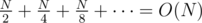 . This can be reduced to
. This can be reduced to 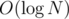 by using hashing for string comparison, but reading the input is O(N) anyway.
by using hashing for string comparison, but reading the input is O(N) anyway.
To summarize, check if this palindrome is solvable. If it is, check if it can be done in 1 cut. If it cannot, then it can be done in 2 cuts.
wtfrick this is
Is it possible to do Div2B if you are allowed to execute the operation as many times as you want?
In problem div1A we can say that if we divide the segment into two groups made up of any element and of any size will have same xor value.
D1F can also be solved using DnC and rollbackable DSU in $$$O(n \cdot m \cdot log^2{(n\cdot m)})$$$.
Implementation: link