Greetings Codeforces community! You are all invited to CodeChef’s February Cook-Off sponsored by ShareChat. The Cook-Off is a short contest that lasts 2.5 hours and features 5 problems for you to try and solve. The contest problem statements are available in English, Hindi, Bengali, Russian, Mandarin and Vietnamese.
ShareChat — India’s fastest growing social network is offering exciting jobs and internships to the participants of the Cook-Off. Visit the contest link for more details.
I hope you will join your fellow programmers and enjoy the contest problems. Joining me on the problem setting panel are:
- Tester: Deemo (Mohammad Nematollahi)
- Editorialist: Pepe.Chess (Hussain Kara Fallah)
- Statement Verifier: Xellos (Jakub Safin)
- Setters: kingofnumbers (Hasan Jaddouh), deva2802 (Devanshu Agarwal), Pi-nan (Shivam Gor), Abhinav Jain
- Mandarin Translator: huzecong (Hu Zecong)
- Vietnamese Translator: Team VNOI
- Russian Translator: Mediocrity (Fedor Korobeinikov)
- Bengali Translator: solaimanope (Mohammad Solaiman)
Hindi Translator: Akash Shrivastava
Contest Details:
- Start Date & Time: 17th February 2019 (2130 hrs) to 18th February 2019 (0000 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone
- Contest link: https://www.codechef.com/COOK103
- Registration: You just need to have a CodeChef handle to participate. For all those, who are interested and do not have a CodeChef handle, are requested to register in order to participate.
- Prizes: Top 10 performers in Global and Indian category will get CodeChef laddus, with which the winners can claim cool CodeChef goodies. Know more here: https://www.codechef.com/laddu
(For those who have not yet got their previous winning, please send an email to [email protected])
Good Luck!
Hope to see you participating!!
Happy Programming!!











The contest starts in 3.5 hours
Auto comment: topic has been updated by deva2802 (previous revision, new revision, compare).
How do you solve EVILAND?
How to solve Evil Land?
My solution: find the periodicity of F (i.e. ) then get the LCM of the periodicity of each Ai. Finally, remove elements from A which have (in their periodicity) a prime with power larger than the power of the same prime in the periodicity of F (try for each prime in F).
) then get the LCM of the periodicity of each Ai. Finally, remove elements from A which have (in their periodicity) a prime with power larger than the power of the same prime in the periodicity of F (try for each prime in F).
This gave TLE because I find the periodicity in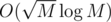 for each number.
for each number.
Why does taking the LCM help? I'm not able to understand what's going on.
If a number X has a periodicity P on a modulo M then Xi will equal all numbers Y such that Y has a periodicity Q where Q is a divisor of P. If two numbers a and b have a periodicity Pa and Pb then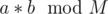 has a periodicity of LCM(Pa, Pb).
has a periodicity of LCM(Pa, Pb).
So the problem is now to remove some elements of A such that the LCM of their periodicity of the remaining is not a multiple of the periodicity of F.
To prove that, let X be a number which has a periodicity P and Xi equals Y which has a periodicity of Q. Then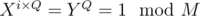 . Then
. Then 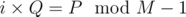 , which means that Q is a divisor of P. Remember that both P and Q are divisors of M - 1 because Xφ(M) = 1.
, which means that Q is a divisor of P. Remember that both P and Q are divisors of M - 1 because Xφ(M) = 1.
When will the problems be available for practice?
EVILAND: g(x, MOD) = periodicity of x in mod MOD. Make a[i] = g(a[i], MOD) and now the problem is removing some elements so that the lcm of the remaining elements isn't a multiple of g(F, MOD). Didn't submit because I started the contest in the last hour but I'm pretty sure this is correct. To prove this, transform multiplication to addition with a primitive root and the problem is the same but with addition.
How to solve TWOARR without persistent implicit treap or lazy updates with persistent seg tree? I solved it using lazy update with persistent seg tree but my constant was complete shit and it barely passed the TL with log^2 updates/queries.
I did the same in EVILAND but got TLE.
For TWOARR: sqrt-decomposition passed in ~2seconds
You can preprocess the primes and find periodicity in log^2 like this
It solves each case in O(N*log^2).
Setter code for TWOARR was n*log^2 . It passes in 1.8sec.
There exist sqrt deco solutions too.
How would you handle the queries using sqrt decomposition? especially the query of the first type.
Decompose array A, into root(n) blocks, then every query of type two can be handled in O(root(n)logn), using a flag to rebuild a block. For this we need to maintain a persistent seg tree on B. adjusting the Block size gives O(nroot(nlogn)) solution.
Yeah. Thought the same. just idea of persistent to handle the update of the value of b slipped out of my mind. Thanks.
what is persistent st?
Thanks for the problem, got my lazy ass to finally code persistent random BST. https://www.codechef.com/viewsolution/23140693 O(N * logN) expected time solution.
hey u coded treap . whats the difference between persistance tree and treap are both same
They aren't. Persistent treap doesn't really work because expected height breaks when you merge a treap with itself (due to how priorities work in treaps) but you can use a different randomization during merge (that I really can't explain why it works other than it makes every node have the same probability of being the root in a subtree). This different randomization is leftSide function in my code, I think you can't call this a treap anymore since it doesn't have heap properties.
For EVILAND I found primitive root and all its degrees, and sorted that information, that allows to find the discrete log for each number in O(1), giving MlogM + N overall, which passed for me
what is primitive root. and what is discrete log
I don't know, I just googled it!
ok
Almost a week since the contest and I still can't find the EVILAND editorial.