1174A - Ehab Fails to Be Thanos
If all elements in the array are equal, there's no solution. Otherwise, sort the array. The sum of the second half will indeed be greater than that of the first half.
Another solution is to see if they already have different sums. If they do, print the array as it is. Otherwise, find any pair of different elements from different halves and swap them.
Code link: https://pastebin.com/FDXTuDdZ
1174B - Ehab Is an Odd Person
Notice that you can only swap 2 elements if they have different parities. If all elements in the array have the same parity, you can't do any swaps, and the answer will just be like the input. Otherwise, let's prove you can actually swap any pair of elements. Assume you want to swap 2 elements, $$$a$$$ and $$$b$$$, and they have the same parity. There must be a third element $$$c$$$ that has a different parity. Without loss of generality, assume the array is $$$[a,b,c]$$$. You'll do the following swaps:
- Swap $$$a$$$ and $$$c$$$: $$$[c,b,a]$$$.
- Swap $$$b$$$ and $$$c$$$: $$$[b,c,a]$$$.
- Swap $$$a$$$ and $$$c$$$: $$$[b,a,c]$$$.
In other words, you'll use $$$c$$$ as an intermediate element to swap $$$a$$$ and $$$b$$$, and it'll return to its original position afterwards! Since you can swap any pair of elements, you can always sort the array, which is the lexicographically smallest permutation.
Code link: https://pastebin.com/xhqGXLiu
Time complexity: $$$O(nlog(n))$$$.
1174C - Ehab and a Special Coloring Problem
Let's call the maximum value in the array $$$max$$$. Let the number of primes less than or equal to $$$n$$$ be called $$$p$$$. Then, $$$max \ge p$$$. That's true because a distinct number must be assigned to each prime, since all primes are coprime to each other. Now if we can construct an answer wherein $$$max=p$$$, it'll be optimal. Let's first assign a distinct number to each prime. Then, assign to every composite number the same number as any of its prime divisors. This works because for any pair of numbers $$$(i,j)$$$, $$$i$$$ is given the same number of a divisor and so is $$$j$$$, so if they're coprime (don't share a divisor), they can't be given the same number!
Code link: https://pastebin.com/tDbgtnC8
Time complexity: $$$O(nlog(n))$$$.
1174D - Ehab and the Expected XOR Problem
The main idea is to build the prefix-xor of the array, not the array itself, then build the array from it. Let the prefix-xor array be called $$$b$$$. Now, $$$a_l \oplus a_{l+1} \dots \oplus a_r=b_{l-1} \oplus b_{r}$$$. Thus, the problem becomes: construct an array such that no pair of numbers has bitwise-xor sum equal to 0 or $$$x$$$, and its length should be maximal. Notice that "no pair of numbers has bitwise-xor sum equal to 0" simply means "you can't use the same number twice". If $$$x \ge 2^n$$$, no pair of numbers less than $$$2^n$$$ will have bitwise-xor sum equal to $$$x$$$, so you can just use all the numbers from 1 to $$$2^n-1$$$ in any order. Otherwise, you can think of the numbers forming pairs, where each pair consists of 2 numbers with bitwise-xor sum equal to $$$x$$$. From any pair, if you add one number to the array, you can't add the other. However, the pairs are independent from each other: your choice in one pair doesn't affect any other pair. Thus, you can just choose either number in any pair and add them in any order you want. After you construct $$$b$$$, you can construct $$$a$$$ using the formula: $$$a_i=b_i \oplus b_{i-1}$$$.
Code link: https://pastebin.com/0gCLC0BP
Time complexity: $$$O(2^n)$$$.
1174E - Ehab and the Expected GCD Problem
Let's call the permutations from the statement good. For starters, we'll try to find some characteristics of good permutations. Let's call the first element in a good permutation $$$s$$$. Then, $$$s$$$ must have the maximal possible number of prime divisors. Also, every time the $$$gcd$$$ changes as you move along prefixes, you must drop only one prime divisor from it. That way, we guarantee we have as many distinct $$$gcd$$$s as possible. Now, there are 2 important observations concerning $$$s$$$:
Observation #1: $$$s=2^x*3^y$$$ for some $$$x$$$ and $$$y$$$. In other words, only $$$2$$$ and $$$3$$$ can divide $$$s$$$. That's because if $$$s$$$ has some prime divisor $$$p$$$, you can divide it by $$$p$$$ and multiply it by $$$4$$$. That way, you'll have more prime divisors.
Observation #2: $$$y \le 1$$$. That's because if $$$s=2^x*3^y$$$, and $$$y \ge 2$$$, you can instead replace it with $$$2^{x+3}*3^{y-2}$$$ (divide it by $$$9$$$ and multiply it by $$$8$$$), and you'll have more prime divisors.
Now, we can create $$$dp[i][x][y]$$$, the number of ways to fill a good permutation up to index $$$i$$$ such that its $$$gcd$$$ is $$$2^x*3^y$$$. Let $$$f(x,y)=\lfloor \frac{n}{2^x*3^y} \rfloor$$$. It means the number of multiples of $$$2^x*3^y$$$ less than or equal to $$$n$$$. Here are the transitions:
If your permutation is filled until index $$$i$$$ and its $$$gcd$$$ is $$$2^x*3^y$$$, you can do one of the following $$$3$$$ things upon choosing $$$p_{i+1}$$$:
Add a multiple of $$$2^x*3^y$$$. That way, the $$$gcd$$$ won't change. There are $$$f(x,y)$$$ numbers you can add, but you already added $$$i$$$ of them, so: $$$dp[i+1][x][y]=dp[i+1][x][y]+dp[i][x][y]*(f(x,y)-i)$$$.
Reduce $$$x$$$ by $$$1$$$. To do that, you can add a multiple of $$$2^{x-1}*3^y$$$ that isn't a multiple of $$$2^x*3^y$$$, so: $$$dp[i+1][x-1][y]=dp[i+1][x-1][y]+dp[i][x][y]*(f(x-1,y)-f(x,y))$$$.
Reduce $$$y$$$ by $$$1$$$. To do that, you can add a multiple of $$$2^x*3^{y-1}$$$ that isn't a multiple of $$$2^x*3^y$$$, so: $$$dp[i+1][x][y-1]=dp[i+1][x][y-1]+dp[i][x][y]*(f(x,y-1)-f(x,y))$$$.
As for the base case, let $$$x=\lfloor log_2(n) \rfloor$$$. You can always start with $$$2^x$$$, so $$$dp[1][x][0]=1$$$. Also, if $$$2^{x-1}*3 \le n$$$, you can start with it, so $$$dp[1][x-1][1]=1$$$. The answer is $$$dp[n][0][0]$$$.
Code link: https://pastebin.com/N8FRN9sA
Time complexity: $$$O(nlog(n))$$$.
1174F - Ehab and the Big Finale
Let $$$dep_a$$$ be the depth of node $$$a$$$ and $$$sz_a$$$ be the size of the subtree of node $$$a$$$. First, we'll query the distance between node 1 and node $$$x$$$ to know $$$dep_x$$$. The idea in the problem is to maintain a "search scope", some nodes such that $$$x$$$ is one of them, and to try to narrow it down with queries. From this point, I'll describe two solutions:
HLD solution:
Assume that your search scope is the subtree of some node $$$u$$$ (initially, $$$u$$$=1). How can we narrow it down efficiently? I'll pause here to add some definitions. The heavy child of a node $$$a$$$ is the child that has the maximal subtree size. The heavy path of node $$$a$$$ is the path that starts with node $$$a$$$ and every time moves to the heavy child of the current node. Now back to our algorithm. Let's get the heavy path of node $$$u$$$. Assume its other endpoint is node $$$v$$$. We know that a prefix of this path contains ancestors of node $$$x$$$. Let the deepest node in the path that is an ancestor of node $$$x$$$ be node $$$y$$$ (the last node in this prefix). I'll now add a drawing to help you visualize the situation.
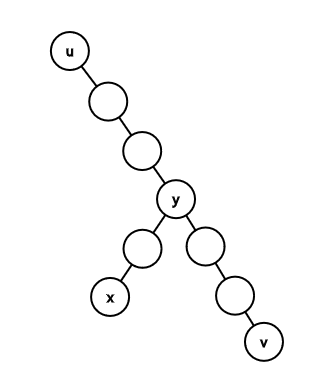
So, recapping, $$$u$$$ is the root of your search scope, $$$v$$$ is the endpoint of the heavy path starting from $$$u$$$, $$$x$$$ is the hidden node, and $$$y$$$ the last ancestor of $$$x$$$ in the heavy path. Notice that $$$y$$$ is $$$lca(x,v)$$$. Now, we know that $$$dist(x,v)=dep_x+dep_v-2*dep_y$$$. Since we know $$$dep_x$$$, and we know $$$dep_v$$$, we can query $$$dist(x,v)$$$ to find $$$dep_y$$$. Since all nodes in the path have different depths, that means we know $$$y$$$ itself!
Now, if $$$dep_x=dep_y$$$, $$$x=y$$$, so we found the answer. Otherwise, we know, by definition, that $$$y$$$ is an ancestor of $$$x$$$, so it's safe to use the second query type. Let the answer be node $$$l$$$. We can repeat the algorithm with $$$u=l$$$! How long will this algorithm take? Note that $$$l$$$ can't be the heavy child of $$$y$$$ (because $$$y$$$ is the last ancestor of $$$x$$$ in the heavy path), so $$$sz_l \le \lfloor\frac{sz_y}{2} \rfloor$$$, since it's well-known that only the heavy child can break that condition. So with only 2 queries, we managed to cut down at least half of our search scope! So this algorithm does no more than $$$34$$$ queries (actually $$$32$$$ under these constraints, but that's just a small technicality).
Code link: https://pastebin.com/CM8QwdUf
Centroid decomposition solution:
As I said, assume we have a search scope. Let's get the centroid, $$$c$$$, of that search scope. If you don't know, the centroid is a node that, if removed, the tree will be broken down to components, and each component's size will be at most half the size of the original tree. Now, $$$c$$$ may and may not be an ancestor of $$$x$$$. How can we determine that? Let's query $$$dist(c,x)$$$. $$$c$$$ is an ancestor of $$$x$$$ if and only if $$$dep_c+dist(c,x)=dep_x$$$. Now, if $$$c$$$ is an ancestor of $$$x$$$, we can safely query the second node on the path between them. Let the answer be $$$s$$$, then its component will be the new search scope. What if $$$c$$$ isn't an ancestor of $$$x$$$? That means node $$$x$$$ can't be in the subtree of $$$c$$$, so it must be in the component of $$$c$$$'s parent. We'll make the component of $$$c$$$'s parent the new search scope! Every time, the size of our search scope is, at least, halved, so the solution does at most $$$36$$$ queries.
Code link: https://pastebin.com/hCNW5BfQ










Does anyone have other approach for E, though editorial is well explained.
F i heard HLD first time, also don't know CD. what are they ?
HLD — Heavy Light Decomposition CD — Centroid Decomposition
I have submitted an O(n) solution for E using casework and simple counting principles. However, I think doing all the thinking required to get this solution functional is much harder than mindlessly typing a DP solution, so such an approach may not be so viable in contest unless O(nlogn) is too slow.
I did E without dp. I made a list of possible gcd sequences that looked something like this: [(2^(k+1), …, 8, 4, 2, 1), (3 * 2^k, …, 12, 6, 3, 1), (3 * 2^k, …, 12, 6, 2, 1), …, (3 * 2^k, 2^k, …, 8, 4, 2, 1)] (i.e. progressing by 2 for each gcd, except for maybe once progressing by 3). Then for each gcd list: g, use combinatorics to count how many ways to place multiples of g[0], then multiples of g[1], ...
Did you hardcode these lists in the code? Besides, there could be like 20 lists.
Can you explain that for any given list, how to calculate the number of corresponding permutations ? erickjohnross
No, I did not hardcode these lists, I had a loop that determined where the factor of 3 would be used. You can check out my submission: https://codeforces.com/contest/1174/submission/55937662
For the combinatorics, suppose that for each element in the gcd list, we keep track of (e,f): how many numbers have that gcd as a factor (but not any larger gcd factors), and also how many slots we have to put them into (i.e. how many numbers have not been placed so far). We can then count how to place all the numbers starting from the largest gcd down to the smallest. For each gcd, one of the e numbers must be placed in the first available slot in order for that gcd to actually appear. There are e ways to choose which number this is. Then we can place the remaining e-1 numbers into any of the f-1 slots. There are (f-1)P(e-1) ways to do this, where nPk is the permutation function. So the total number of ways to place a gcd group is e * (f-1)P(e-1).
.
Lightning fast editorials! Love it!
Anyone else got their problem B hacked? I didn't understand why my solution is wrong. My submission. Any help would be appreciated.
If there are only even numbers you can’t sort.There must be at least one odd and one even number in such case you are able to swap everything you want.
Why u put exactly 36 queries, not round to 40?. The complexity of the search will be the same, but you save people from getting WA by one or two additional queries.
During the contest, I also came up with a solution using Centroid decomposition approach like in editorial, but I was scared to write it. Because the simple analysis gave me 37 queries. n = 2 ** 18, so we need 18 * 2 = 36 queries for the main approach and additional query for querying root to find the height of the node. Probably we need only 35, but I decided not to spend time to figure it and write another solution.
I didnt got WA. But I always hate keeping exact queries. There should be a lose upperbound.
Like in last Global round C we had $$$5*n$$$ instead of $$$4*n$$$. There should be something lose. Lose depends on author.
But penalising for 1-2 extra queries without any reason imo is bad.
I'm sorry, I didn't give it much thought. My solution does $$$34$$$ queries in simple analysis and $$$32$$$ in practice, so I thought $$$36$$$ isn't strict at all. The centroid decomposition solution is by the testers.
It's your problem man, you don't have to sorry anyone. Some people like to do easy things which still make them feel like they are good
I tried Centroid Decomposition after the competition and got AC, never heard of CD until I read the editorial, mine needed all 36 queries on test #16 and alot of the tests it passed with 35 queries. And I think at first I tried with getting first centroid from root and starting there and got WA, but then changed to starting from successor from root (i.e. "s 1" as first query) then proceed from that, then it passed, just barely. But I'm sure because I don't understand everything fully someone who knew what they were doing probably could have shaved a query or two off.
can somebody explain problem D? where are pairs? which pairs? what pairs? i just don't understand that part
n<=18
yeah, i made mistake, can you answer updated version of my question?
The pair of numbers whose xor is x
Got it!
Lets say for n = 3 and x = 6, (2,4) make a pair whose xor is 6. So you are saying 4 and 2 cant be in one array because b[i] xor b[j] = x. Consider this array.
[ 4 , 1 , 2]
I dont think any prefix xor will be equal to 6. And I think this is a valid array. Can you explain this ? I am still in doubt.
I think you have mistaken the array b (which is the prefix-xor array) and the array a we want to build as the answer. We use b to build a.
So as your example : [4, 1, 2] is a not b. The condition of one number each pair in b must be satisfied so a can be built correctly. (a[i] = b[i] xor b[i-1] )
Hope you will understand it
Thanks It Helped
n is 18 2^18 around 2e5 which pass in 1 sec
why from 1 to 2^n — 1 ?
Because $$$ 1 \leq a_i \lt 2^n $$$
Why do not I have this code running on problem C?
You haven't handled the primes greater than $$$\sqrt{100000}$$$.
understand, it was a mistake, I copied the sieve and did not notice i * i in place of i
In problem C its given that any pair (i,j) if its coprime than ai!=aj....then how 1 2 1 is satisfying this condition?? as 1 and 1 are coprime and also equal..i think i misuderstood the question pls help!
i and j, not a[i] and a[j]
You haven't the if(prime[j]) continue;
thanks for the lightning fast editorial :)
can somebody explain problem D? where are pairs? which pairs? what pairs? i just don't understand that part
In Question A how will you maintain the order while simply sorting and printing the array?
The point is not to maintain the order, but to keep the same elements and rearrange them so the sum of the first half won't be equal to the second.
By sorting them, you will definitely get array where the second half is greater than the first if all the elements are not the same. If they all have the same value you can't rearrange them to get diferent sums, so the answer will be (-1).
but in question itself it is written You are allowed to not change the order.
I understand, the wording of the description is not well written. Also, it is not written that when the output can have mutiple reorderings print any of them.
So to answer your reply, the statement means that if the initial ordering have different sums then print the initial not reordered solution.
Also, another remark is that it never says if the initial ordering will always have same sums.
"You are allowed to not change the order."
Is not the same as
"You are not allowed to change the order."
The first version simply means you can change the order if you'd like, but that is not required.
I too got confused with the language and thought that the relative order must be maintained as it is .
Did anyone pass E with $$$N log ^2 N$$$ solution? Or it was intentionally eliminated?
My randomized solution to F (which imo has a very low probability of failure):
1) Randomly choose a node U from V and use Query 1 on it to find distance D of X from it.
2) The LCA of U and X must be at a distance of D/2 from U, so walk D/2 distance up from U.
3) Use Query 2 on the current node to find the subtree X belongs to, and discard all the candidate nodes that lie outside it.
I had the same solution, but without the randomization. It failed on Test 99. But adding randomization made it pass. While it is kinda intuitive as to why it works, I really want to understand what is the exact difference it makes.
There is another approach for F. First query for the distance from root to node x to find the level of node x. The nodes in this level are our primary search scope. Now we will reduce the search scope by half using no more than 2 queries. Sort the nodes of search scope by their dfs starting time. Let u be the middle node of this order. Now we query for the distance from u to x. Using the distance we can find the LCA of u and x. Let the LCA be v. Now we query the 2nd type for this node v and the updated search scope is either the left or the right half of the initial search scope.
How would you find the LCA of u and x using the distance? I saw your code and you've assumed that the LCA's at a distance of the distance between the 2 nodes/2 from the depth of our target node. How would you prove this? Also it isn't always guaranteed that the middle node of your dfs order will be at the same depth as your target node, right?
Notice that all the candidates nodes are at the same level. We know the level after just first query.
I'm confused as to why taking the midpoints of the dfs order would give a node with the same depth as a candidate node (if I've understood your solution correctly)
We are considering nodes of that level only, then sort the nodes according to their dfs order.
When I read your solution I started wondering why we can always reduce the search scope by at least half. I came up with the following argument: Assume that our search scope in some step is the ordered list s. Let s' denote our search scope after one iteration of your procedure (i.e. those 2 queries you proposed). Note that all the elements of s' have to appear consecutive in s. This is because s' contains exactly those nodes of s with ancestor a, where a is the response we get from the second query (i.e. a is the second node on a path from v to x). If the elements of s' were not consecutive in s then there would be some node p in s such that p is not in s' but p has ancestor a (Because we sorted after dfs starting time). Now assume for a contradiction that $$$2 \cdot |s'| > |s|$$$. Because the nodes in s' appear consecutive in s it follows that u is in s'. But then u would have ancestor a and thus $$$LCA(u, x) = a \neq v$$$. This is a contradiction.
Editorial code of D is wrong as it doesn't output right ans for second test case. 2 4
Expected output :- 3 1 3 1
Output by editorial code :- 2 3 1
The whole segment is one of the subsegments.
3 ^ 1 ^ 3 ^ 1 = 0
EDIT: Sorry, in the first place, editorial's solution outputs 3 [1, 3, 1] ; expected answer.
first no. is the size of array. its not 3 1 3 1 size of array 3 element:- 1 3 1
My bad. Please check whether the code you run is certainly editorial's. (Or possibility like swapped with your solution.)
I think that I have the correct code. For confirming that you can check it owm your own.
????
hmm.. Inputs are also correct?
Please simply run the code below. (wrote input data directly)
Or, to avoid depending on the environment, please check this https://wandbox.org/permlink/9PBeIfBz5Yjsqzl2
According to the editorial, how it can be proved that this length is maximized. I mean is there any possibility to make new elements with the prefix[i-2], prefix[i-1] and prefix[i] or something like that.
If we take full subset {3,1,3,1}, and the xor value of those elements would be zero. So your input is wrong.
I am one of the victims of test 99 in F, XD
But I don't get in which case my solution goes over the query limit. It's easy to follow the code (probably), else I'll clarify.
Your solution is similar to mine (55049717)
If someone can explain why does this approach fail, or perhaps give a hint on what is the tree like in test 99, I would really appreciate it.
I think that the tree might be of the type as the example below:
10 10
1 2 2 3 3 4 1 5 5 6 6 7 5 8 8 9 8 10
My solution is also the same. I tested my code with this case:
200000
1 2
2 3
3 4
...
...
...
199999 200000
and this gives RUNTIME ERROR while traversing through the DFS. Don't know what's the reason! :/
"ulimit -s unlimited" should help
How to use it in Windows OS. Can you please explain?
I have no idea. Google-search Stack limit Windows
Actually, this is for Linux. I use Windows.
This is a blog for Windows OS that can help: https://codeforces.com/blog/entry/15874 Anyway Thanks! :)
Counter TC
I probably figured out, for a tree like this (of larger size) -
the number of queries in the worst case (when the rightmost leaf is the secret node) will go over 500, hitting the 'second type of query' for every node in the rightmost branch of the tree.
Brilliant round!!!
Problem E why the first number has to be 2^x*3^y? Any number in the form 2^x has more divisors than 2^x*3^y or not?
I do not understand that part either
Consider n = 12 here 2^3 and (2^2)*(3^1) both have maximum prime factors so we need to consider both.
Thank you! now I got it (:
Hey! Why is this code failing on problem A?
include"bits/stdc++.h"
using namespace std; int main(){ int n;
}
mohammedehab2002 In the dp (PROBLEM E) where you are explaining the transitions, you said that "but you already added i" so you subtracted it from the product, Why not in the others transitions??
In the first kind of transitions, we add a number that's a multiple of $$$2^x*3^y$$$. We used $$$i$$$ of them because the $$$gcd$$$ is $$$2^x*3^y$$$, so all already added numbers are of this kind. However, in the second kind of transitions, we add a number of the form $$$2^{x-1}*3^z$$$ (for some $$$z$$$). We never used any of these numbers since the power of $$$2$$$ in the $$$gcd$$$ is $$$x$$$.
In F random works fine!
https://codeforces.com/contest/1174/submission/55052166
nvm, I'm stupid, 36/2=18. :X
E can be solved in $$$O(n)$$$
Let $$$k=\lfloor \log_2 n \rfloor$$$, $$$dp0[i][j]$$$ be the number of "good sequence" with length $$$j$$$ and gcd $$$2^i$$$, $$$dp1[i][j]$$$ be the number of "good sequence" with length $$$j$$$ and gcd $$$2^{i-1}\cdot 3$$$.
For each $$$0 \le i \le k$$$, it's obvious that $$$1 \le j \le \frac{n}{2^i}$$$, so the total number of valid state is less than $$$n + \frac{n}{2} + \frac{n}{4} + \cdots + 1 = O(n)$$$.
Since each value of $$$dp$$$ can be calculated in $$$O(1)$$$, the time complexity is $$$O(n)$$$.
55054749
I tried reading the editorial for problem E, however I don’t understand why in the first observation we get more prime divisors if we divide by $$$p$$$ and multiply by 4?
That's the case when p >= 5 , means we will only consider the numbers having 2 or 3 in its factorization
In the editorial it is written prime divisors, but I think that they mean all divisors
It is prime divisors only... If a number is n = 7*(2^x)*(3^y) then here 7 is a prime divisor which is greater than 3.. so we have better choice of n , n = 4 * (2^x) * (3^y) = (2^(x+2))*(3^y)
Initially n had x+y+1 prime factors.. but we can have x+y+2..
I didnt notice that you count same prime number more times, I understand it now, thanks
In Problem D-
There is no non-empty subsegment with bitwise XOR equal to 0 or x,
A sequence b is a subsegment of a sequence a if b can be obtained from a by deletion of several (possibly, zero or all) elements from the beginning and several (possibly, zero or all) elements from the end.
Construct an array such that no pair of numbers has bitwise-xor sum equal to 0 or x, and its length should be maximal
How this satisfies above criteria?
I guess that by pair of numbers in the last definition they mean range of numbers between two indexes
The array which is mentioned here is the prefix xor of answer array (and not the answer array) means , prefix[i] = a[1]^a[2]..^a[i]
If the answer array has any subsegment from l to r which gives xor as 0 or x. Then in prefix array , prefix[l]^prefix[r-1] will give 0 or x. That's why it's said that no pair in prefix array gives 0 or x as their XOR.
Problem F can be done without HLD or Centroid decomposition.
code
The main idea is that: if $$$h[v]$$$, $$$h[x]$$$ — distances from the root to vertexes $$$v$$$ and $$$x$$$ and we ask query of the first type about $$$v$$$. We can find LCA for $$$v$$$ and $$$x$$$. Denote by $$$p$$$ the LCA. Now ask query of the second type about $$$p$$$. Denote by $$$u$$$ the answer. Now let's solve the problem for subtree of $$$u$$$.
If we write down all the leaves of the tree in dfs order $$$v_1, \dots, v_k$$$, and choose $$$v_{k/2}$$$ as v, we reduce our problem to problem at least twice less. So number of questions is not greater that $$$2logn$$$
In problem F I am getting wrong answer on test 99, can anyone help me? Here is the link to my code: https://codeforces.com/contest/1174/submission/55057721 Thanks!!
what should i modify in this code https://codeforces.com/contest/1174/submission/55049051 problem C can anyone help ?
You assign 2 to numbers that are not even or prime but as an example 25 and 21 are not both but you assigned their value to 2 .they are coprime and can not be equal. You should assign each number and its multiples to the same number.
Can anyone explain me the solution of C?..thanks.
Great explanation..now I understand it... Thanks
Why always choose first divisor?? And in editorial it is given to choose only prime divisor but I think if we choose composite then it also works.? Correct me if I'm wrong..thanks
thanks @HynDuf great explanation
fast and useful,thx!:)
Actually problem F could be solved using binary search and binary lifting and binary search.
First just save the nodes according to their height(their distance from the root), and for each height, save the nodes according to dfs order. So query "d 1" will narrow the search down to the set of nodes which have the same height.
Let h[v] is the distance from the root to v. Obviously h[1] = 0.
Let dist[v] is the distance from the x (the hidden node) to v. Obviously dist[x] = 0.
Because in the set nodes are in dfs order, so let say x (the hidden node) is i-th node in the set, we have the following observations in the set:
a, From 1st->(i-1)-th node: dist[v] is non-increasing.
b, The i-th node is x and dist[x] = 0.
c, From (i+1)-th -> final node : dist[v] is non-decreasing.
<--Look like the upper envelope so we can perform binary search somehow in the set -->
Suppose we get into the range [l, r] in the set, let mid = (l+r)/2. Let the mid-th node in the set is v. Query dist[v] ("d {v}" obviously).
Obviously if(dist[v] == 0) the answer is x == v. We can see that we will always get to know x while performing binary search
Because h[v] = h[x] so dist[v] is even, and by binary lifting, we could find the u, the (dist[v]/2)-th parent of v, which is also of x. Then we query ("s {u}"), let say we get the node t, and obviously dist[t] = dist[v]/2 — 1. Again by binary lifting, we find z is the (dist[t])-th parent of v.
Because the nodes in any sets of same-height nodes are in dfs order, so if z is placed before t, so v is placed before x, and we move to the range [mid+1, r] to find x. Or else we move to [l, mid-1].
I think we can prove that no more that 35 queries could be used.
My submission : 55063713
can someone tell me why is my solution of B is failing: https://codeforces.com/contest/1174/submission/55029449
initialise odds and even to 0 as it will work...
Can someone please explain me what is the use of the
ex[arr[i]%2]=1;in line 13 of [this] solution of problem B (https://pastebin.com/xhqGXLiu)there are two flags if ex[0] is true that means at least one even number is present if ex[1] is true that means at least one odd number is present
for all odd numbers num%2 = 1 and even numbers num%2 = 0
but these variable may contain garbage value... it will work I compile it..
variables in global scope have default values. ex. false for booleans, and 0 for numbers.
yes u r write but in this case variable is not global so we should initialise it with 0 to avoid garbage value... correct me if I'm wrong.
I thought we were talking about ex, which is global. If we weren’t, then that’s my mistake.
but I'm talking about @v_kamani19 code
Okay... if all numbers are either even or odd then we can't swap any. This flag ensures that at least one even or one odd is present. Isn't it? Thanks!
yes that's it
Dou you guys have any idea about what is causing TLE at case 12 in Problem F? I tryed cheking the number of queries, Fast IO, wrong centroid, but i couldn`t find it. This is my code: https://codeforces.com/contest/1174/submission/55087589
Now it`s OK, I have finished the problem.
Can anybody tell me why i'm getting TLE for problem-B for this java code---
import java.util.*; import java.io.*;
public class HelloCodiva { public static void main(String[] args) throws Exception {
BufferedReader br=new BufferedReader(new InputStreamReader(System.in)); int n=Integer.parseInt(br.readLine()); String[] str=br.readLine().split(" "); int[] arr=new int[n]; int c1=0; for(int i=0;i<n;i++){ arr[i]=Integer.parseInt(str[i]); if(arr[i]%2==1){ c1++; } } if(c1!=0 && c1!=n){ Arrays.sort(arr); } for(int i=0;i<n;i++){ System.out.print(arr[i]+" "); }} }
Is array.sort O(NlogN) ?
Thanks, i just found that for object type java uses merge sort whereas for primitive types it uses quick sort, whose worst case is N2.
Good job!
in problem 1, the last line says , we cannot change the order!!! how can we apply sorting then???
Read it again ! "You are allowed to not change the order."
ok! got it dude!
Is there O(n) solution for problem E?
Can someone please explain me why do we need to take prefix xor's for problem D ? For eg. if we take case of x>=2^n, we can take the array as 1,2,3,..,2^n-1. We cannot have xor equal to 0 or x for the sequence. Then what is the need of taking prefix xor for each ? What am I missing ?
But when you take 3 first elements, then xor of this subsegment is equal to 0. If I good understood your thinking of course. :)
What do you mean by You are allowed to not change the order in problem A???
If the initial order is good, You are allowed to not change the order and just print it as an answer.
Ignore.
short questions , fast editorial , good explanation , great!
For F here is the solution I thought of. Find the level of x(say r) by quering distance from 1. Now considering the distances of all the nodes(ordered in the order of dfs traversal) at level r from x we have an array of size atmost O(n) in which there exists exactly 1 minima(the distance decrease to 0, then increase) which we can find in O(logn). Is there something I am missing because I am not even using queries of the second type.
Can someone explain what is the prefix-xor concept for problem D. I had a hard time trying to understand the editorial. Couldn't get that.
Let's call an array A and you want to find the xor in a range from l to r. To do that, you can calculate an array P (prefix-xor) as follow:
Now
answers the query To solve problem D, find P instead of A.
Why are we searching using the heaviest path rather than the longest path?
Just a lil observation on E
I think it's more accurate to say the sum of the powers on the priime divisors of s should be maximal. That way we have more powers to drop at every step. For examples it would be more optimal to take 180 that has 3 prime divisors(2, 3, 5) than to take 210 that has 4 prime divisors(2, 3, 5, 7).
I believe this is more of a clarification than an observation. The editorial meant what you just stated.
I wonder if problem E has a combinatorial solution. Because I reviewed some AC codes, and I saw other approaches ,but I could not understand them.
C can be solved in $$$O(n)$$$ by just using the way we sieve prime in $$$O(n)$$$
All you need is to add two lines to the original code
WoW, nice, I didn't even know this existed!
Can't find a test for maximum queries of my solution of F.
The idea is to keep the amount of possible vertices (i.e. places on the depth we find by first query) in a subtree of root. On every step we want to ask no more than 2 queries (it's provable we'll ask exactly one on the last step, so the max sum is 36), and change the tree (move the root or cut a part) in the way, that amount of possible vertices is at least 2 times smaller.
Let's look at the root: there're $$$W$$$ possible vertices. If it has no children with at least $$$W / 2$$$ possible vertices, then we perform an s-query and continue. Otherwise, we find first vertex $$$v$$$, which children all have possible vertices value less than $$$W / 2$$$ and perform a d-query for it. After that we know if $$$x$$$ is placed in the subtree of $$$v$$$ or not. If not we remove the whole subtree, otherwise perform an s-query from $$$v$$$.
The submission: 55134088
The most amount of queries in the system tests is 18.
I wonder if it's possible to construct a test with worse result or maybe it's provable that maximum queries if less than 36. Can anyone help?
[deleted]
Need help in E.
Why $$$f([3, 1, 2]) = 2$$$(what does $$$g_i$$$ mean?)
G[i] — gcd of the prefix of size i of the permutation, or gcd(p1,p2,p3,...,pi)
sorry, i don't understand.
for $$$[3, 1, 2]$$$
$$$g[1] = gcd(3) = 1$$$
$$$g[2] = gcd(3, 1) = 1$$$
$$$g[3] = gcd(3, 1, 2) = 1$$$
why $$$f([3,1,2])=2$$$
gcd(3) = 3, not 1 greatest common divisor of a single number is the number itself. so it will be g[1] = gcd(3) = 3 g[2] = gcd(3,1) = 1 g[3]= gcd(3,1,2)=1 We have 2 distinct gcd. Another example: for [4,2,1,3] g[1] = 4 g[2]= gcd(4,2) = 2 g[3]= gcd(4,2,1) = 1 g[4] = gcd(4,2,1,3) = 1 So we have 3 distinct gcd.
Sorry for the weird format in which the comment came out.
oh, the thing I missed is greatest common divisor of a single number is the number itself.
thank you :)
Great F, need more like this in the future.