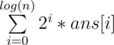1516A - Tit for Tat
The general approach to minimizing an array lexicographically is to try to make the first element as small as possible, then the second element, and so on. So greedily, in each operation, we'll pick the first non-zero element and subtract $$$1$$$ from it, and we'll add that $$$1$$$ to the very last element. You can make the implementation faster by doing as many operations as you can on the first non-zero element simultaneously, but it's not necessary.
Code link: https://pastebin.com/pBsychs2
1516B - AGAGA XOOORRR
So let's try to understand what the final array looks like in terms of the initial array. The best way to see this is to look at the process backwards. Basically, start with the final array, and keep replacing an element with the $$$2$$$ elements that xor-ed down to it, until you get the initial array. You'll see that the first element turns into a prefix, the second element turns into a subarray that follows this prefix, and so on. Hence, the whole process of moving from the initial to the final array is like we divide the array into pieces, and then replace each piece with its xor, and we want these xors to be equal. A nice observation is: we need at most $$$3$$$ pieces. That's because if we have $$$4$$$ or more pieces, we can take $$$3$$$ pieces and merge them into one. Its xor will be the same, but the total piece count will decrease by $$$2$$$. Now, checking if you can divide it into $$$2$$$ or $$$3$$$ pieces is a simple task that can be done by bruteforce. You can iterate over the positions you'll split the array, and then check the xors are equal using a prefix-xor array or any other method you prefer.
Additional idea: for $$$2$$$ pieces, you don't even need bruteforce. It's sufficient to check the xor of the whole array is $$$0$$$. Hint to see this: write the bruteforce.
Code link: https://pastebin.com/tnLpW23C
Bonus task: can you find an $$$O(n)$$$ solution? What if I tell you at least $$$k$$$ elements have to remain instead of $$$2$$$?
1516C - Baby Ehab Partitions Again
First of all, let's check if the array is already good. This can be done with knapsack dp. If it is, the answer is $$$0$$$. If it isn't, I claim you can always remove one element to make it good, and here's how to find it:
Since the array can be partitioned, its sum is even. So if we remove an odd element, it will be odd, and there will be no way to partition it. If there's no odd element, then all elements are even. But then, you can divide all the elements by $$$2$$$ without changing the answer. Why? Because a partitioning in the new array after dividing everything by $$$2$$$ is a partitioning in the original array and vice versa. We just re-scaled everything. So, while all the elements are even, you can keep dividing by $$$2$$$, until one of the elements becomes odd. Remove it and you're done. If you want the solution in one sentence, remove the element with the smallest possible least significant bit.
Alternatively, for a very similar reasoning, you can start by dividing the whole array by its $$$gcd$$$ and remove any odd element (which must exist because the $$$gcd$$$ is $$$1$$$,) but I think this doesn't give as much insight ;)
Code link: https://pastebin.com/aiknVwkZ
1516D - Cut
Let's understand what "product=LCM" means. Let's look at any prime $$$p$$$. Then, the product operation adds up its exponent in all the numbers, while the LCM operation takes the maximum exponent. Hence, the only way they're equal is if every prime divides at most one number in the range. Another way to think about it is that every pair of numbers is coprime. Now, we have the following greedy algorithm: suppose we start at index $$$l$$$; we'll keep extending our first subrange while the condition (every pair of numbers is coprime) is satisfied. We clearly don't gain anything by stopping when we can extend, since every new element just comes with new restrictions. Once we're unable to extend our subrange, we'll start a new subrange, until we reach index $$$r$$$. Now, for every index $$$l$$$, let's define $$$go_l$$$ to be the first index that will make the condition break when we add it to the subrange. Then, our algorithm is equivalent to starting with an index $$$cur=l$$$, then replacing $$$cur$$$ with $$$go_{cur}$$$ until we exceed index $$$r$$$. The number of steps it takes is our answer. We now have $$$2$$$ subproblems to solve:
calculating $$$go_l$$$
To calculate $$$go_l$$$, let's iterate over $$$a$$$ from the end to the beginning. While at index $$$l$$$, let's iterate over the prime divisors of $$$a_l$$$. Then, for each prime, let's get the next element this prime divides. We can store that in an array that we update as we go. If we take the minimum across these occurrences, we'll get the next number that isn't coprime to $$$l$$$. Let's set $$$go_l$$$ to that number. However, what if $$$2$$$ other elements, that don't include $$$l$$$, are the ones who aren't coprime? A clever way to get around this is to minimize $$$go_l$$$ with $$$go_{l+1}$$$, since $$$go_{l+1}$$$ covers all the elements coming after $$$l$$$.
counting the number of steps quickly
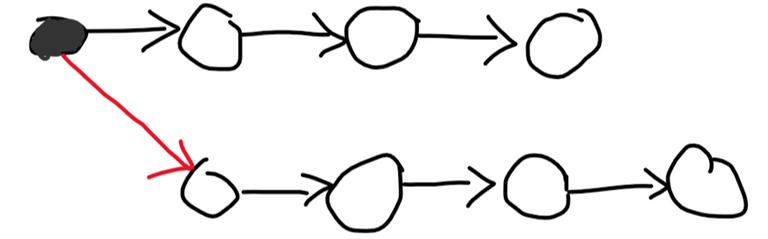
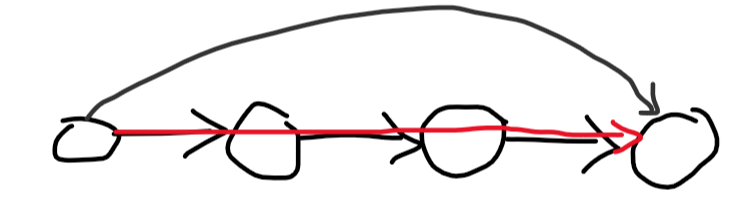
This is a pretty standard problem solvable with the binary lifting technique. The idea is to perform many jumps at a time, instead of $$$1$$$. Let's calculate $$$dp[i][l]$$$: the index we'll end up at if we keep replacing $$$l$$$ with $$$go_l$$$ $$$2^i$$$ times. Clearly, $$$dp[i][l]=dp[i-1][dp[i-1][l]]$$$ since $$$2^{i-1}+2^{i-1}=2^i$$$. Now, to calculate how many steps it takes from index $$$l$$$ to index $$$r$$$, let's iterate over the numbers from $$$log(n)$$$ to $$$0$$$. Let the current be $$$i$$$. If $$$dp[i][l]$$$ is less than or equal to $$$r$$$, we can jump $$$2^i$$$ steps at once, so we'll make $$$l$$$ equal to $$$dp[i][l]$$$ and add $$$2^i$$$ to the answer. At the end, we'll make one more jump.
Code link: https://pastebin.com/Ng314Xc8
1516E - Baby Ehab Plays with Permutations
Let's think about the problem backwards. Let's try to count the number of permutations which need exactly $$$j$$$ swaps to be sorted. To do this, I first need to refresh your mind (or maybe introduce you) to a greedy algorithm that does the minimum number of swaps to sort a permutation. Look at the last mismatch in the permutation, let it be at index $$$i$$$ and $$$p_i=v$$$. We'll look at where $$$v$$$ is at in the permutation, and swap index $$$i$$$ with that index so that $$$v$$$ is in the correct position. Basically, we look at the last mismatch and correct it immediately. We can build a slow $$$dp$$$ on this greedy algorithm: let $$$dp[n][j]$$$ denote the number of permutations of length $$$n$$$ which need $$$j$$$ swaps to be sorted. If element $$$n$$$ is in position $$$n$$$, we can just ignore it and focus on the first $$$n-1$$$ elements, so that moves us to $$$dp[n-1][j]$$$. If it isn't, then we'll swap the element at position $$$n$$$ with wherever $$$n$$$ is at so that $$$n$$$ becomes in the right position, by the greedy algorithm. There are $$$n-1$$$ positions index $$$n$$$ can be at, and after the swap, you can have an arbitrary permutation of length $$$n-1$$$ that needs to be sorted; that gives us $$$n-1$$$ ways to go to $$$dp[n-1][j-1]$$$. Combining, we get that $$$dp[n][j]=dp[n-1][j]+(n-1)*dp[n-1][j-1]$$$.
Next, notice that you don't have to do the minimum number of swaps in the original problem. You can swap $$$2$$$ indices and swap them back. Also, it's well-known that you can either get to a permutation with an even number of swaps or an odd number, but never both (see this problem.) So now, after you calculate your $$$dp$$$, the number of permutations you can get to after $$$j$$$ swaps is $$$dp[n][j]+dp[n][j-2]+dp[n][j-4]+...$$$. Now, let's solve for $$$n \le 10^9$$$.
Sane solution
Notice that after $$$k$$$ swaps, only $$$2k$$$ indices can move from their place, which is pretty small. That gives you a pretty intuitive idea: let's fix a length $$$i$$$ and then a subset of length $$$i$$$ that will move around. The number of ways to pick this subset is $$$\binom{n}{i}$$$, and the number of ways to permute it so that we need $$$j$$$ swaps is $$$dp[i][j]$$$. So we should just multiply them together and sum up, right? Wrong. The problem is that double counting will happen. For example, look at the sorted permutation. This way, you count it for every single subset when $$$j=0$$$, but you should only count it once. A really nice solution is: force every element in your subset to move from its position. How does this solve the double counting? Suppose $$$2$$$ different subsets give you the same permutation; then, there must be an index in one and not in the other. But how can they give you the same permutation if that index moves in one and doesn't move in the other?
So to mend our solution, we need to create $$$newdp[n][j]$$$ denoting the number of permutations of length $$$n$$$ which need $$$j$$$ swaps to be sorted, and every single element moves from its position (there's no $$$p_i=i$$$.) How do we calculate it? One way is to do inclusion-exclusion on the $$$dp$$$ we already have! Suppose I start with all permutations which need $$$j$$$ swaps. Then, I fix one index, and I try to subtract the number of permutations which need $$$j$$$ swaps to be sorted after that index is fixed. There are $$$n$$$ ways to choose the index, and $$$dp[n-1][j]$$$ permutations, so we subtract $$$n*dp[n-1][j]$$$. But now permutations with $$$2$$$ fixed points are excluded twice, so we'll include them, and so on and so forth. In general, we'll fix $$$f$$$ indices in the permutation. There are $$$\binom{n}{f}$$$ ways to pick them, and then there are $$$dp[n-f][j]$$$ ways to pick the rest so that we need $$$j$$$ swaps. Hence: $$$newdp[n][j]=\sum\limits_{f=0}^{n} (-1)^f*\binom{n}{f}*dp[n-f][j]$$$. Phew!
If you have no idea what the hell I was talking about in the inclusion-exclusion part, try this problem first.
Code link: https://pastebin.com/3CzuGvtw
Crazy solution
Let $$$[l;r]$$$ denote the set of the integers between $$$l$$$ and $$$r$$$ (inclusive.)
Let's try to calculate $$$dp[2n]$$$ from $$$dp[n]$$$. To do that, we need to understand our $$$dp$$$ a bit further. Recall that $$$dp[n][j]=dp[n-1][j]+(n-1)*dp[n-1][j-1]$$$. Let's think about what happens as you go down the recurrence. When you're at index $$$n$$$, either you skip it and move to $$$n-1$$$, or you multiply by $$$n-1$$$. But you do that exactly $$$j$$$ times, since $$$j$$$ decreases every time you do it. So, this $$$dp$$$ basically iterates over every subset of $$$[0;n-1]$$$ of size $$$j$$$, takes its product, and sums up!
Now, let's use this new understanding to try and calculate $$$dp[2n]$$$ from $$$dp[n]$$$. suppose I pick a subset of $$$[0;2n-1]$$$. Then, a part of it will be in $$$[0;n-1]$$$ and a part will be in $$$[n;2n-1]$$$. I'll call the first part small and the second part big. So, to account for every subset of length $$$j$$$, take every subset of length $$$j_2$$$ of the big elements, multiply it by a subset of length $$$j-j_2$$$ of the small elements, and sum up. This is just normal polynomial multiplication!
Let $$$big[n][j]$$$ denote the sum of the products of the subsets of length $$$j$$$ of the big elements. That is:
Then, the polynomial multiplication between $$$dp[n]$$$ and $$$big[n]$$$ gives $$$dp[2n]$$$! How do we calculate $$$big$$$ though?
Notice that every big element is a small element plus $$$n$$$. So we can instead pick a subset of the small elements and add $$$n$$$ to each element in it. This transforms the formula to:
Let's expand this summand. What will every term in the expansion look like? Well, it will be a subset of length $$$l$$$ from our subset of length $$$j$$$, multiplied by $$$n^{j-l}$$$. Now, let's think about this backwards. Instead of picking a subset of length $$$j$$$ and then picking a subset of length $$$l$$$ from it, let's pick the subset of length $$$l$$$ first, and then see the number of ways to expand it into a subset of length $$$j$$$. Well, there are $$$n-l$$$ elements left, and you should pick $$$j-l$$$ elements from them, so there are $$$\binom{n-l}{j-l}$$$ ways to expand. That gives use:
But the interior sum is just $$$dp[l]$$$! Hurray! So we can finally calculate $$$big[n][j]$$$ to be:
And then polynomial multiplication with $$$dp[n]$$$ itself would give $$$dp[2n]$$$. Since you can move to $$$dp[n+1]$$$ and to $$$dp[2n]$$$, you can reach any $$$n$$$ you want in $$$O(log(n))$$$ iterations using its binary representation.
Code link: https://pastebin.com/yWgs3Ji6
Bonus task-ish: the above solutions can be made to work with $$$k \le 2000$$$ with a bit of ugly implementation, but I don't know how to solve the problem with $$$k \le 10^5$$$. Can anyone do it? The sane solution seems far off, and I don't know if it's possible to do the convolution from $$$dp$$$ to $$$big$$$ quickly in the crazy one.









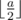 ,
, 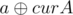 and
and 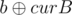 have all bits from the most significant to the
have all bits from the most significant to the 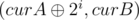 and
and 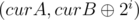 .
.  and
and  can only differ in the
can only differ in the 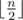 .
.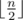 . Second, the found vertex cover is also at most
. Second, the found vertex cover is also at most 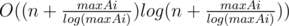 because the
because the 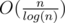 .
.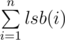 , which means that node
, which means that node 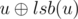 for all
for all 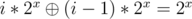 because
because 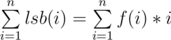 .
. 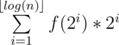 . Basically, the first number
. Basically, the first number 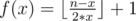 for
for 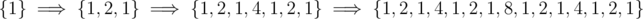
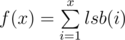 . Let
. Let 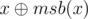 which is
which is 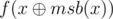 . Therefore,
. Therefore, 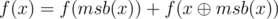 . The first part can be calculated with the help of our
. The first part can be calculated with the help of our  to the set for all
to the set for all  must be in the set. To see that, let
must be in the set. To see that, let 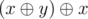 must be in the set. This is equivalent to
must be in the set. This is equivalent to 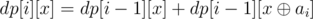 . The intuition behind it is exactly the same as the intuition behind the set construction. Let's prove that
. The intuition behind it is exactly the same as the intuition behind the set construction. Let's prove that 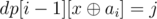 which makes
which makes 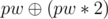 , Otherwise you can add
, Otherwise you can add 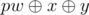 , We handled the case
, We handled the case 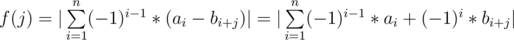
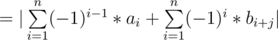
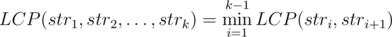 , That could make us transform the
, That could make us transform the 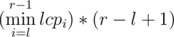 , If we have a histogram where the
, If we have a histogram where the 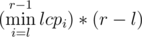 , That's close to our formula not the same but it's not a problem (You'll see how to fix it later), so to get rid of finding the
, That's close to our formula not the same but it's not a problem (You'll see how to fix it later), so to get rid of finding the  big columns (Where
big columns (Where 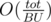 , The stack way will get us the maximum width
, The stack way will get us the maximum width 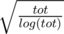 (Reason in
(Reason in 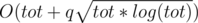
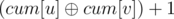 , Now to answer suspended relations, Find the relation between the 2 words and check if it's the same as the input relation, Then answer the queries.
, Now to answer suspended relations, Find the relation between the 2 words and check if it's the same as the input relation, Then answer the queries.