1088A - Ehab and another construction problem
Well, the constraints allow a brute-force solution, but here's an O(1) solution:
If x = 1, there's no solution. Otherwise, just print x - x%2 and 2.
Code link: https://pastebin.com/LXvuX8Ez
Time complexity: O(1).
1088B - Ehab and subtraction
Let s be the set of numbers in input (sorted and distinct). In the ith step, si is subtracted from all bigger or equal elements, and all smaller elements are 0. Thus, the answer in the ith step is si - si - 1 (s0 = 0).
Code link: https://pastebin.com/bpz1YxBe
Time complexity: O(nlog(n)).
1088C - Ehab and a 2-operation task
The editorial uses 0-indexing.
Both solutions make ai = i.
First solution, n adds and 1 mod
First, let's make ai = x * n + i (for some x). Then, let's mod the whole array with n (making ai = i). If the "add update" changed one index, we can just add i + n - ai%n to index i. The problem is, if we make ai = x * n + i, then update an index j > i, ai will be ruined. Just start from the back of the array!
Code link: https://pastebin.com/dBfhNBL8
Second solution, 1 add and n mods
Note: for any a, b, if b > a, a%b = a. Additionally, if a ≥ b > 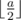 , a%b = a - b.
, a%b = a - b.
Let's add 5·105 to the whole array, loop over ai (in order), and mod prefix i with ai - i. Why does this work? Notice that ai%(ai - i) = ai - (ai - i) = i (the second note). Also, ai won't be changed afterwards (the first note).
Code link: https://pastebin.com/L6suPC1f
Time complexity: O(n).
1088D - Ehab and another another xor problem
This problem is particularly hard to explain :/ I recommend the simulation.
Let's build a and b bit by bit from the most significant to the least significant (assume they're stored in curA and curB). Then, at the ith step, 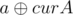 and
and 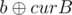 have all bits from the most significant to the (i + 1)th set to 0. Notice that whether x is greater or less than y is judged by the most significant bit in which they differ (the one that has 1 is bigger). Let's query with
have all bits from the most significant to the (i + 1)th set to 0. Notice that whether x is greater or less than y is judged by the most significant bit in which they differ (the one that has 1 is bigger). Let's query with 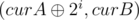 and
and 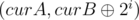 .
.  and
and  can only differ in the ith bit (or a bit less significant). Now, if the results of the queries are different, a and b have the same value in this bit, and this value can be determined by the answer of respective queries (1 if the second query's answer is 1, 0 otherwise). If the queries give the same result, a and b must differ in this bit. How to know which of them has a 1 and which has a 0? We know that the greater between them (after setting the processed bits to 0) has a 1 and the other has a 0. The trick is to keep track of the greater between them. Before all queries, we send (0, 0) to know the greater. Every time they differ in a bit, the greater may change. It'll simply change to the answer of the 2 queries we sent! In other words, we know when we sent the queries that after making a and b equal in this bit, some other bit became the most significant bit in which they differ. Also, we know who has a 1 in this bit (the greater in this query). Thus, we'll keep the answer of this query for the future, so when this bit comes, we don't need additional queries.
can only differ in the ith bit (or a bit less significant). Now, if the results of the queries are different, a and b have the same value in this bit, and this value can be determined by the answer of respective queries (1 if the second query's answer is 1, 0 otherwise). If the queries give the same result, a and b must differ in this bit. How to know which of them has a 1 and which has a 0? We know that the greater between them (after setting the processed bits to 0) has a 1 and the other has a 0. The trick is to keep track of the greater between them. Before all queries, we send (0, 0) to know the greater. Every time they differ in a bit, the greater may change. It'll simply change to the answer of the 2 queries we sent! In other words, we know when we sent the queries that after making a and b equal in this bit, some other bit became the most significant bit in which they differ. Also, we know who has a 1 in this bit (the greater in this query). Thus, we'll keep the answer of this query for the future, so when this bit comes, we don't need additional queries.
Code link: https://pastebin.com/b9zgKuJ6
Time complexity: O(log(n)).
1088E - Ehab and a component choosing problem
Assume you already chose the components. Let the sum of nodes in the ith component be bi. Then, the expression in the problem is equivalent to average(b1, b2, ..., bk). Assume we only bother about the fraction maximization problem and don't care about k. Then, it'll always be better to choose the component with the maximum bi and throw away the rest! This is because of the famous inequality:
max(b1, b2, ..., bk) ≥ average(b1, b2, ..., bk) and the equality only occurs if all bi are equal!
This means that the maximum value of the fraction is simply the maximum sum of a sub-component in the tree. To calculate it, let's root the tree at node 1, and calculate dp[node], the maximum sum of a sub-component that contains node. Now, I'll put the code, and explain it after.
void dfs(int node,int p,bool f)
{
dp[node]=a[node];
for (int u:v[node])
{
if (u!=p)
{
dfs(u,node,f);
dp[node]+=max(dp[u],0LL);
}
}
if (f)
ans=max(ans,dp[node]);
else if (dp[node]==ans)
{
dp[node]=0;
k++;
}
}
ans denotes the maximum sub-component sum.
First, we call dfs(1, 0, 1). We calculate the dp of all the children of node. For every child u, we extend the component of node with the component of u if dp[u] > 0, and do nothing otherwise. Now, we solved the first half of our problem, but what about maximizing k? Notice that all components you choose must have a sum of weights equal to ans (because the equality occurs if and only if all bi are equal). You just want to maximize their count. Let's calculate our dp again. Assume dp[node] = ans. We have 2 choices: either mark the node and its component as a component in the answer (but then other nodes won't be able to use them because the components can't overlap), or wait and extend the component. The idea is that there's no reason to wait. If we extend the component with some nodes, they won't change the sum, and they may even have another sub-component with maximal sum that we're merging to our component and wasting it! Thus, we'll always go with the first choice, making dp[node] = 0 so that its parent can't use it, and increasing k :D
Code link: https://pastebin.com/8pCrTfuP
Time complexity: O(n).
1088F - Ehab and a weird weight formula
First, let's reduce the problem to ordinary MST. We know that each edge {u, v} adds ⌈log2(dist(u, v))⌉·min(au, av) to w. In fact, it also adds 1 to degu and degv. Thus, the problem is ordinary MST on a complete graph where each edge {u, v} has weight (⌈log2(dist(u, v))⌉ + 1)·min(au, av) + max(au, av)!
Let the node with the minimum weight be m. Let's root the tree at it.
Lemma: for every node u and a child v, av > au. In simpler words, the weight increase as we go down the tree.
Proof: the proof is by contradiction. Assume av ≤ au. Then, the condition in the problem (that every node has an adjacent node with less weight) isn't satisfied yet for v. Therefore, v must have a child k such that ak < av. However, the condition isn't satisfied for k, so k needs another child and the child needs another child etc. (the tree will be infinite) which is clearly a contradiction.
From that, we know that the weights decrease as we go up the tree and increase as we go down.
Back to the MST problem. From Kruskal's algorithm, we know that the minimal edge incident to every node will be added to the MST (because the edges are sorted by weight). Let's analyze the minimal edge incident to every node u. Let its other end be v. Except for node m, v will be an ancestor of u. Why? Assume we fix the distance part and just want to minimize av. We'll keep going up the tree (it's never optimal to go down, since the weights will increase) until we reach the desired distance. Now, since the minimal edge incident to every node will be added to the MST (by Kruskal's algorithm), and they're distinct (because, otherwise, you're saying that u is an ancestor of v and v is an ancestor of u), THEY ARE THE MST. Now, the problem just reduces to finding the minimal edge incident to every node and summing them up (except for m). To do that, we'll fix the ⌈log2(dist(u, v))⌉ (let it be k), and get the 2kth ancestor with the well-known sparse-table (binary lifting).
Code link: https://pastebin.com/vzJqh8si
Time complexity: O(nlog(n)).










Thank you for the fast editorial :)
How would we be able to find the first problem logic manh!!!
for the first problem you can also print n and n.
Why not just n and n for problem A??
So fast editorial ! Thank you.
In F statement, English was bad
Why 5.105 specifically? Won't 105 be enough?
It doesn't have to be 5·105. Actually, any number starting from 3999 should work.
My solutions works with just reading n:
https://codeforces.com/contest/1088/submission/46624854
Wow!!! Excellent solution.
awesome !
Brilliant thinking!!
jv
Thanks! I also tried to solve this by making all elements equal to 10e6 but then I didnt know how to make elements before the last element to be an increasing series of numbers and your solution helps me alot. Thanks again!
Can someone explain why 2nd given output for F is 40? I tried using the optimal tree given and my output comes out to 44..
For Problem A, for x > 1, a = x and b = x will always be valid.
I find this explanation for C much easier to understand than the second one given in the editorial.
For C, I'm unsure why my submission fails at pretest 2. I traced out the moves and the array should be strictly increasing.
I think I am overlooking something obvious. Can someone take a quick glance?
initial array is
7 6 3then you do operation
2 1 32 1 32 1 35 4 6its not strictly increasing
Can someone explain me D?
In D we will query in such a fashion that we will get bits from left to right(MSB to LSB) for both numbers. Firstly we will know which number is greater by querying c = 0, d = 0 and store which is bigger in a variable larger. We are also going to maintain two variables a1 = 0 and b1 = 0 which will going be our final answer. These variables will store bits after every iteration.
Now from leftmost bit till rightmost bit we will do 2 queries for i bit c = a1(1«i), d = b1 and c = a1, d = b1(1«i). Four cases can be made:
1. When ith bit of only a is 1
2. When ith bit of only b is 1
3. When ith bit of both a and b is 1
4. When ith bit of both a and b is 0
When it is first case, the result of first and second query depends on how upcoming bits are set. Same will happen when it is second case. eq. let a = 10110, b = 10011. Till 2nd bit(from left) a1 = 10000, b1 = 10000. When we give first query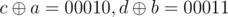 and when we give second query
and when we give second query 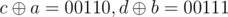 . Hence, we get same result. We set bit of a1 or b1 depending on variable larger and update larger.
. Hence, we get same result. We set bit of a1 or b1 depending on variable larger and update larger.
When it is third or fourth case, the result of first and second query will be different. Think about it. Due to query first number gains or loses its ith bit in first query and same is with second number in second query. eg. let a = 10110, b = 10011. Till 3rd bit a1 = 10100, b1 = 10000. When we give first query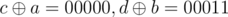 and when we give second query
and when we give second query  . Hence, we get different result. We will set bit of a1 or b1 when first query gives - 1.
. Hence, we get different result. We will set bit of a1 or b1 when first query gives - 1.
I hope I made it clear.
My Code
I'm trying to re-do problem F but I'm confused. Maybe I'm missing something?
Q1. We are given a tree, but we are also asked to construct a tree, then what's the input tree for?
Q2. I think I don't understand why example 2 gives 40...hopefully if question Q1 is clear Q2 is clear as well.
Thanks
I think i understand now after looking at the solution...
problem statement could've been clearer
how in solution of problem b array is taken sorted when in second test case it in the unsorted array as input?
The input array is sorted first and then the editorial comes into play, it can be proved that the sorted form of input array and the original unsorted input array would give the same answer.
How would one approach problem C if we were asked to determine the minimum number of steps to make the array strictly increasing??
Anyone out there??
Hey 1st problem is quite easily done in another way
if x is 1 print -1.
else print x , x
(as x%x==0 & x*x>x & x/x < x for all x>1)
In problem F, while we're minimizing the weight to parent, why are we skipping the internal non-power-of-two-th parents?
Because when we fix k, we want to go up as much as possible (to decrease the weight), so it's sufficient to only try the 2kth ancestor.
An alternate way to approach C. (Using 1 indexing)
1st take mod of all elements by 1 and make the array 0.
Then add 100000 to all the indices in the array.
Next starting from the (n-1)th index to the 1st index take mod at the ith index with (100000-(n-i)).
Solution Code — https://codeforces.com/contest/1088/submission/46622025
How would one approach problem C if we were asked to determine the minimum number of steps to make the array strictly increasing?? Anyone out there??
Python2.x 5 lines implementation of solution for B:
read more here: https://codeforces.com/blog/entry/60059
My solution for F using centroid decomposition, barely squeezed into the time limit!
solution for F using centroid decomposition, barely squeezed into the time limit!
One technical thing. In F you don't need binary lifting. You can just keep the stack with the path, iterate through all the groups (values which have the same ceiling of log) and take the last one on that path.
Code
Can someone please have a look at my code for problem D? 53433106
Apparently it fails for 10,5 but works fine locally.
thanks
Hi mohammedehab2002, Thanks for the comprehensive editorial, really enjoyed reading about Problem C!
I was reading the solution for Problem D, and was wondering if you can explain both the parts —
wait and extend the componentandmark the node and its component as a component in the answer, in this line -Thanks :)
in problem c
if i make element[n-1] in the array the biggest element using operation (1)
and element[n-2]=element[n-1]-1
and element[n-3]=element[n-1]-2 ,etc.. just using operation (1)
why this not working? my code