Introduction
This is a tutorial/exploration of problems that can be solved using the "DFS tree" of a graph.
For a way too long time, I didn't really understand how and why the classical algorithm for finding bridges works. It felt like many tutorials didn't really explain how it works, kind of just mentioned it in passing and quickly just moved on to implementation. The day someone explained what the DFS tree is, I finally understood it properly. Before, it took me ages to implement bridge-finding properly, and I always had to look up some detail. Now I can implement it at typing speed.
But more importantly, I began to see how the same techniques can be used to solve graph problems that have more or less nothing to do with bridges. The thing is, when you have a black box, you can only ever use it as a black box. But if you have a box that you understand well, you can take it into pieces, repurpose the pieces for completely different things, all without getting lost.
In my opinion, the DFS tree one of the most useful techniques for solving structural problems about graphs that I know of. Also, sometimes there are questionable greedy algorithms whose correctness becomes obvious once you think about the DFS tree. $$$~$$$
The DFS tree
Consider an undirected connected graph $$$G$$$. Let's run a depth-first traversal of the graph. It can be implemented by a recursive function, perhaps something like this:
1 function visit(u):
2 mark u as visited
3 for each vertex v among the neighbours of u:
4 if v is not visited:
5 mark the edge uv
6 call visit(v)
Here is an animation of what calling visit(1) looks like.
Let's look at the edges that were marked in line 5. They form a spanning tree of $$$G$$$, rooted at the vertex 1. We'll call these edges span-edges; all other edges are called back-edges.
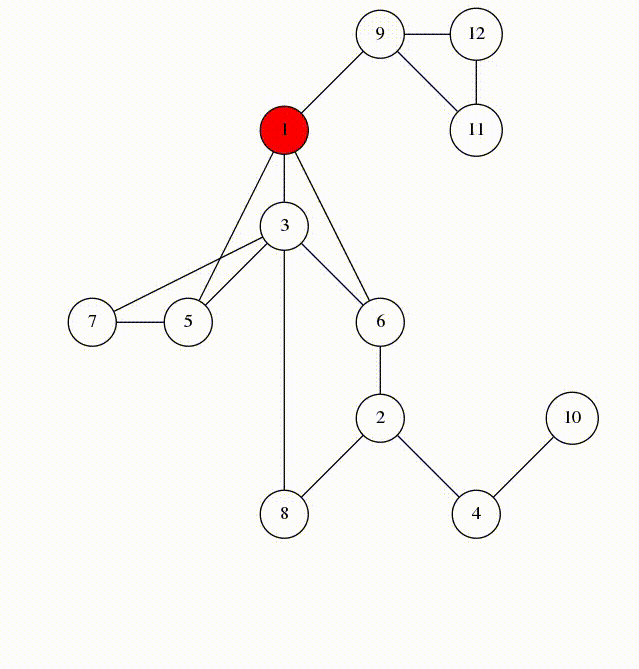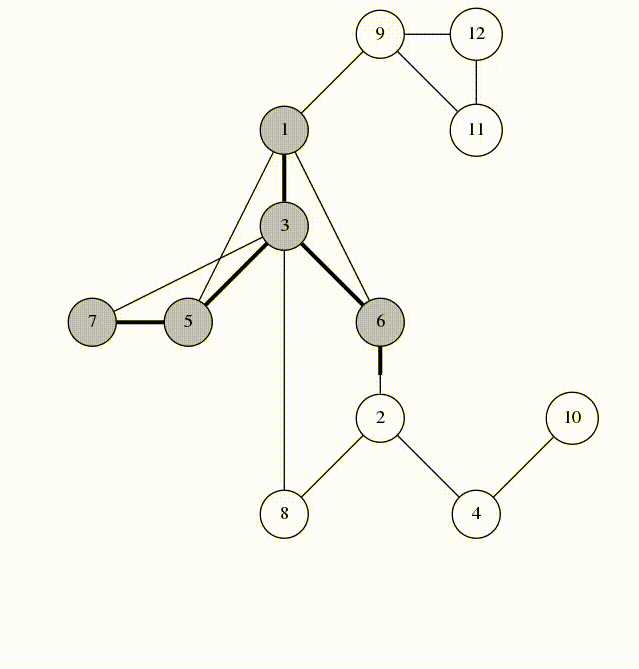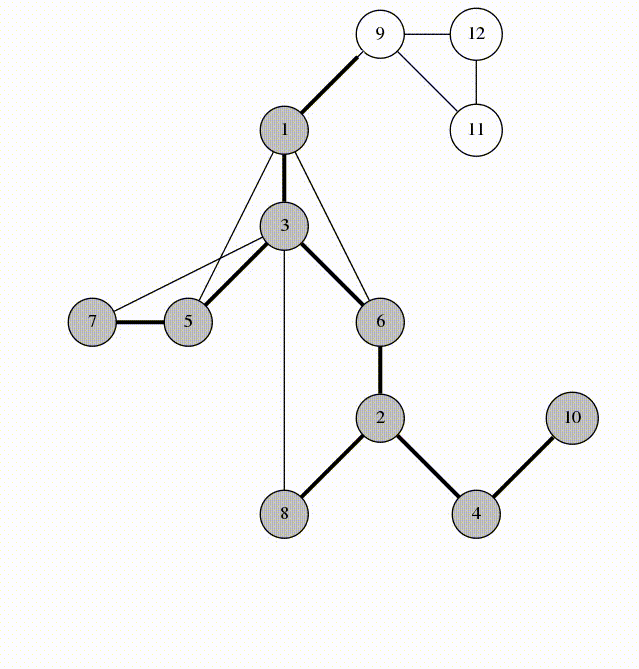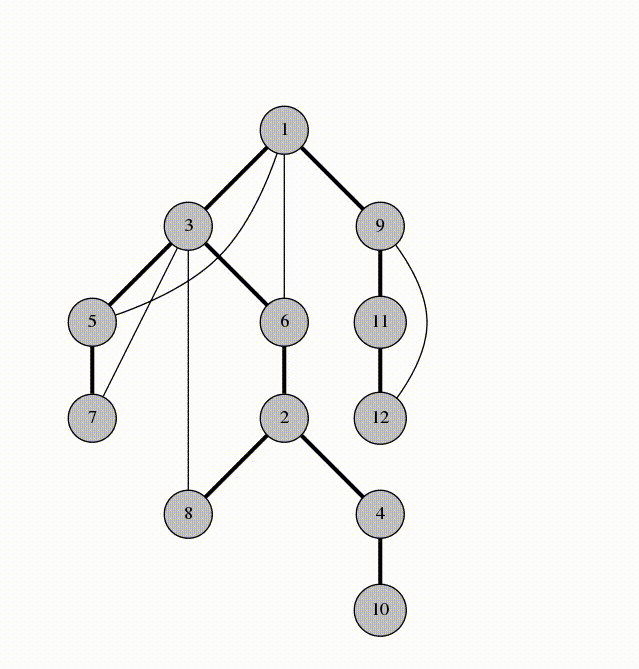
This is the DFS tree of our graph:
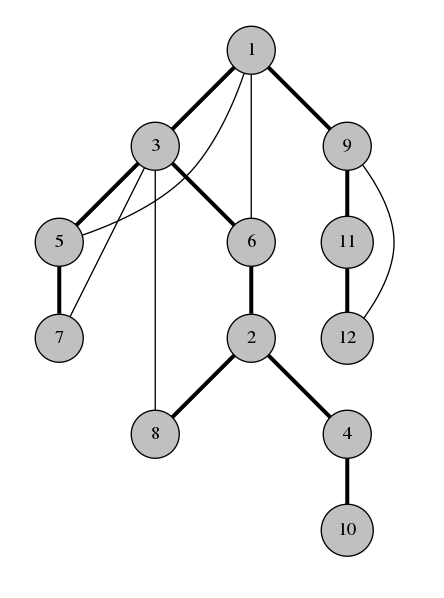
Observation 1. The back-edges of the graph all connect a vertex with its descendant in the spanning tree. This is why DFS tree is so useful.
For example in the graph above, vertices 4 and 8 couldn't possibly have a back-edge connecting them because neither of them is an ancestor of the other. If there was an edge between 4 and 8, the traversal would have gone to 8 from 4 instead of going back to 2.
This is the most important observation about about the DFS tree. The DFS tree is so useful because it simplifies the structure of a graph. Instead of having to worry about all kinds of edges, we only need to care about a tree and some additional ancestor-descendant edges. This structure is so much easier to think and write algorithms about.
Finding bridges (or articulation points)
The DFS tree and observation 1 are the core of Tarjan's bridge-finding algorithm. Typical tutorials about finding bridges only mention the DFS tree in passing and start by defining weird arrays like $$$\mathrm{dfs}[u]$$$ and $$$\mathrm{low}[u]$$$: forget all that. These are implementation details, and in my opinion this isn't even the most intuitive way to implement finding bridges. In bridge-finding, $$$\mathrm{dfs}[u]$$$ is simply an obfuscated way to check whether one vertex is an ancestor of another in the DFS tree. Meanwhile it is even kind of hard to clearly explain what $$$\mathrm{low}[u]$$$ is supposed to represent.
Here's how to find bridges in an undirected connected graph $$$G$$$. Consider the DFS tree of $$$G$$$.
Observation 2. A span-edge $$$uv$$$ is a bridge if and only if there exists no back-edge that connects a descendant of $$$uv$$$ with an ancestor of $$$uv$$$. In other words, a span-edge $$$uv$$$ is a bridge if and only if there is no back-edge that "passes over" $$$uv$$$.
For example, in the DFS tree above, the edge between 6 and 2 isn't a bridge, because even if we remove it, the back-edge between 3 and 8 holds the graph together. On the other hand, the edge between 2 and 4 is a bridge, because there is no back-edge passing over it to hold the graph together if $$$2-4$$$ is removed.
Observation 3. A back-edge is never a bridge.
This gives rise to the classical bridge-finding algorithm. Given a graph $$$G$$$:
- find the DFS tree of the graph;
- for each span-edge $$$uv$$$, find out if there is a back-edge "passing over" $$$uv$$$, if there isn't, you have a bridge.
Because of the simple structure of the DFS tree, step 2 is easy to do. For example, you can use the typical $$$\mathrm{low}[u]$$$ method. Or, for example, you can use some kind of prefix sums, which is what I prefer. I define $$$\mathrm{dp}[u]$$$ as the number of back-edges passing over the edge between $$$u$$$ and its parent. Then,
The edge between $$$u$$$ and its parent is a bridge if and only if $$$\mathrm{dp}[u] = 0$$$.
Directing edges to form a strongly connected graph
Consider the following problem. Unfortunately I don't know if you can submit solutions somewhere. This is 118E - Bertown roads.
Problem 1. You are given an undirected connected graph $$$G$$$. Direct all of its edges so that the resulting digraph is strongly connected, or declare that this is impossible.
I know of a solution without using the ideas of DFS tree in linear time, but it is quite annoying and I would never want to implement this. Meanwhile, a DFS tree solution is very easy to implement in only a few lines of code.
Observation 4. If $$$G$$$ contains bridges, this is impossible.
So from now on, suppose that the graph doesn't have bridges. Let's look at its DFS tree. Direct all span-edges downwards and all back-edges upwards.
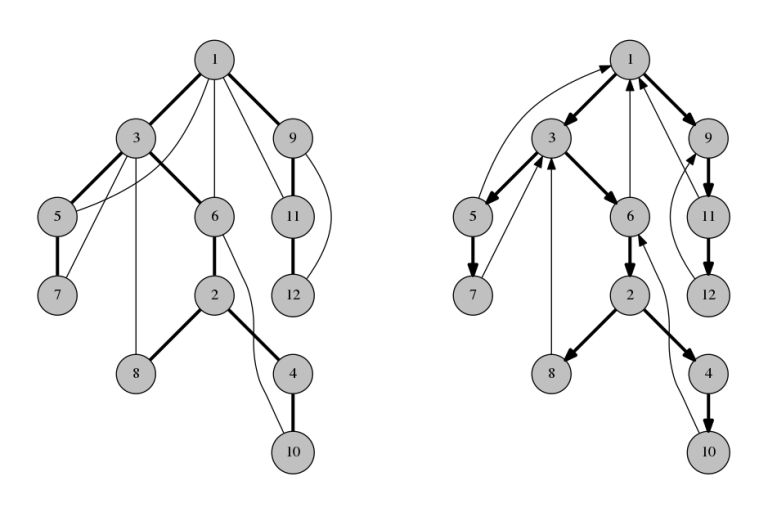
Observation 5. There is a path from the root to each vertex.
Observation 6. There is a path from each vertex to the root.
Therefore, the graph is now strongly connected! This solution can be implemented without an explicit reference to the DFS tree, but it is a very good example of proving the correctness using DFS tree.
Implementing cacti
Sometimes the DFS tree is just a way to represent a graph that makes implementation of certain things convenient. Like an adjacency list but "next level". This section is purely an implementation trick.
A cactus is a graph where every edge (or sometimes, vertex) belongs to at most one simple cycle. The first case is called an edge cactus, the second case is a vertex cactus. Cacti have a simpler structure than general graphs, as such it is easier to solve problems on them than on general graphs. But only on paper: cacti and cactus algorithms can be very annoying to implement if you don't think about what you are doing.
In the DFS tree of a cactus, for any span-edge, at most one back-edge passes over it. This puts cycles to an one-to-one correspondence with simple cycles:
- each back-edge forms a simple cycle together with the span-edges it passes over;
- there are no other simple cycles.
This captures most properties of cacti. Often, it is easy to implement cactus algorithms using this representation.
For example, consider this problem:
Problem 2. You are given a connected vertex cactus with $$$N$$$ vertices. Answer queries of the form "how many distinct simple paths exist from vertex $$$p$$$ to vertex $$$q$$$?".
This is named appropriately: 231E - Cactus. The official tutorial has a solution like this:
- "squeeze" every cycle to a single vertex, and paint these vertices black;
- root the tree;
- for each vertex $$$u$$$, calculate the number of black vertices on the path from the root to $$$u$$$; denote this $$$\mathrm{cnt}[u]$$$.
- the answer to query $$$(p, q)$$$ is either $$$2^{\mathrm{cnt}[p] + \mathrm{cnt}[q] - 2 \mathrm{cnt}[\mathrm{lca}(p, q)]}$$$ or $$$2^{\mathrm{cnt}[p] + \mathrm{cnt}[q] - 2 \mathrm{cnt}[\mathrm{lca}(p, q)] + 1}$$$ depending on the color of $$$\mathrm{lca}(p, q)$$$.
It isn't very hard to understand why this works. The more interesting part is implementation.
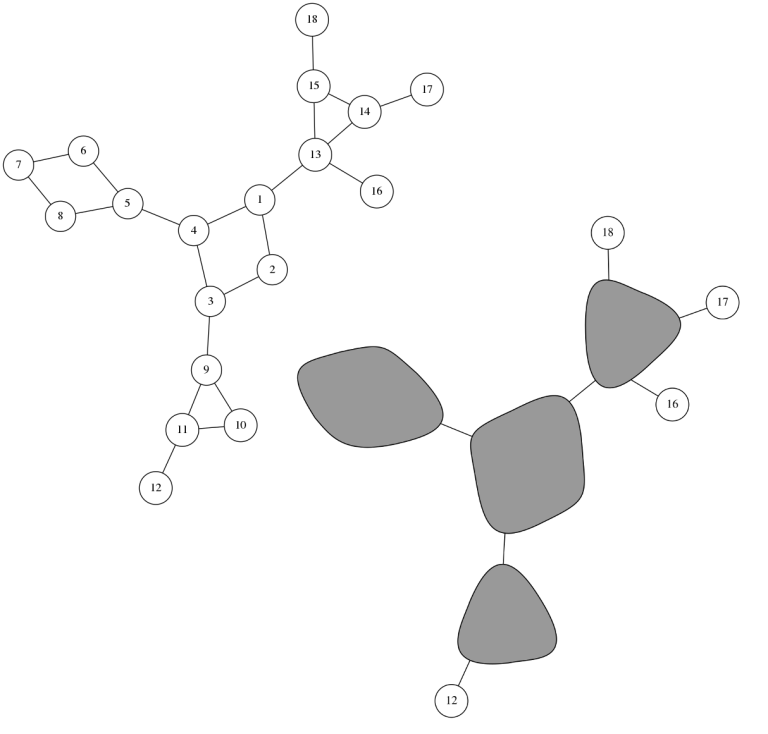
- "squeeze" every cycle to a single vertex, and paint these vertices black;
Great. How?
After some time, most people will probably find some way to implement this. But here is a simple way using the DFS tree:
- give each back-edge an unique index starting from $$$N + 1$$$;
- for each vertex $$$u$$$, calculate the index of the back-edge $$$u$$$ is under; call that $$$\mathrm{cycleId}[u]$$$; if $$$u$$$ isn't in a cycle then $$$\mathrm{cycleId}[u] = u$$$;
- form a new adjacency list where for each $$$u$$$, each instance of $$$u$$$ is replaced by $$$\mathrm{cycleId}[u]$$$.
Step 2 can be done like this, for example:
1 function visit(u):
2 for each vertex v among the children of u:
3 visit(v)
4
5 if there is a back-edge going up from u:
6 cycleId[u] = the index of that back-edge
7 else:
8 cycleId[u] = u
9 for each vertex v among the children of u:
10 if cycleId[v] != v and there is no back-edge going down from v:
11 cycleId[u] = cycleId[v]
Removing edges to form a bipartite graph
Problem 3. Consider an undirected graph. Find all the edges whose removal will produce a bipartite graph.
This is 19E - Fairy. There is no official tutorial, but an unofficial tutorial mentions using complicated data structures like Link/cut tree. Using DFS tree, we can solve the problem without any advanced data structures.
In the original problem, the graph need not be connected. However, observe that:
- if the graph has no non-bipartite connected components, then removing any edge will produce a bipartite graph;
- if the graph has multiple non-bipartite connected components, then it is not possible to make the graph bipartite.
Thus, the only interesting case is when we have exactly one non-bipartite connected component. Obviously the edge we remove must also come from that component, so we can just pretend that this is the only component. From now on, we assume that we have a non-bipartite, connected graph.
Let's consider the DFS tree of the graph. We can paint the vertices black and white so that each span-edge connects a black vertex and a white vertex. Some back-edges, however, might connect two vertices of the same color. We will call these edges contradictory.
Observation 7. A back-edge $$$uv$$$ is a solution if and only if $$$uv$$$ is the only contradictory edge.
Observation 8. A span-edge $$$uv$$$ is a solution if and only if the set of back-edges passing over $$$uv$$$ is the set of contradictory edges.
Thus, we can solve the problem as such:
- find the DFS tree of the graph and paint it in two colors;
- if there is exactly one contradictory back-edge, add it to the answer;
- use dynamic programming to calculate, for each span-edge, how many contradictory and how many non-contradictory back-edges pass over it;
- if a span-edge has all contradictory and no non-contradictory edges passing over it, add it to the answer.
Directed variant
What happens if we find the DFS tree of a directed graph? Let's run our depth-first traversal again:
1 function visit(u):
2 mark u as visited
3 for each vertex v among the neighbours of u:
4 if v is not visited:
5 mark the edge u->v
6 call visit(v)
To clarify, on line 3 we only mean such vertices $$$v$$$ that there is an edge from $$$u$$$ to $$$v$$$.
It might be the case that this traversal never reaches some vertices. For simplicity, we assume that:
- we started the traversal at vertex 1, i.e. called
visit(1); - it is possible to reach every vertex from the vertex 1.
Let's call the edges marked at step 5 span-edges.
Observation 9. Span-edges form a rooted spanning tree, directed away from the root.
Other edges fall in two categories:
- edges that connect an ancestor with a descendant: back-edges;
- edges that don't: cross-edges.
It's possible to further divide the back-edges into up-edges and down-edges based on their direction.
Observation 10. Cross-edges are always directed from the vertex that was explored later, to the vertex that was explored earlier.
The directed variant of DFS tree is used to construct the dominator tree of a directed graph, but that is a beast on a whole another level that warrants its own tutorial.
Problems for practice
Solved in this tutorial:
Others:
- 858F - Wizard's Tour
- 412D - Giving Awards
- 101612G - Grand Test
- any task where you have to find a block-cut tree
If you know any other tasks that can be solved like this, share in the comment section! I might add them here, too.










Very nice tutorial :)
I know these 3 problems which are related to the post:
1391E Pairs of Pairs
Adding another
I'm putting this in my great-articles-to-recommend file. Great blog, make more :)
How did you make the animation?
I would love to see your list. Do you maintain it on your github page ?
https://github.com/Errichto/youtube/wiki/Learning-resources
The list is small right now but you will find more useful things in the menu on the right, e.g. "How to practice?".
Thank you!
For animation, I used this GraphViz library for Python. Then I just made a script to draw the animation frame by frame: 1, 2 (the first script contains general methods to draw graphs and the second one draws DFS tree specifically). Finally I used some command-line tool to join the frames into an animation.
Oh and also, the "partially bold edges" are actually two edges stacked on top of each other: a bolder black and white edge in the bottom and a thinner black edge on top.
(uses similar concept) https://www.codechef.com/IPC15P3B/problems/SROADS
Really cool graph problem that uses some ideas related to the post (I will not say about the subject because it might facilitate the probem, and it deserve your thinking time, in my opinion :D )
Link -> https://codeforces.com/problemset/problem/1000/E
Very relevant. This question felt so easy using the dfs tree concept.
So, does your bridge finding algorithm use only one additional array? In that case it should be faster than the common one, did you measure that?
Does it work when parallel edges are allowed?
It would be nice to see the actual code to get the answers.
Well no, because you still need a way to track whether a back-edge goes "up" or "down". Here is an implementation (and here is the classical one for reference). You can notice that the array
lvl[u]here kind of acts likedfs[u]in the common implementation, butdp[u]andlow[u]work quite differently.I don't think it's much faster or slower than the common one. Indeed, on a practice problem I submitted to, "classical" got 200ms while mine took 280ms. But there are a lot of factors at play here and I don't really have much experience in optimizing the constant.
Really, the reason I put this bridge-finding variant here was:
low[u]is not a "fundamental" concept in finding bridges;Parallel edges work fine.
On line 28 in your implementation why are we subtracting one from the root node which has no parent back-edge.
It doesn't really matter. Later, we only increment the bridge-counter if the given vertex isn't the root anyway (because the root has
lvl[vertex] = 1).If you think about it, you'll find that the value of
dp[root]is never used for anything ever, so it doesn't matter so much what its value is.I feel like that line23 in your implementation is unnecessary because all the back-edges are going upwards. If an edge u->v is going downwards, u must be in the subtree of v, which is a contradiction. Am I right? EDIT: I am wrong.
Which implementation, there are two in my comment?
Never mind, I found where I'm wrong. Sorry for bothering
title truly describes me year ago
It would be great if you could explain why the following works?
dp[u]=(# of back-edges going up from u)−(# of back-edges going down from u)+∑dp[v] v is a child of u.TIA
Sorry for the late response, I just noticed your question. It would be great if Codeforces also sent you a notification if someone responds to your blog. Currently I only get a notification if someone replies to my comment.
Let $$$u$$$ be a vertex and $$$p$$$ be its parent. We want $$$\mathrm{dp}[u]$$$ to be the number of back-edges "passing over" the edge $$$pu$$$.
The edges passing over $$$pu$$$ are:
The first one adds the term $$$(\text{# of back-edges going up from } u)$$$, the second one adds $$$(\sum \mathrm{dp} [v])$$$, and the exception subtracts $$$(\text{# of back-edges going down from } u)$$$.
This is quite an interesting take on the articulation points and bridge concept, your blog-post has been a lifesaver!
Also, would you care to explain what is the logical meaning of lvl?
Link to the code that you shared — LINK
lvlis the level of a vertex (or depth, or distance from the root using only span-edges). Visually:It can be used to check if a given back-edge goes up or down from the currnet vertex. In the code you link, I also use it as a marker of "have I already visited this vertex": if
lvl[u]is 0, then it is unvisited by the DFS.Thanks for the description, I realized it after posting it. I have another question if you don't mind, how would we get the list of articulation points?
Observe, the nodes that connect the articulation bridges are the articulation points because if you remove these nodes, then the articulation bridge will be removed and the graph will be disconnected. So, it is ensured that for the i'th node, if dp[i] = 0, then it is an articulation point along with its parent.
Thanks for that. I initially thought that if the
dp[i] = 0, then the vertexishould be an articulation point. However, I did not think that the parent can also be the articulation point, as it is also the part of the bridge. Thanks for pointing out!This is not true. At least, this doesn't give all articulation points. There are graphs which have no bridges but do have articulation points (imagine two cycles which join at one point).
Then what should be the best way to find all articulation point using DFS tree , if we can't use bridges ?
Instead of checking if any one of the subtrees have a back edge passing over u -> v, we should check if all subtrees of that vertex has a backedge.
Because when we remove a vertex v instead of an edge, all the edges connected to that vertex will be gone. So there should be back edges from all the children of v, so as to keep the graph connected.
In conclusion, if any vertex has even 1 subtree without any backedge, its an articulation point.I can give you with the implementation if you want. But you should try it once. Also don't forget to check root vertex as its a special case.
Can you provide DP relation of this? Which do not include low and high time?
We can use the same dp relation
dp[u]= (# of back-edges going up from u)−(# of back-edges going down from u)+∑dp[v] v is a child of uWhile calculating ∑dp[v], if any one of the dp[i] is zero, then the current vertex is articulation point.
That is for any vertex u, all its dp[children] should have non zero value for it to be not an articulation point.
Bro it gave wrong answer .
Deleted
Hello -is-this-fft-, Please excuse the inconvenice that I maybe causing to you.
Can you/Someone please explain me how does the dp[u]'s value equating to zero makes us decide that the edge between u and it's parent is a bridge and I also think that this confusion(lack of understanding on my part) is because I am unable to understand how does this dp[u] helps us in deciding wether or not there is a backedge passing over uv as said in the editorial ? Can someone please solve my doubt and enlighten me, I have been scratching my head for the past 2 days on this editorial and I really want to learn this technique which seems more pure and intuitive as the author says.
$$$\mathrm{dp}[u]$$$ is the number of back-edges passing over $$$up$$$ (where $$$p$$$ is the parent of $$$u$$$) by definition. So of course knowing $$$\mathrm{dp}[u]$$$ helps us know how many back-edges pass over $$$up$$$. Perhaps you are confused about how it is calculated?
If you remove $$$up$$$ and there is no back-edge passing over it, then $$$u$$$ and $$$p$$$ will be in different connected components. If there is a back-edge passing over it then they will be in the same connected component because the back-edge will "hold the graph together".
Actually, bridges can be found with only one additional int and one bool per vertex. They can even be packed into one int occupying different bits.
All you need is classical low array plus a flag if low[v] was decreased at least once. I made a submission to showcase it: 56639790, components_dfs function.
Problem 1: 118E - Bertown roads
Problem: Link
Problem 2 : step 2 — if it is given that graph is vertex cactus in code line 10 — inside if condition , is it necessary to check (there is no back-edge going down from v)? because vertex v can't be the part of two cycles.
Yes, It is necessary. When you have backtracked to the vertex before you enter the cycle, you need to terminate that cycle.
When have you reached the start of a cycle? It is precisely when there is a back-edge going down from that vertex. So if a child of $$$u$$$ in the DFS tree, say $$$v$$$, is part of a cycle and there is a back-edge down from $$$v$$$, then $$$u$$$ is not part of the same cycle.
(Please correct me if I'm wrong)
thanks, i got it. i mistakenly considered it back-edge from u but it is from v.
Finding bridges (or articulation points)When I read your blog the first time I got confused by the heading as if articulation point and bridges are the same things and surely they are not so I think you should change the heading of this section(just a suggestion). Also in the section below this heading you are calculating bridges only.If i am wrong please correct.
One of the best blogs I have ever read this year. Must use this as resources if I continue my teaching in Hanoi CS Olympiad team next year.
1259E - Two Fairs
I am unable to submit a solution for Two Fairs problem. Any suggestion on how can I check my solution is right or wrong. Found it thanks
try this 1277E - Two Fairs
962F - Simple Cycles Edges
how to solve it ..can you give some idea..
How to calculate the number of back edges for every edge? Actually I want to know whether it is possible to calculate the minimum number of edges needed to remove from the graph to make this edge a BRIDGE in a reasonable time limit if it asks for several queries.
Store it in a dp, and simply add each child's dp contribution to its own dp.
Something like dp[node] = sum(dp( [ children ] ) + backedges_from_current node
Not exactly this (but the main idea is same), you'll have to modify the DP so that the contribution is reflected in all the edges falling in the range of backedge.
Take a look at my solution. (dfs2( ) calculates the exact same dp what you've asked for)
Can be done in a single DFS
Thanks for the comment.
Let me clear, what do you mean by dp[node]? how it handles the answer for an edge ?
Ohh, I should've explained that.
Basically, dp[node] stores the answer for the direct edge coming to the node from its parent. Also, I believe that the answer will be the same for even the back edge from that particular node (haven't concretely proved it though).
Check out the DFS tree (given in the blog), and it'll be a lot more clear then.
This is not true always that dp[node] will store the minimum number of edges needed to remove from the graph to make the edge (parent -> node) a BRIDGE. I can give you an example of a graph. let's consider the graph given below:
8 12
1 2
1 3
2 3
2 4
2 5
3 5
3 6
3 7
5 8
6 8
6 7
7 8
Check out the DFS tree, I repeat "DFS tree" of the graph.
Here take a look at my solution, where I use the exact same transformation.
I edited my first comment to be more clear.
It is the same as the (+1, -1) trick used in array range update.
Take a look
In the problem, "Removing edges to form a Bipartite", are we supposed to minimize the number of edges removed..? If not, Why don't we just remove all the back edges, by which we will be left with just the spanning tree, which can be easily shown bipartite...?!
The problem said that you just have to remove exactly one edge from the graph to make it bipartite.
Nice tutorial. Please, make tutorial on DOMINATOR tree of directed graph.
Thank you -is-this-fft- for the amazing tutorial, waiting for the Dominator tree of Digraph tutorial.
Very nice tutorial -is-this-fft- I have been trying to understand bridges from quiet some time, This post makes it very clear, Thank you very much
One question, Can you give some sample code to calculate articulation points as well
I understand if there is a bridge we can add child and parent to articulation points given that child is not a leaf node of dfs tree, But those does not include articulation points like in the following image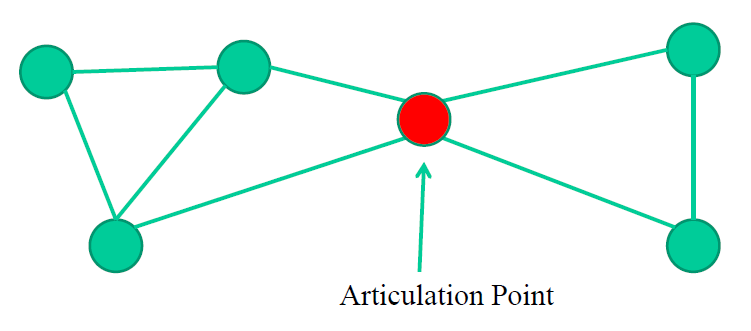
Once again, This is very good stuff to picturize bridges, Thank you
Not being explicit about articulation points was kind of intentional. I think if one understands the part about bridges then they can derive the articulation point part on their own, and this way the reader will be forced to make sure they understand.
Anyway here is the first step on how to find an articulation point.
A vertex is not an articulation point if and only if an edge passes over it from each of its subtrees. (Notice that according to this, the leaves of the DFS-tree are not articulation points.) The root of the tree is a special case: it is an articulation point if and only if it has more than one child.
A vertex can be an articulation point even if there exists a back-edge going over it if it has multiple children and only some children's subtrees have back-edges that go over it while others don't.
Yeah, you're totally right! I wrote that comment in a hurry and didn't think it through. I have edited it now.
"A vertex is not an articulation point if and only if an edge passes over it from each of its subtrees."- That back-edge should also not go down from the vertex to its subtree, right?
No, if for some subtree it only goes down from $$$u$$$ but not from above $$$u$$$, then $$$u$$$ is an articulation point (root is a special case here).
Yeah. So, it means that if u is an articulation point (excluding the root) then there must be at least 1 child v of u such that u-v is a span edge and dp[v] — count(back-edges down from u passing over span edge u-v) = 0
This "dp" is the same you have used for finding bridges.
Please let me know if the condition is correct or not.
Could you provide an implementation of finding articulation points? I got the idea but feel it's hard to do without additional arrays. Thank you!
its now ok
As said by -is-this-fft- ,
A vertex is not an articulation point if and only if an edge passes over it from each of its subtrees.And hence we cannot simply calculate dp[u] and come to the conclusion whether u is an articulation point or not. We have to check for each of its children.
See this diagram
Let c1 and c2 are the two children of the vertex u. They are also the roots of the subtree from c1,c2... Pu is the parent of u or any other nodes which are ancestors of u.
As said in the blog,
I define dp[u] as the number of back-edges passing over the edge between u and its parent.Similarly, dp[c] is the number of back-edges "passing over" c and its parent(i.e u). Now, dp[c] consists of 3 kinds of back-edges(shown with color red in the diagram):-
These back-edges can be considered as ropes where the entire subtree rooted at c is hanging from Pu EXCEPT the one that ends at u because we would loose this edge as soon as we remove the vertex u. Let's call them bad edges .So we have to substract such bad edges from dp[c]
After doing all these calculation , if for any child node c , dp[c] ==0 then u is an articulation point because there is no rope that holds the subtree rooted at c from Pu and would therefore form a separate component...
Here is the implementation of the above logic. I tested it with some standard examples and its giving the correct answer. ...
In the diagram shown above 1,2,3 represents the edges from u. Its quite obvious that in the DFS traversal it would always go from 1-> 2 -> 3 and NOT from 1->3->2. Hence whenever it goes to a subtree it had already visited the bad edges from the previous subtree. This makes the implementation a lot easier
Your code failed the last test in Necessary Cities, changing line 67 to
if (x > 0) continue;gave ACHere's a short articulation points implementation for future visitors (It got AC on cses):
Can someone give a basic idea on how to solve this problem: 101612G — Grand Test?
How to solve the question as I'm unable to get any solution from the crucial points?
Find three disjoint paths (except for the start and the finish) = find two overlapping cycles = find a span-edge $$$uv$$$ such that at least 2 different back-edges pass over it.
Thanks for the help. Finally solved it.
JacobianDet Can you explain your solution? Are there any restrictions for the back-edges ?
No restrictions, there are checks which you need to write for getting the requirement
I feel the crucial point is the first observation
The back-edges of the graph all connect a vertex with its descendant in the spanning tree.
The explanation helped a lot. Thanks.
https://codeforces.com/contest/1364/problem/D
A new problem that can be solved by getting a cycle that doesn't have any edges "cutting through it." use back-edge.
old problem : 1325F - Ehab's Last Theorem
I read this ages back and liked the sound of it but only just used it to make a problem's implementation much nicer:
1045C - Hyperspace Highways
Create the DFS tree then for each query do LCA and then greedily take the longest paths upwards from vertices a,b to the LCA. If we overshoot the LCA, then we could have reached it anyway due to the special cycle property of the graphs
can someone give pseudocode/code to create a dfs spanning tree and to check for articulation points?
If you are okay with learning how lowlink works, here's a good video about it from Matt Fontaine that explains how, with a live coding demo at the end.
You can try this
This is pure gold!
24 Caret Pure
me after reading the blog: "-is-this-dfs-"
There's a really nice solution of 406C - Graph Cutting described by scott_wu here https://codeforces.com/blog/entry/11186?#comment-162599 .
I think this solution is much more understandable than the editorial solution, and the DFS tree is what makes the solution so clear.
-is-this-fft- I feel dumb asking this. In the implementation to find Bridges.
// in dfs
if (visited[to]) { low[v] = min(low[v], tin[to]); }
Why can't we do low[v] = min(low[v],low[to]) or both things are different?
Got it. This is because the back edge vertex can be an articulation point. So, if we do low[v] = min(low[v],low[to]) then it will connect both of the components.
see Example
7 8
1 2
1 3
2 4
3 4
4 5
4 6
5 7
6 7
I think the low[v] = min(low[v], low[to]) should hold good for the bridges but not for the articulation points. Isn't it? I tried this for finding bridges a long time ago and it worked well. It's just that it doesn't work well for articulation points.
The sad part is that I can only give you upvote for this amazing article.
p.s this is the best blog I have read on cf.
ILY
Hello, -is-this-fft- in the Why? section of Observation 1, I think that there will be the following correction
Thus it was explored while exploring one of the other neighbours of u, which means that v is a
descendantancestor of u in the DFS tree.Please correct me If I am wrong and if possible can anyone explain me this particular line if what is written is not a typo.
No, descendant is correct.
i am unable to clearly understand that line then, can you or someone please explain this line.., it would be a great help
You arrive at $$$u$$$. Its neighbor $$$v$$$ is still unexplored. You start to recursively explore the neighbors of $$$u$$$ in some order, but when you get to $$$v$$$ it is already explored. Recall that it was unexplored when we got to $$$v$$$. Therefore, we explored it while exploring one of $$$u$$$'s other children, let's call it $$$w$$$. Because we explored $$$v$$$ while exploring $$$w$$$, $$$v$$$ must be in the subtree of $$$w$$$ and thus also $$$u$$$. Therefore $$$v$$$ is a descendant of $$$u$$$.
It is easier to detect back edge in undirected graph by comparing levels, but how to detect in directed graph?
that is called
detecting strongly connected componentsIn a directed DFS tree, you have 4 types of edges:
The advantage/simplification here is that there are no right-edges. Both up-edges and left-edges can be thought of as "back-edges" in some way. To detect, you can find for every vertex $$$\mathrm{ord}[u]$$$, the time at which it was first found in the DFS. An edge $$$u \to v$$$ is then a up- or left-edge iff $$$\mathrm{ord}[v] < \mathrm{ord}[u]$$$. To detect which, you have to check if $$$v$$$ is an ancestor of $$$u$$$. This can be done by also storing for each vertex the last time it was explored in the DFS.
Sir, -is-this-fft- while calculating the dp[u] we are are adding dp[v] where v is a child of u.
how can i convince myself that the backedges from its child also passes over "up" where p is the parent and u is the node.
Please help.
You subtract the ones that don't in the "back-edges going down from $$$u$$$" part.
An example problem for Problem 3: 1680F - Lenient Vertex Cover
Amazing blogpost!
dp[u]=(# of back-edges going up from u)−(# of back-edges going down from u)+∑dp[v] v is a child of u.
i still dont understand this formula, why are we subtracting number of back edges going down from u ?
when you add dp[v] to the dp[u], you add all the edges going up from v, this include the edges that go up from v and continue to go up from u, this contribute to the answer, however there are edges in dp[v] that starts at v and end at u, this is included in dp[v] from definition but we need to omit these edges as these are not back edges going up from u, hence we explicitly subtract all edges going down from u
Hi, -is-this-fft-
I was trying to solve this problem using the DFS tree. I already came up with a solution, which involves compressing the graph into bi-connected components. Although I already know how to find bridges and articulation points using the DFS tree, I don't know how to compress the graph.
Can you please help?
did you do it? and how?
How can such a masterpiece exist?
Very Nice Blog. I may come back here later again :)
Does anyone have any materials on how to build the DFS tree itself? Like i know its built using the DFS algorithm but how is it stored during and after using DFS on a graph? If anyone can provide specific material or comment about this it would be nice thank you :))) also sorry for posting so late i couldn't find many other places about the dfs tree