I once read a paper that claimed and used the fact that the Hungarian algorithm can be implemented in such a way that it runs in $$$O(m n \log n)$$$ time. Using the soft-O notation which ignores log factors, the complexity can be written as $$$\tilde{O} (m n)$$$. If the graph is dense, i.e. $$$m = \Theta(n^2)$$$, the log factor can be removed There are many tutorials on how to get $$$O(n^3)$$$, but I couldn't find any references that directly show how to do $$$\tilde{O}(mn)$$$ from end to end (but I found just enough to conclude that it is probably possible). So I decided to write one up myself and well, this is as good a place as any.
In my last blog, I showed how thinking in terms of linear programming and duality can be useful when working with maximum flows and minimum cuts. The usefulness of this is best demonstrated with examples, and this is a good example. In fact, this is pretty much the primal-dual algorithm: it was one of the prototypes that inspired the entire theory. So, this should in fact be an excellent example to gain more intuition of the concept.
As I said, this algorithm makes a nice case study of linear programming and duality. It also brings together many other ideas, so this is a learning opportunity for many things.
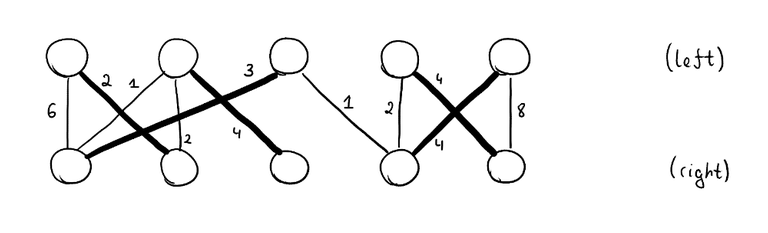
Problem statement
You are given a bipartite graph with $$$n$$$ vertices and $$$m$$$ edges. Each edge has a cost $$$c_e$$$. You want to find the minimum cost perfect matching: each vertex on the left must be matched to exactly one vertex in the right and vice versa. The sum of the costs of the edges that are in the matching must be minimized. We assume that at least one perfect matching always exists.