Hello everyone. The question goes as follows : Given an unweighted undirected connected graph we need to construct the tree with minimum depth such that the tree consists of all the vertices of the graph. Any thoughts about the approach? Thank you in advance :).
Please subscribe to the official Codeforces channel in Telegram via the link https://t.me/codeforces_official.
×
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 9 | TheScrasse | 144 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/22/2024 10:21:06 (g1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











bfs with leaves as source?
Can you elaborate on your solution?
We can find leaves as nodes with degree == 1. Running bfs with leaves as sources gives us a bottom up traversal of the required tree. So, the last node to get popped out of the bfs queue is a possible root.
Once we've found the root, we just need to print or return the tree in required format.
The given graph is a general graph and might not have nodes with degree of 1?
I assumed it was a tree from the beginning which was not specified. In this case, my solution doesn't work.
If it was a tree from the beginning then wouldn't the construction just be the tree?
Depth still needs to be minimized
Then just find centers?
Since bfs level of all sources is 0, all leaves have equal level. Since this is bottom up traversal of required tree, all leaves have same height == level == 0.
By taking the last node in bfs queue as root, we ensure that it is equidistant from all leaves and thus has minimum depth.
In general, computing a dfs tree of minimum depth in a graph is np-complete. See here. Are there any additional constraints given in the problem that would make the construction of the minimum depth tree optimizable?
We can consider the graph as connected. If it is connected we can run bfs from each node of the graph to find the depth of the tree when that node is considered as the root. We can keep track of the minimum depth and root which gives the minimum height. Am i missing something?
Yeah youre right I think I just misread something — does the problem require better than O(N^2)?
This problem is clearly a complication of the problem asking for the length of the diameter (the length of the diameter is either
2 * minimum_deptheither2 * minimum_depth - 1).The diameter problem can't be solved in a general graph with a better complexity than
O(n^2)(the 2-bfs algorithm only works in Trees).For finding the path of the diameter, simply start a BFS from each node, while storing where you came from for being able to reconstruct the path.
The answer of the problem can't be smaller than the length of the diameter / 2, so choosing the middle node of the diameter as a root and creating the tree by using the edges used when making a BFS from it is an optimal solution.
Thank you for the clarification. What do you think about .Hello solution?
It fails a few cases :( The simplest one i found is this one: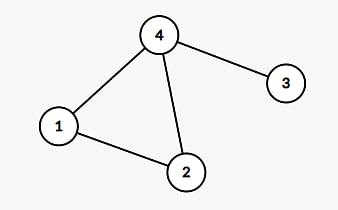
The answer is 1: choose
4as the root.Now using the single BFS solution: Let's say that we started the BFS from 1. We obtain the following spanning tree:
Any root we choose will give an answer of 2.
Hey, what is n in your asymptotic? I do not think it is possible to do in n ^ 2 if n is a number of vertices. It's always better to use V and E with vertices and edges respectively. Don't mislead people. I believe that the way you proposed runs in O(VE) (we run BFS that runs in O(V + E) = O(E) V times) which is O(V ^ 3) if E = O(V ^ 2). And, you said a wrong statement that in can`t be solved faster without even googling some information on this topic! There is an algorithm that has a better asymptotic: link. Of course, it is not practical at all, because it uses Coppersmith–Winograd algorithm for matrix exponentiation, but, still, you were too arrogant to say that it can't be solved with a better complexity than O(n ^ 2) (even though you obviously meant O(VE)).
Typically V is roughly equal to E, otherwise you would have to store an absolutely mind-boggling number of edges. Saying it is O(n^2) is perfectly acceptable to me. And you can't actually say that this random algorithm you googled is faster, considering it is roughly n^2.561 for integer weights, and does not rely on the number of edges.
Well, he's right. It can't, at least not yet, according to the paper you linked.
Typically V is roughly equal to E, otherwise you would have to store an absolutely mind-boggling number of edges— this is one of the most stupid things i've ever heard, and it's actually extremely weird to hear such thing from a yellow guy. Why do people need such thing as adjacency matrixes, if "Typically V is roughly equal to E"? Why do we need Floyd-Warshal algorithm? It's absolutely wrong.As for the second statement, he clearly meant O(VE) as this what his algorithm does: V times runs bfs in O(V + E). Finally, i don't say that this algorithm is faster in practice (in fact, it's hundreds time slower), but it`s clearly has a better asymptotic for general graph (on average in random graph E = O(V ^ 2)), but it is worse for sparse ones. As for your saying, that it depends on integer weights, that's ok, as the graph is unweighted (see the problem statement in the blog), so it is in fact asymptotically faster for general graphs.
And after i thought on it for a while, i released, that we can use the knowledge that the graph is unweighted in the other way. We can build bitset adjacency matrix and do the bfs on this graph using bitset in O(V ^ 2 / w) (we build a matrix onece, and that we V times run O(V ^ 2 / w) algorithm so the overall complexity is O(V ^ 2 + V ^ 3 / w), where is w is the length of a machine world, typically w = 64. Not only does it have a better complexity, but also it will be fast in practice: here we don't have many cache misses and bitset will work fine, i think about 30 times faster at least, as we don't have to store the queue explicitly (in general bfs, there are quite a lot of cache misses).
When saying that V is typically roughly equal to E, he meant not in a random graph but about 99% of graphs on cf problems.
This sounds like the exact same algorithm the original guy posted. How will bitset improve the complexity?