Couldn't see the full ranklist.
Idea on B, E, G, J, K, L?
Got tle in G using sqrt decomposition on the height.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
| Name |
|---|



B: let $$$v$$$ be the vertex on path from $$$a$$$ to $$$b$$$ that is closest to $$$c$$$ and let $$$u$$$ be the vertex on path from $$$c$$$ to $$$d$$$ that is closest to $$$a$$$. Then first we move either $$$a$$$ or $$$b$$$ to $$$v$$$, then from $$$v$$$ go to $$$u$$$, then go to $$$(c, d)$$$. The second part is obvious and the last part it symmetric to first, so now we only need to solve the first part. Root the tree at $$$v$$$. Go from $$$a$$$ to the deepest leaf in its subtree or until $$$b$$$ becomes equal to $$$v$$$. Then do the same for $$$b$$$. Do that until you reach $$$v$$$. If the depth of subtree of $$$a$$$ doesn't increase, then the answer is -1.
G:
Since the array is random the number of segments with different minimum and maximum is $$$O(n \cdot log)$$$. Compute segments with equal minimum and maximum. Now, each query is equivalent to number of points in a rectangle.
B: Find a point $$$root$$$ so that the worm the starting position lies entirely in some subtree of it and the final position has no node in this subtree. Now it is easy to see that at some point the worm has to move to some path that starts at $$$root$$$ and ends somewhere in the subtree, then directly moves to a point that starts at $$$root$$$ and ends somewhere in another subtree, and finally moves to its destination. The first and last parts can be done greedily. You choose one end, go as deep as possible from there, then go as deep as possible from the other end, etc. until the other end can move directly to the $$$root$$$. You can try both options of which end goes deeper first and keep the best one.
L: The center of the donut is center of mass of all points. If it's not integer, answer is "NIE". To get $$$R$$$ store the leftest point in the set. For each radius $$$r$$$ precalc number of points in the circle of this radius $$$cnt_r$$$ and hash of such circle $$$h_r$$$ (if you move the center of the circle, you just need to multiply hash by some power of $$$x$$$). Now we need $$$cnt_R - cnt_L = n$$$, so you can find $$$L$$$ from this equation. Now all that remains is to check that hash of all points is equal to $$$(h_R - h_L)x^{shift}$$$.
Instead of hashing you can also compare the actual and the expected value of $$$\sum(x[i]-a)^2+(y[i]-b)^2$$$ and then make sure that there are no points outside the outer circle. For this last check, you can remember $$$ymn$$$ and $$$ymx$$$ for each value of $$$x$$$ and iterate over $$$x$$$ to check it. Because this is the last check and there won't be many times when we pass all other checks, so the extra running time of this check wont hurt.
E: I haven't implemented it yet, but I think the following should work. First, for each segment determine the time it first breaks. To do this, classify the drones as heavy or light (a drone is heavy if it has more than something like $$$sqrt(k)$$$ changes in height). Then for edges connecting two light nodes or two heavy nodes we can merge-sort-like compute the breaking time, for edges connecting a light node to a heavy node we can iterate over changing times of the light node and use range queries on the changing times of the heavy node to compute the breaking time. From this it is relatively easy to calculate the answers for the queries using DSU and either parallel binary search or some small-to-large merging.
Instead of splitting vertices, you can just solve for all edges for min degree vertex. It would be ksqrt(E) on general graph, And 5k on planar, like in the problem. One phrase in input format is good place to say about planarity, isn't it?
how does it help that it's planar?
If degrees of all vertices are $$$\geq 6$$$ it means that $$$2E \geq 6V$$$, it means that $$$E \geq 3V$$$, but by Euler formula, we know that $$$E \leq 3V-6$$$.
It means that in any planar graph exists a vertex with a degree at most $$$5$$$.
If you will delete this vertex and all edges outgoing from it, the remaining graph will be planar too.
Using an algorithm like "pick vertex with the smallest degree, delete from the graph, change degrees of adjacent vertices" you can find the orientation of edges with outgoing degrees $$$\geq 5$$$.
Thank you very much!
On the contest I indeed computed the degeneracy order leading to having an orientation with outdegree <=5, but then I completely removed it and replaced it with "direct edge from one with smaller number of updates to one with bigger number" which is much simpler and provides the best orientation xd.
Originally this was written in the main part of the statement (not the input format section), and it was written in bold (and that was the only bolded thing). But I haven't seen the translation, maybe the bolding was removed in the process.
I did the translation, and as far as I know, it remained in bold, right in the middle of the statement. Not sure how anyone could miss it.
L: The center's coordinates $$$(a, b)$$$ must be the average $$$x$$$ and $$$y$$$ coordinate of all points, respectively. Also, the outer radius $$$r$$$ will be $$$max(x_i) - a$$$. Knowing $$$r$$$ and $$$n$$$ we can deduce the inner radius $$$l$$$ by pre-computing $$$count[x]$$$ = number of lattice points in a circle of radius $$$x$$$. Now we have to check if the donut $$$(a, b, l, r)$$$ matches the current set of points. To do that, one can assign point $$$(x, y)$$$ a value of $$$p^{x}*q^{y}$$$ for some $$$p, q$$$ and maintain the sum modulo some big prime. Note that translating the center from $$$(0, 0)$$$ to $$$(a, b)$$$ multiplies the value by $$$p^{a}*q^{b}$$$, so to get the value of a certain donut one can also pre-compute the values of each circle of radius $$$x$$$.
G: Important observation: because books heights are random, the length of the longest increasing sequence starting from some book will be small (something in the order of $$$log(n)$$$) with high probability. We will process the queries offline in decreasing order of $$$l[i]$$$ and keep the number of fragments for each value of $$$r[i]$$$ in a segment tree. When we decrease the current value of $$$l$$$, new books become available and we have to update the segment tree. Because of the observation, this updating can be done fast.
K: I haven't implented it yet, but I think the following should work. First for x and y independently, calculate the points in the (t,x) and (t,y) plane that contains all paintings. This can be done with half-plane-intersection. Then from this we will get piecewise linear functions for the amount of overlap of all paintings in the x-dimension and in the y-dimension. We can combine these functions to calculate a piecewise quadratic function for the area of the overlap of all paintings. On each piece, calculate the maximum of that piece, split the pieces there and in the query points, and then the answers to the queries become simple range maxima.
That's correct. Even more, it turns out that the main function is bitonic. So either that global maximum is the answer or value at L or R.
How to prove it?
It isn't trivial to prove.
Function for $$$x$$$ is concave (and bitonic) and piecewise linear, same for $$$y$$$. While both functions are increasing, the product increases too. Then one of two functions starts to decrease and the product is piecewise quadratic (each piece is concave parabola). Let's consider the first moment when the product is decreasing. We have a peak of some parabola that came, say, from product of $$$(-x + 3) \cdot (2x - 4)$$$. If we continued with this formula to the right, the function would still be decreasing. And the thing is that the two functions are concave, so on the right (for next linear pieces) we can only have smaller values so we will be even below that parabola.
the fact that f(x) <= parabola doesn't mean that it will be bitonic/concave.
Note also that when both x and y will become decreasing, their product will be piecewise convex(positive t^2 coefficient), that is certainly not concave (maybe still bitonic)
UPD: just understood that you didn't claim that and we don't care about that. We only care that global max is unique which you proved
No, we actually need bitonicity and I don't understand your proof again.
If x and y were twice differentiable we could say that while x(t), y(t) are both increasing xy increases, when both are decreasing xy decreases, and when one of them is decreasing and other in decreasing $$$(xy)' ' = x' 'y + 2x'y' + xy' '$$$ where all of the summand are negative because $$$x' ', y' ' < 0, x > 0, y > 0, x' y' < 0$$$'. It seems it should generalize to any concave functions (but I do not actually know how to do that)
I claim that the product is bitonic but not necessarily concave. The two functions are concave though.
OK, I figured that it's what are you claiming but I didn't quite get the argument
The idea is: there is a peak where the product decreases for the first time. Then it would decrease as a parabola but actually it decreases even more.
============================================================As a more formal proof, one can consider these two functions as ordinary concave differentiable functions on some interval (despite these functions are not differentiable at bending points, it doesn't matter a lot; and on the other hand the statement must hold without the piecewise linearity property because every (of course adequate, like in $$$C_1$$$) function can be approximated) $$$f$$$ and $$$g$$$ where $$$f(x)$$$ and $$$g(x)$$$ are positive for all points from $$$I$$$. Let $$$x_1$$$ be (any) peak point of $$$f$$$, $$$x_2$$$ be (any) peak point of $$$g$$$, $$$x_1 < x_2$$$. Then of course $$$f\cdot g$$$ is increasing before $$$x_1$$$ and decreasing after $$$x_2$$$. On $$$(x_1, x_2)$$$ one can see that $$$f(x)$$$ is decreasing, $$$g(x)$$$ is increasing, $$$f'(x)$$$ is negative and decreasing, $$$g'(x)$$$ is positive and decreasing, so $$$f(x)/g(x)$$$ is positive and decreasing, $$$f'(x)/g'(x)$$$ is negative and decreasing, so $$$f(x)g'(x) + f'(x)g(x) = (fg)'(x)$$$ is decreasing, which exactly means the bitonicity of the product.
What about F?
For each index $$$i > k$$$, we have $$$A_i - A_{i - k} = S_{i - k + 1} - S_{i - k}$$$. So we can express every element as $$$A_j + constant$$$ , where $$$1 \le j \le k$$$.
Now for each $$$1 \le j \le k$$$, we know the relative positions of elements. Since in the end the elements form a permutation of $$$1$$$ to $$$n$$$, you know that the smallest element of one of these will be $$$1$$$, then the smallest element of another will be the smallest unused and so on.
In this way, you can try all $$$k!$$$ permutations.
It looks almost exactly as my editorial :P
Where can we find editorial?
It will be published soon, but it is in Polish :/
But how can I find where element 1(for example) need to be in a row of relative positions?
It will have to be the smallest one, because otherwise you will need something smaller than 1 for the smallest.
Can problem I be solved faster than $$$O(n*log(n))$$$? Our solution got TLEd and we had to make shitty constant optimizations...
I am aware that our solution involved duplicating the string, so I'd also be glad to know if it can be done without doing that.
Did you use cin/cout? It seems to run 10+ seconds slower than scanf/printf...
You can notice that 2 first letters determine rest of the string. So you can check all possibilities and run manacher on it.
Oh wow, daily reminder that I'm actually getting dumber as years pass...
Don't be so harsh on yourself, many good contestants (including us) didn't figure it out xd
Can you describe solution without this observation?
Ummm, I was not the one to solve it in my team, so I am not really familiar with the solution, but there was kinda similar problem on Polish OI where we are given some information about some pairs of equal substring and we need to determine number of strings satisfying this or something like this (which was identical problem to one from fifth contest of Petrozavodsk Winter 2016). Many contestants thought about it in these terms and did something similar to solution of this problem.
My guess is that this is the problem you're talking about.
We also knew about the problem and went down that route and lost a lot of time :)
I think the idea comes from this paper Universal Reconstruction of a String.
There is a problem in ONTAK 2010 (Palindromic Equivalence) that don't need the "first two letter" observation and also don't need extra $$$\alpha(n)$$$ or $$$\log(n)$$$ factor.
Anyway, I also didn't have that observation, and when I got TL and found out that the output may grow up to 3.2GB, I just ragequit. (Now I think there was a bug)
We joined the equivalent positions as follows: create $$$2n$$$ vertices, each position $$$0 \leq i < n$$$ is assigned $$$2$$$ vertices $$$i$$$ and $$$Mirror(i) = 2n - 1 - i$$$. Then if $$$l..r$$$ is a palindrome, we join $$$l$$$ with $$$Mirror(r)$$$, $$$l+1$$$ with $$$Mirror(r-1)$$$ and so on. This way we have a bunch of queries of the form "join $$$a+i$$$ with $$$b+i$$$ for all $$$0 \leq i < k$$$", and have to report the connected components.
To do that, we used modified DSU. First decompose the queries into $$$2$$$ parts so that each of them has length of the form $$$2^k$$$ (as in Sparse Table). Then go from large $$$k$$$ to $$$0$$$. If vertices $$$u$$$ and $$$v$$$ are connected at step $$$k+1$$$, then we join vertices $$$u + 2^k$$$ and $$$v + 2^k$$$ at step $$$k$$$. This is equivalent to joining $$$u + 2^k$$$ and $$$root(u) + 2^k$$$ for each u. After that, for each query $$$(a, b, 2^k)$$$ we join $$$a$$$ and $$$b$$$.
Where can we see the problem set?
Please tell us how to solve problem I?
Does anyone have pictures of standings? It seems I can't access it in any way currently. Just for the record, I + Marcin_smu + mnbvmar did 11 problems (without J) with a really terrible time.
There are results in Yandex Contest now.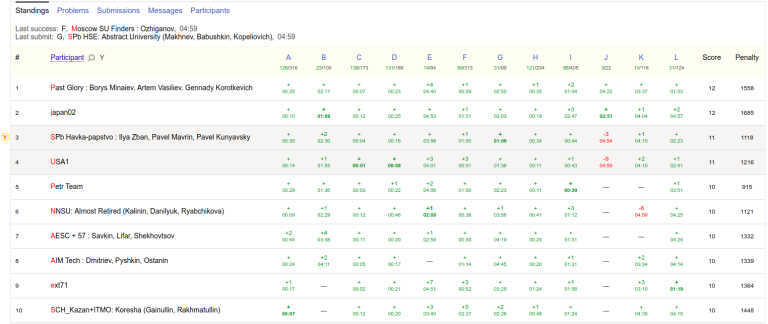
Can somebody share solution for J?
Let's solve an easier problem first. Count the number of lines going through the segment between vertices $$$a$$$ and $$$b$$$. Sort the antennas by angle with respect to $$$a$$$. If you now move $$$a$$$ to $$$b$$$ then two antennas swap their position if and only if the line through them goes through the segment connecting $$$a$$$ and $$$b$$$. To get the number of such lines compare the order of the antennas sorted with respect to $$$a$$$ and sorted with respect to $$$b$$$ and calculate the number of pairs which swapped their position. This can be done in the same way as counting the number of inversions in an array in $$$\mathcal{O}(m\log m)$$$. Now precalculate this number for every pair of $$$a$$$ and $$$b$$$ in $$$\mathcal{O}(n^2m\log m)$$$.
Call the number of lines going through the segment $$$(a,b)$$$ $$$x_{ab}$$$ and the number of lines going through $$$(a,a+1)$$$ and $$$(b,c)$$$ $$$y_{bc}^a$$$. Let's solve the problem for $$$n=3$$$ and then try to generalize the solution for arbitrary $$$n$$$. Obviously the following holds $$$x_{12}+x_{23}-x_{13}=2\cdot y_{23}^1$$$. Therefore we can calculate $$$y_{a+1b}^a$$$ in $$$\mathcal{O}(1)$$$ for any triangle. To generalize this for any convex polygon, notice that $$$y_{a+1b+1}^a=y_{a+1b}^a+y_{bb+1}^a$$$. With this formula we can calculate $$$y_{bb+1}^a$$$ and therefore answer queries in $$$\mathcal{O}(1)$$$. The total complexity is $$$\mathcal{O}(n^2m\log m+q)$$$.
We have just published all the data from AMPPZ (the original Grand Prix of Poland). If anyone is interested, the statements in English are at https://amppz.tcs.uj.edu.pl/2019/data/amppz-en.pdf and the test data can be accessed at http://amppz.tcs.uj.edu.pl/2019/data.html, with only minimal amount of effort of reading Polish. There is also an editorial at https://amppz.tcs.uj.edu.pl/2019/data/amppz-slajdy.pdf, but with significantly more effort needed.
edit: links updated
antontrygubO_o
Can you please turn on 'show tests' mode for upsolving?
Del